Introduction
First of all, this article is best viewed in Chromium and Google Chrome browsers. Some characters are not rendered correctly in Firefox. In this article, some causal effects in the form of $p\left(y|do\left(x\right)\right)$ are calculated for a directed acyclic graph (DAG) from the equivalence class of an image. The rules of do-calculus are going to be used to calculate causal effects. DAGs from the equivalence class of an image have been studied in the articles [1], [2] and [3].
The Causal Effects
Some causal effects are to be calculated for the DAG in the Figure 1. The DAG in the Figure 1 is to be called $G$ from now on in this article.
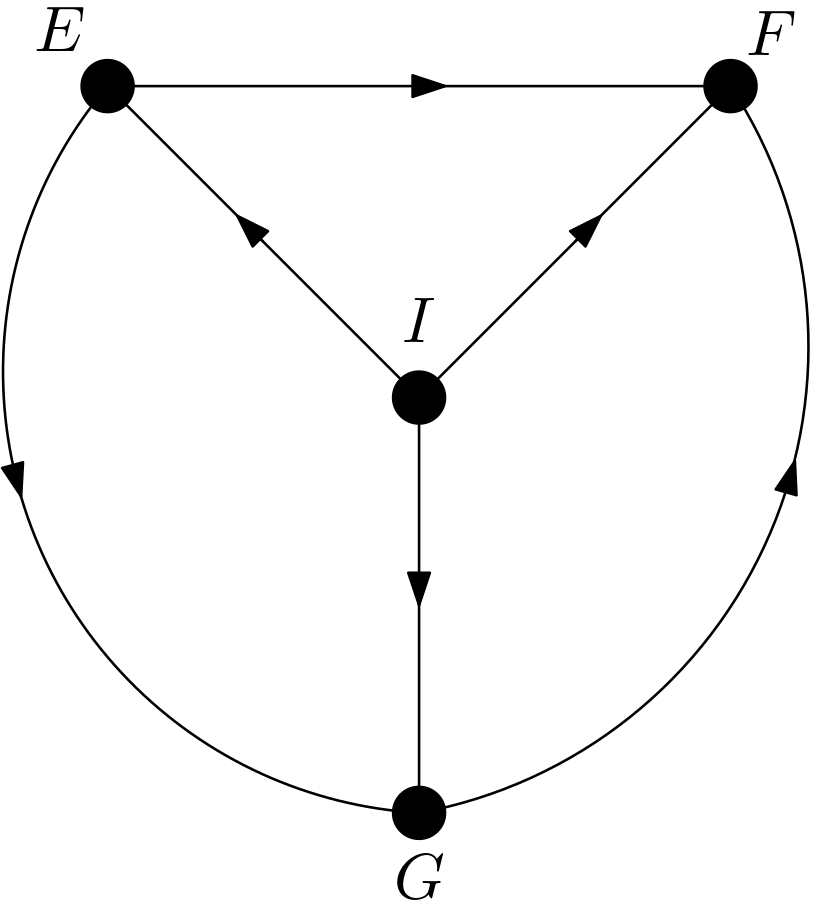
The first causal effect to be studied is $p\left(i|do\left(e\right)\right)$. Can the intervention on $E$ be replaced with observing $E$? Is $p\left(i|do\left(e\right)\right)$ equal to $p\left(i|e\right)$? For this replacement or the equality to be possible, $I$ and $E$ must be d-separated in the DAG $G_{\underline{E}}$. The DAG $G_{\underline{E}}$ is shown in the Figure 2.
$I$ and $E$ are not d-separated in $G_{\underline{E}}$ due to the unblocked path $I \rightarrow E$, which means that $p\left(i|do\left(e\right)\right)$ cannot be written as $p\left(i|e\right)$.
Can the intervention on $E$ be removed? Is $p\left(i|do\left(e\right)\right)$ equal to $p\left(i\right)$? For this removal or equality to be achievable, $I$ and $E$ must be d-separated in $G_{\overline{E}}$. $G_{\overline{E}}$ is displayed in the Figure 3.
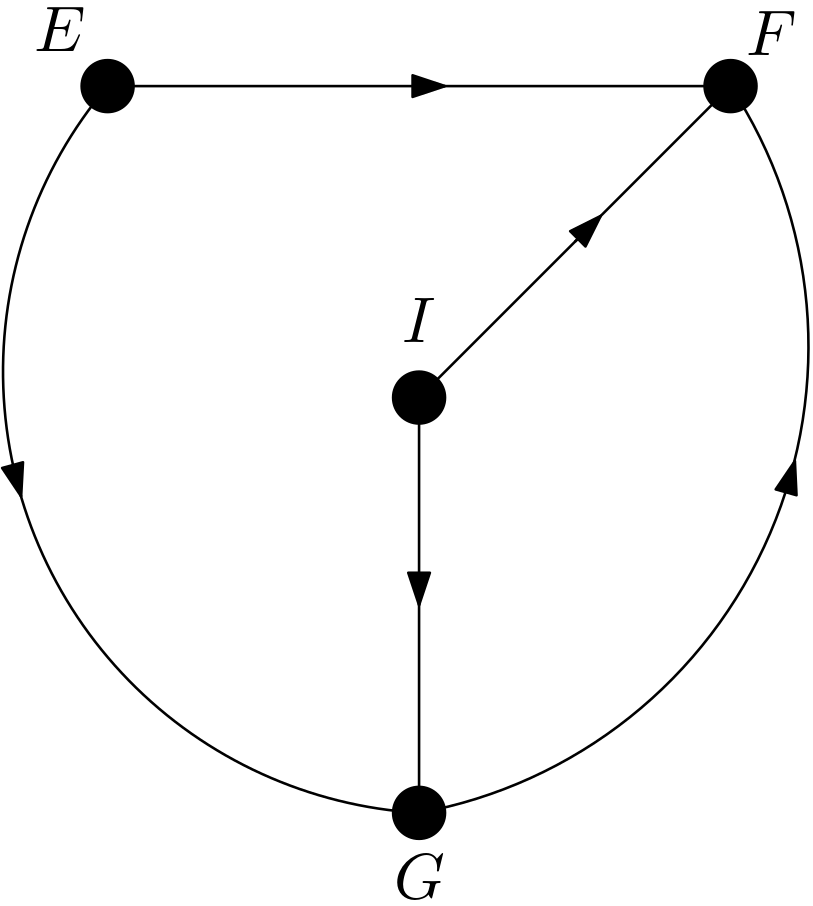
There are four paths between $E$ and $I$ in $G_{\overline{E}}$. They are listed as follows: \begin{equation} \begin{array}{l} 1) \, E \rightarrow G \leftarrow I \newline 2) \, E \rightarrow G \rightarrow F \leftarrow I \newline 3) \, E \rightarrow F \leftarrow I \newline 4) \, E \rightarrow F \leftarrow G \leftarrow I \end{array} \end{equation} The first path is blocked due to its collider structure. The second path is blocked due to the collider $G \rightarrow F \leftarrow I$. The third path is blocked due to its collider structure. The fourth path is blocked due to the collider $E \rightarrow F \leftarrow G$. Therefore, $I$ and $E$ are d-separated in $G_{\overline{E}}$, which means that $p\left(i|do\left(e\right)\right)=p\left(i\right)$. The first causal effect has been shown to satisfy the following equality: \begin{equation} p\left(i|do\left(e\right)\right)=p\left(i\right) \end{equation} The next causal effect to be studied is $p\left(e|do(i)\right)$. Can the intervention on $I$ be replaced with observing $I$? Is $p\left(e|do(i)\right)$ equal to $p\left(e|i\right)$? For this replacement or the equality to be possible, $E$ and $I$ must be d-separated in the graph $G_{\underline{I}}$. The graph $G_{\underline{I}}$ is drawn in the Figure 4.
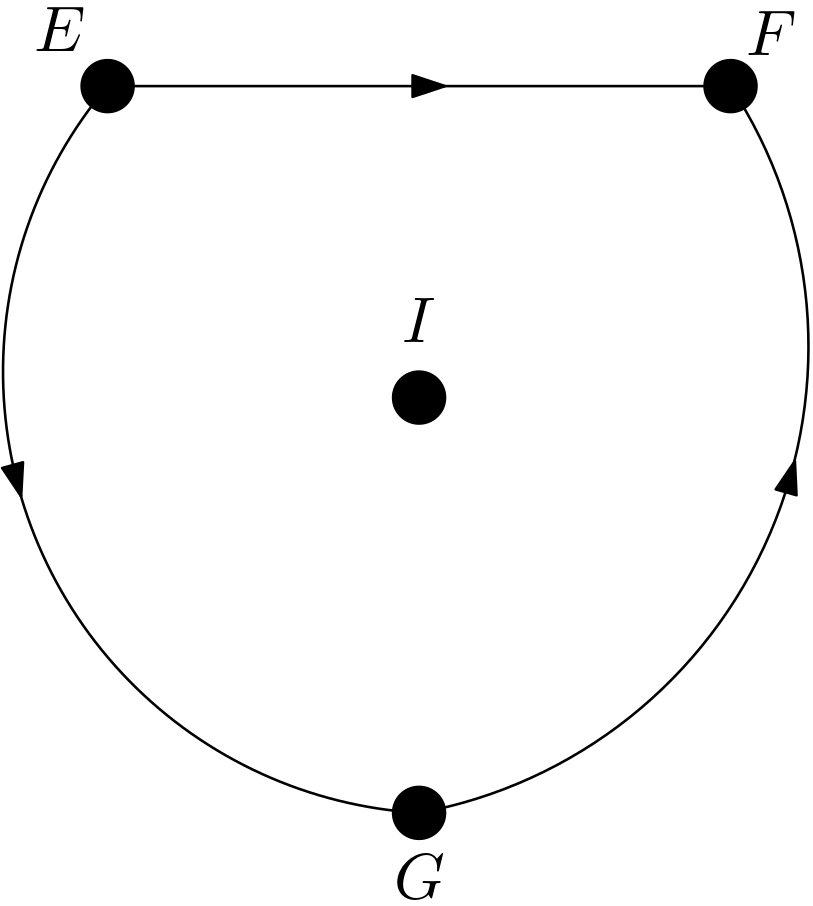
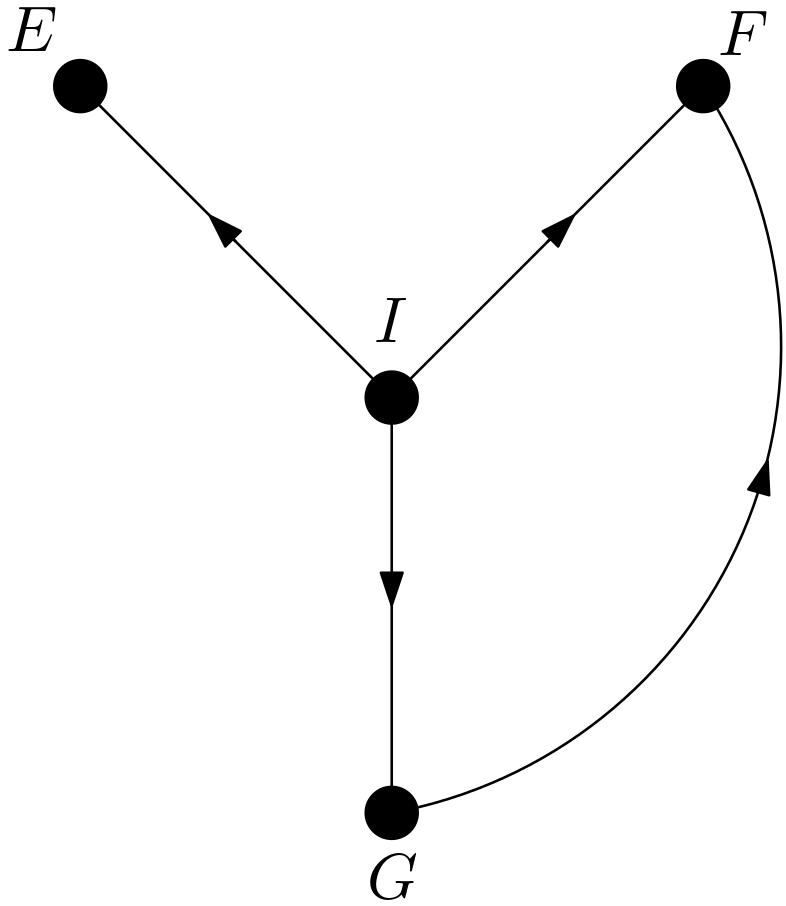
As can easily be detected in the Figure 4, $E$ and $I$ are d-separated. Hence, $p\left(e|do(i)\right)$ can be written as $p\left(e|i\right)$. The second causal effect has been shown to satisfy the following equality: \begin{equation} p\left(e|do(i)\right)=p\left(e|i\right) \end{equation} The next causal effect to be calculated is $p\left(i|do\left(f\right)\right)$. Can the intervention on $F$ be replaced with observing $F$ or is $p\left(i|do\left(f\right)\right)$ equal to $p\left(i|f\right)$? For this replacement or equality to be valid, $I$ and $F$ must be d-separated in the DAG $G_{\underline{F}}$. $G_{\underline{F}}$ is the same as $G$ shown in the Figure 1. From \cite{first_article}, it is known that there are no d-separation implications in $G$. Hence, $I$ and $F$ cannot be d-separated in $G_{\underline{F}}$, which means that $p\left(i|do\left(f\right)\right)$ is not equal to $p\left(i|f\right)$.
Can the intervention on $F$ be removed or is $p\left(i|do\left(f\right)\right)$ equal to $p\left(i\right)$? For this removal or equality to be achievable, $I$ and $F$ must be d-separated in the DAG $G_{\overline{F}}$. $G_{\overline{F}}$ is drawn in the Figure 5.
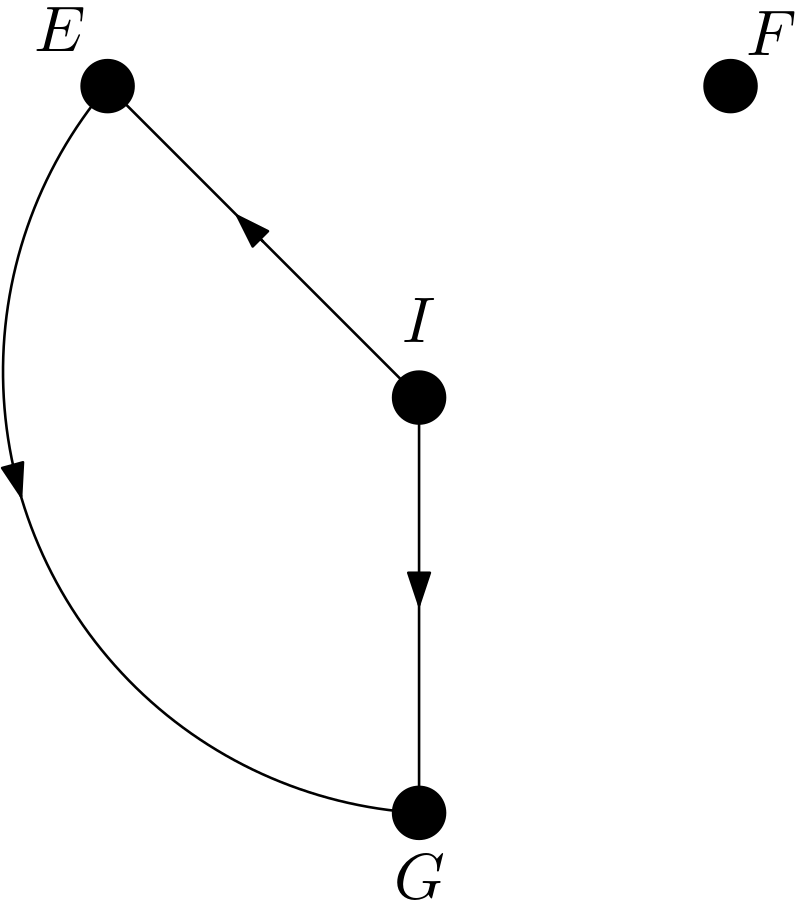
As can easily be observed in the Figure 5, $I$ and $F$ are d-separated in $G_{\overline{F}}$, which means that $p\left(i|do\left(f\right)\right)$ is equal to $p\left(i\right)$. The third causal effect has been shown to satisfy the following equality: \begin{equation} p\left(i|do(f)\right)=p\left(i\right) \end{equation} It is the turn of the causal effect $p\left(f|do\left(i\right)\right)$. Can the intervention on $I$ be replaced with observing $I$ or is $p\left(f|do\left(i\right)\right)$ equal to $p\left(f|i\right)$? For this replacement or equality to be possible, $F$ and $I$ must be d-separated in the DAG $G_{\underline{I}}$. It can be easily seen in the Figure 4 that $F$ and $I$ are d-separated in $G_{\underline{I}}$. Therefore, $p\left(f|do\left(i\right)\right)$ can be written as $p\left(f|i\right)$. The fourth causal effect has been shown to satisfy the following equality: \begin{equation} p\left(f|do\left(i\right)\right)=p\left(f|i\right) \end{equation} The next causal effect to be examined is $p\left(i|do\left(g\right)\right)$. Can the intervention on $G$ be replaced with observing $G$ or is $p\left(i|do\left(g\right)\right)$ equal to $p\left(i|g\right)$? This replacement or the equality is achievable if $I$ and $G$ are d-separated in the DAG $G_{\underline{G}}$. $G_{\underline{G}}$ is given in the Figure 6.
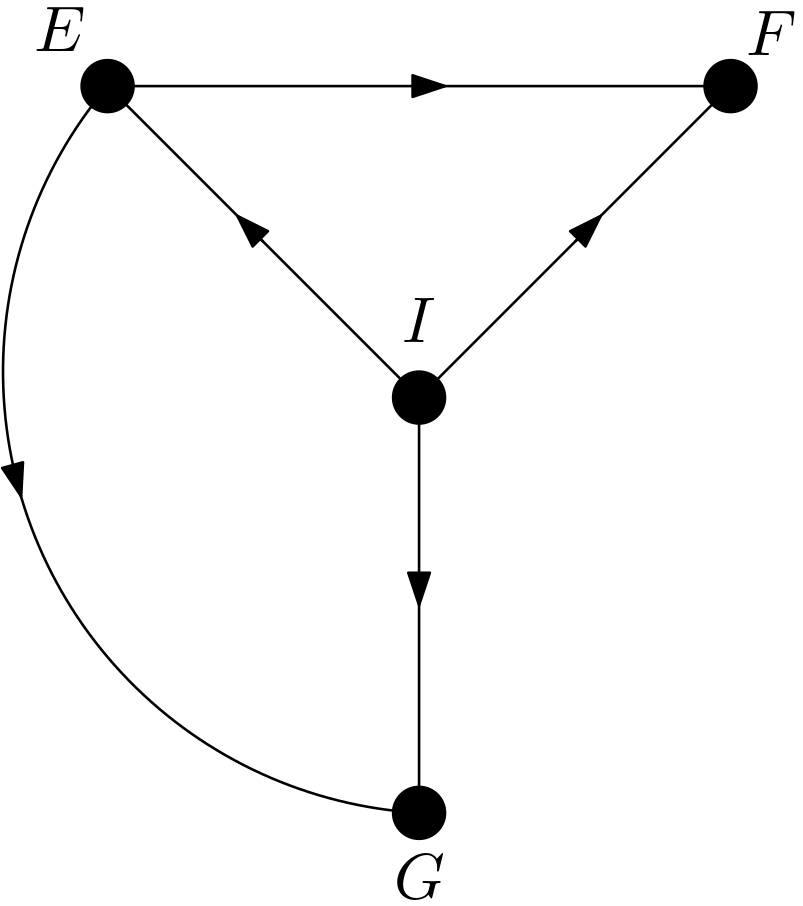
There are three paths from $G$ to $I$. They are listed as follows: \begin{equation} \begin{array}{l} 1) \, G \leftarrow E \leftarrow I \newline 2) \, G \leftarrow E \rightarrow F \leftarrow I \newline 3) \, G \leftarrow I \end{array} \end{equation} Only the second path is blocked due to the collider $E \rightarrow F \leftarrow I$. Hence, $I$ and $G$ cannot be d-separated in $G_{\underline{G}}$, which means that $p\left(i|do\left(g\right)\right)$ is not equal to $p\left(i|g\right)$.
Can the intervention on $G$ be removed or is $p\left(i|do\left(g\right)\right)$ equal to $p\left(i\right)$? For this removal or the equality to be valid, $I$ and $G$ must be d-separated in the DAG $G_{\overline{G}}$. $G_{\overline{G}}$ is shown in the Figure 7.
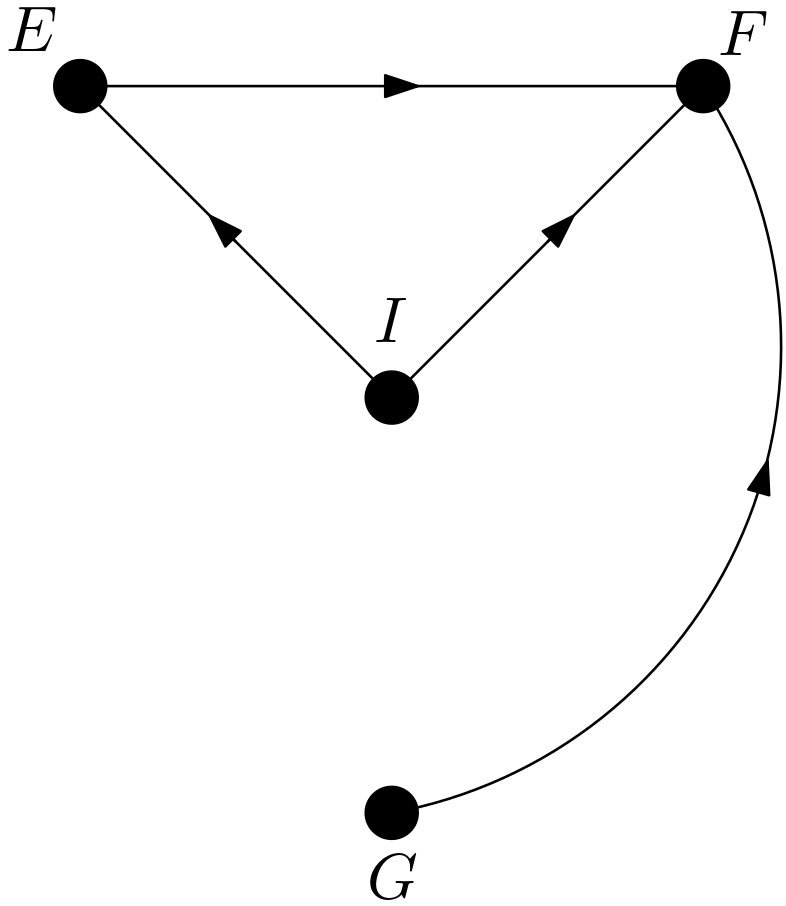
There are two paths from $G$ to $I$ in $G_{\overline{G}}$. They are as follows: \begin{equation} \begin{array}{l} 1) \, G \rightarrow F \leftarrow I \newline 2) \, G \rightarrow F \leftarrow E \leftarrow I \end{array} \end{equation} The first path is blocked due to its collider structure. The second path is blocked due to the collider $G \rightarrow F \leftarrow E$. Hence, $I$ and $G$ are d-separated in the DAG $G_{\overline{G}}$, which means that $p\left(i|do\left(g\right)\right)$ is equal to $p\left(i|e\right)$. The fifth causal effect has been shown to satisfy the following equality: \begin{equation} p\left(i|do\left(g\right)\right)=p\left(i\right) \end{equation} The next causal effect to be studied is $p\left(g|do\left(i\right)\right)$. Can the intervention on $I$ be replaced with observing $I$ or is $p\left(g|do\left(i\right)\right)$ equal to $p\left(g|i\right)$? For this replacement or equality to be possible, $G$ and $I$ must be d-separated in the DAG $G_{\underline{I}}$. The DAG $G_{\underline{I}}$ is shown in the Figure 4. As can easily be seen in the Figure 4, $G$ and $I$ are d-separated in $G_{\underline{I}}$, which means that $p\left(g|do\left(i\right)\right)$ is equal to $p\left(g|i\right)$. The sixth causal effect has been shown to satisfy the following equality: \begin{equation} p\left(g|do\left(i\right)\right)=p\left(g|i\right) \end{equation} The next causal effect to be examined is $p\left(e|do\left(f\right)\right)$. Can the intervention on $F$ be replaced with observing $F$ or is $p\left(e|do\left(f\right)\right)$ equal to $p\left(e|f\right)$? This replacement or equality is achievable if $E$ and $F$ are d-separated in the DAG $G_{\underline{F}}$. $G_{\underline{F}}$ is the same as $G$ which is shown in the Figure 1. The path $E \rightarrow F$ is enough to ensure that $E$ and $F$ are not d-separated in $G_{\underline{F}}$. Hence, $p\left(e|do\left(f\right)\right)$ cannot be written as $p\left(e|f\right)$.
Can the intervention on $F$ be removed or is $p\left(e|do\left(f\right)\right)$ equal to $p\left(e\right)$? This removal or equality is valid if $E$ and $F$ are d-separated in the DAG $G_{\overline{F}}$. $G_{\overline{F}}$ is displayed in the Figure 5. It can be observed that $E$ and $F$ are d-separated in the DAG $G_{\overline{F}}$, which means that $p\left(e|do\left(f\right)\right)$ can be written as $p\left(e\right)$. The seventh causal effect has been shown to satisfy the following equality: \begin{equation} p\left(e|do\left(f\right)\right)=p\left(e\right) \end{equation} The next causal effect to be studied is $p\left(e|do\left(g\right)\right)$. Can the intervention on $G$ be replaced with observing $G$ or is $p\left(e|do\left(g\right)\right)$ equal to $p\left(e|g\right)$? The replacement or the equality is possible if $E$ and $G$ are d-separated in the DAG $G_{\underline{G}}$. $G_{\underline{G}}$ is given in the Figure 6. The path $E \rightarrow G$ is enough to ensure that $E$ and $G$ are not d-separated in $G_{\underline{G}}$. Hence, $p\left(e|do\left(g\right)\right)$ cannot be written as $p\left(e|g\right)$.
Can the intervention on $G$ be removed or is $p\left(e|do\left(g\right)\right)$ equal to $p\left(e\right)$? The removal or the equality is valid if $E$ and $G$ are d-separated in the DAG $G_{\overline{G}}$. $G_{\overline{G}}$ is in the Figure 7. There are two paths between $E$ and $G$. They are as follows: \begin{equation} \begin{array}{l} 1) \, G \rightarrow F \leftarrow E \newline 2) \, G \rightarrow F \leftarrow I \rightarrow E \end{array} \end{equation} The first path is blocked due to its collider structure. The second path is blocked due to the collider $G \rightarrow F \leftarrow I$. Therefore, $E$ and $G$ are d-separated in the DAG $G_{\overline{G}}$, which means that $p\left(e|do\left(g\right)\right)$ can be written as $p\left(e\right)$. The eighth causal effect has been shown to satisfy the following equality: \begin{equation} p\left(e|do\left(g\right)\right)=p\left(e\right) \end{equation} The next causal effect to be studied is $p\left(f|do\left(e\right)\right)$. Can the intervention on $E$ be replaced with observing $E$ or is $p\left(f|do\left(e\right)\right)$ equal to $p\left(f|e\right)$? For the replacement or the equality to be possible, $F$ and $E$ must be d-separated in the graph $G_{\underline{E}}$. $G_{\underline{E}}$ is shown in the Figure 2. All of the paths between $F$ and $E$ are unblocked in $G_{\underline{E}}$. Hence, $F$ and $E$ cannot be d-separated, which means that $p\left(f|do\left(e\right)\right)$ cannot be written as $p\left(f|e\right)$. The unblocked paths are as follows: \begin{equation} \begin{array}{l} 1) \, E \leftarrow I \rightarrow F \newline 2) \, E \leftarrow I \rightarrow G \rightarrow F \end{array} \end{equation} These paths can be blocked by conditioning on $I$. Conditioning on $I$ blocks the first path that has a fork structure. Conditioning on $I$ blocks the fork $E \leftarrow I \rightarrow G$ in the second path. Hence, conditioning on $I$ should be incorporated into the calculation of $p\left(f|do\left(e\right)\right)$. It can be done as follows: \begin{equation} p\left(f|do\left(e\right)\right)=\sum_{i} p\left(f, i|do\left(e\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(f|do\left(e\right)\right)=\sum_{i}\frac{p\left(f,i|do\left(e\right)\right)}{p\left(i|do\left(e\right)\right)}p\left(i|do\left(e\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(f|do\left(e\right)\right)=\sum_{i} p\left(f|i,do\left(e\right)\right)p\left(i|do\left(e\right)\right) \end{equation} Since conditioning on $I$ blocks the paths between $F$ and $E$ in the DAG $G_{\underline{E}}$, $p\left(f|i,do\left(e\right)\right)$ is equal to $p\left(f|i,e\right)$. $p\left(i|do\left(e\right)\right)$ is the first causal effect found to be equal to $p\left(i\right)$. Therefore, the expansion for $p\left(f|do\left(e\right)\right)$ and so the ninth causal effect has been shown to satisfy the following equality: \begin{equation} p\left(f|do\left(e\right)\right)=\sum_{i} p\left(f|i,e\right)p\left(i\right) \end{equation} The next causal effect to be examined is $p\left(f|do\left(g\right)\right)$. Can the intervention on $G$ be replaced with observing $G$ or is $p\left(f|do\left(g\right)\right)$ equal to $p\left(f|g\right)$? The replacement or the equality is possible if $F$ and $G$ are d-separated in the graph $G_{\underline{G}}$. According to the Figure 6, the paths between $F$ and $G$ are as follows: \begin{equation} \begin{array}{l} 1) \, G \leftarrow E \leftarrow I \rightarrow F \newline 2) \, G \leftarrow E \rightarrow F \newline 3) \, G \leftarrow I \rightarrow E \rightarrow F \newline 4) \, G \leftarrow I \rightarrow F \end{array} \end{equation} All of these paths are unblocked. Hence, $F$ and $G$ are d-connected in the graph $G_{\underline{G}}$, which means that $p\left(f|do\left(g\right)\right)$ cannot be written as $p\left(f|g\right)$. Can these paths be blocked by conditioning on some variables? The answer is yes. Conditioning on both of $E$ and $I$ blocks these paths. Hence, conditioning on both of $E$ and $I$ should be incorporated into the calculation of the causal effect $p\left(f|do\left(g\right)\right)$. This can be done as follows: \begin{equation} p\left(f|do\left(g\right)\right)=\sum_{e}\sum_{i} p\left(f, e, i|do\left(g\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(f|do\left(g\right)\right)=\sum_{e}\sum_{i} \frac{p\left(f, e, i|do\left(g\right)\right)}{p\left(e, i| do\left(g\right)\right)}p\left(e, i| do\left(g\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(f|do\left(g\right)\right)=\sum_{e}\sum_{i} p\left(f|e, i, do\left(g\right)\right)p\left(e, i| do\left(g\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(f|do\left(g\right)\right)=\sum_{e}\sum_{i} p\left(f|e, i, do\left(g\right)\right) \frac{p\left(e, i| do\left(g\right)\right)}{p\left(i| do\left(g\right)\right)}p\left(i| do\left(g\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(f|do\left(g\right)\right)=\sum_{e}\sum_{i} p\left(f|e, i, do\left(g\right)\right) p\left(e|i, do\left(g\right)\right) p\left(i| do\left(g\right)\right) \end{equation} $p\left(f|e, i, do\left(g\right)\right)$ is equal to $p\left(f|e, i, g\right)$ since conditioning on $E$ and $I$ d-separates $F$ and $E$ in the DAG $G_{\underline{G}}$. For the calculation of $p\left(e|i, do\left(g\right)\right)$, the calculation of the eighth causal effect, $p\left(e|do\left(g\right)\right)$, can be utilized. In this calculation, it was determined that the intervention on $G$ could be removed. Can it also be removed while conditioning on $I$? Yes if $E$ and $G$ are conditionally d-separated given $I$ in the DAG $G_{\overline{G\left(I\right)}}$. $G\left(I\right)$ represents $G$ variable which is not an ancestor of $I$ in the DAG $G$ shown in the Figure 1. $G$ is not an ancestor of $I$ in the DAG G. Then, $G\left(I\right)$ is $G$. $E$ and $G$ are conditionally d-separated given $I$ in the graph $G_{\overline{G}}$ in the Figure 7. This means that the intervention on $G$ can still be removed while conditioning on $I$. Therefore, $p\left(e|i, do\left(g\right)\right)$ is equal to $p\left(e|i\right)$. $p\left(i|do\left(g\right)\right)$ has been calculated as the fifth causal effect and has been shown to be equal to $p\left(i\right)$. Then, the expansion for $p\left(f|do\left(g\right)\right)$ and the tenth causal effect has been shown to be as follows: \begin{equation} p\left(f|do\left(g\right)\right)=\sum_{e}\sum_{i} p\left(f|e, i, g\right) p\left(e|i\right) p\left(i\right) \end{equation} The next causal effect to be studied is $p\left(g|do\left(e\right)\right)$. Can the intervention on $E$ be replaced with observing $E$ or is $p\left(g|do\left(e\right)\right)$ equal to $p\left(g|e\right)$? The replacement or the equality is possible if $G$ and $E$ are d-separated in the DAG $G_{\underline{E}}$. $G_{\underline{E}}$ is in the Figure 2. The paths between $G$ and $E$ can be listed as follows: \begin{equation} \begin{array}{l} 1) \, E \leftarrow I \rightarrow G \newline 2) \, E \leftarrow I \rightarrow F \leftarrow G \end{array} \end{equation} The first path is unblocked due to its fork structure. The second path is blocked due to the collider $I \rightarrow F \leftarrow G$. Therefore, due to the first path, $G$ and $E$ are d-connected in $G_{\underline{E}}$, which means that $p\left(g|do\left(e\right)\right)$ cannot be written as $p\left(g|e\right)$. But, the first path can be blocked by conditioning on $I$. So, conditioning on $I$ should be included in the solution. The inclusion can be made as follows: \begin{equation} p\left(g|do\left(e\right)\right)=\sum_{i} p\left(g,i|do\left(e\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(g|do\left(e\right)\right)=\sum_{i} \frac{p\left(g,i|do\left(e\right)\right)}{p\left(i|do\left(e\right)\right)}p\left(i|do\left(e\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(g|do\left(e\right)\right)=\sum_{i} p\left(g|i,do\left(e\right)\right)p\left(i|do\left(e\right)\right) \end{equation} $p\left(g|i,do\left(e\right)\right)$ is equal to $p\left(g|i,e\right)$ since conditioning on $I$ d-separates $G$ and $E$ in the graph $G_{\underline{E}}$. $p\left(i|do\left(e\right)\right)$ has been calculated as the first causal effect and is equal to $p\left(i\right)$. So, the expansion for $p\left(g|do\left(e\right)\right)$ and the eleventh causal effect can be written as follows: \begin{equation} p\left(g|do\left(e\right)\right)=\sum_{i} p\left(g|i,e\right)p\left(i\right) \end{equation} The next causal effect to be examined is $p\left(g|do\left(f\right)\right)$. Can the intervention on $F$ be replaced with observing $F$ or is $p\left(g|do\left(f\right)\right)$ equal to $p\left(g|f\right)$? For the replacement or the equality to be possible, $G$ and $F$ must be d-separated in the DAG $G_{\underline{F}}$. $G_{\underline{F}}$ is the same as $G$ in the Figure 1. Due to the path $G \rightarrow F$, the d-separation of $G$ and $F$ is impossible, which means that $p\left(g|do\left(f\right)\right)$ cannot be written as $p\left(g|f\right)$.
Can the intervention on $F$ be removed or is $p\left(g|do\left(f\right)\right)$ equal to $p\left(g\right)$? The removal or the equality is possible if $G$ and $F$ are d-separated in the graph $G_{\overline{F}}$. In the Figure 5, it is easily seen that $G$ and $F$ are d-separated in $G_{\overline{F}}$. Hence, the removal is possible. The twelfth causal effect has been shown to satisfy the following equality: \begin{equation} p\left(g|do\left(f\right)\right)=p\left(g\right) \end{equation} The DAG in the Figure 1 has been shown to be identifying all of the basic twelve causal effects in the form of $p\left(y|do\left(x\right)\right)$. This is an expected result due to the theorem 3.6.1 on the page 105 of [4]. The theorem states a sufficient condition for a graph to be identifying a causal effect in the form of $p\left(y|do\left(x\right)\right)$. It is quoted as follows:
A sufficient condition for identifying the causal effect $p\left(y|do\left(x\right)\right)$ is that there exists no bi-directed path (i.e., a path composed entirely of bi-directed arcs) between $X$ and any of its children. [5]
Since there are no bidirected arcs in the DAG in the Figure 1, the causal effects in the form of $p\left(y|do\left(x\right)\right)$ must be identified by the DAG according to the theorem.
Conclusion
The basic causal effects in the form of $p\left(y|do\left(x\right)\right)$ have been calculated for the DAG in the Figure 1.
References
[4] Judea Pearl, Causality: Models, Reasoning and Inference, Cambridge University Press, 2009.
[5] J. Tian and J. Pearl. A general identification condition for causal effects. In Proceedings of the Eighteenth National Conference on Artificial Intelligence, pages 567–573. AAAI Press/ The MIT Press, Menlo Park, CA, 2002.