Introduction
In the article [1], directed acyclic graphs (DAGs) from an equivalence class for an image were given. These DAGs contained four features and these features were assumed to be dependent on each other. In this article, the case when there are five features is to be examined. An immediate simple generalization for the case of $n$ features is to be made. The upper limit for the number of features for generating DAGs from an equivalence class will be questioned. There will be some discussion about the autonomies of the mechanisms represented by arrows in the DAGs.
Five Feature Case and The General Case
The features are called $E$, $F$, $G$, $H$ and $I$. For the time being, there is no information about what these features are. The only information is that these features represent sets of pixels of the image studied. These features are assumed to contain relatively large numbers of pixels compared to the total number of pixels in the image so that they are dependent on each other. In the Figure 1,
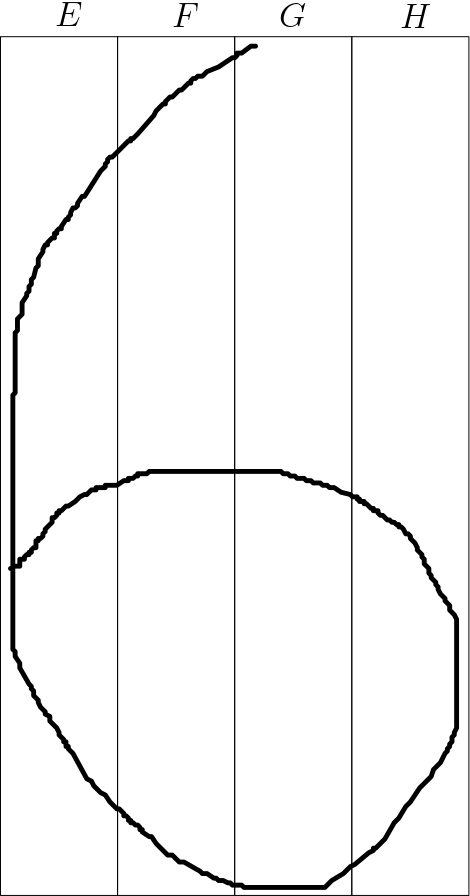
the four features are shown to be the representations of the pixels bounded by the four triangles. $I$ is the intent with wihich the image is created. It can be considered as the label of the image. Due to their relatively large numbers of pixels compared to the total number of pixels in the image, the feaures are dependent on each other. $I$ is one of the causes of the features $E$, $F$, $G$ and $H$. To guarantee that the features are dependent on each other, each feature is made to be connected to other features by arrows. One of the DAGs satisfying the condition that each feature is connected to the other features and $I$ is the effect of the other features is shown in the Figure 2.
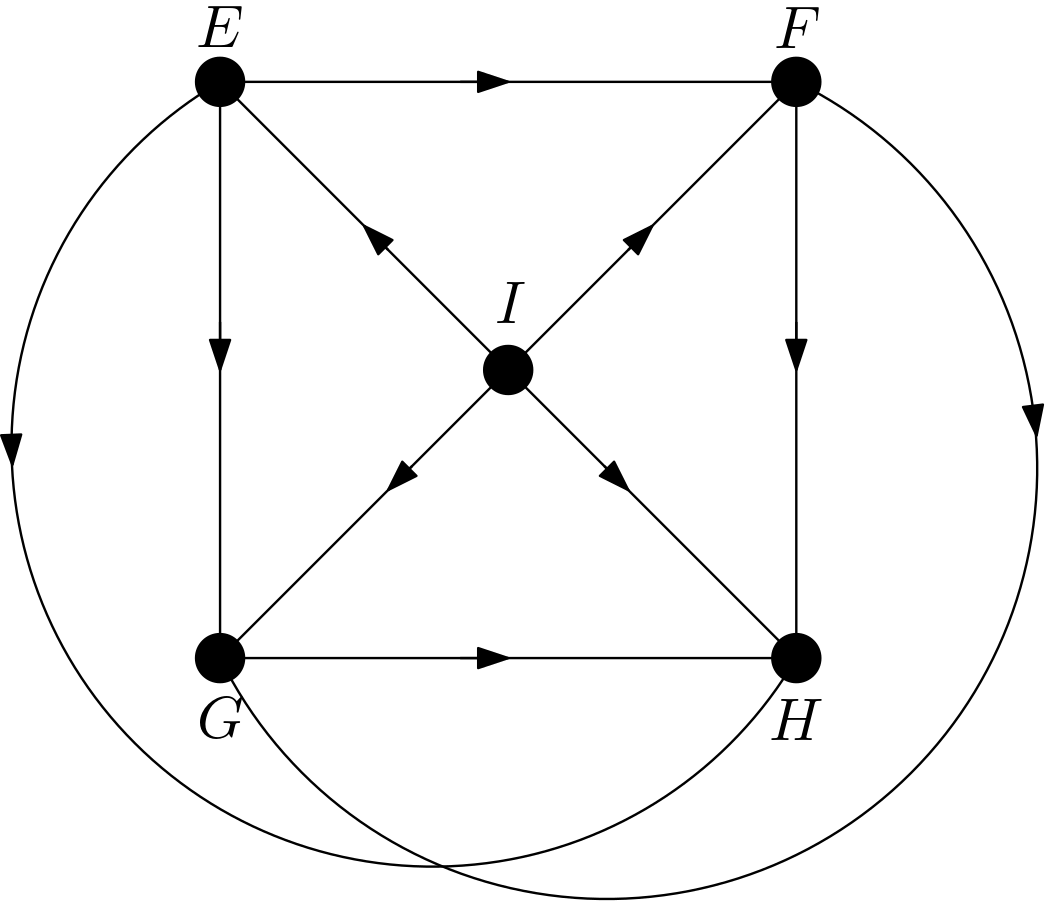
The other DAGs can be obtained by changing the node names of the vertices of the square $EFGH$. Hence, there are $4!=24$ DAGs. All these 24 DAGs are shown in the Figure 3.

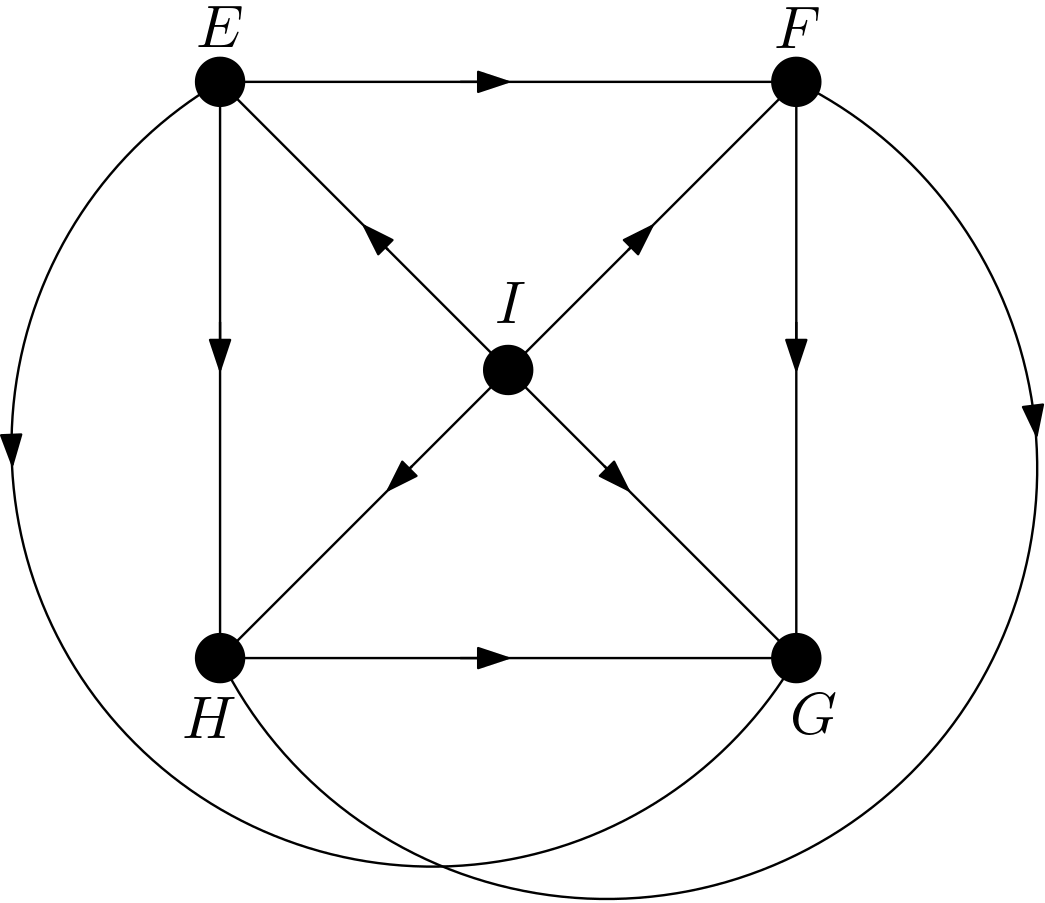
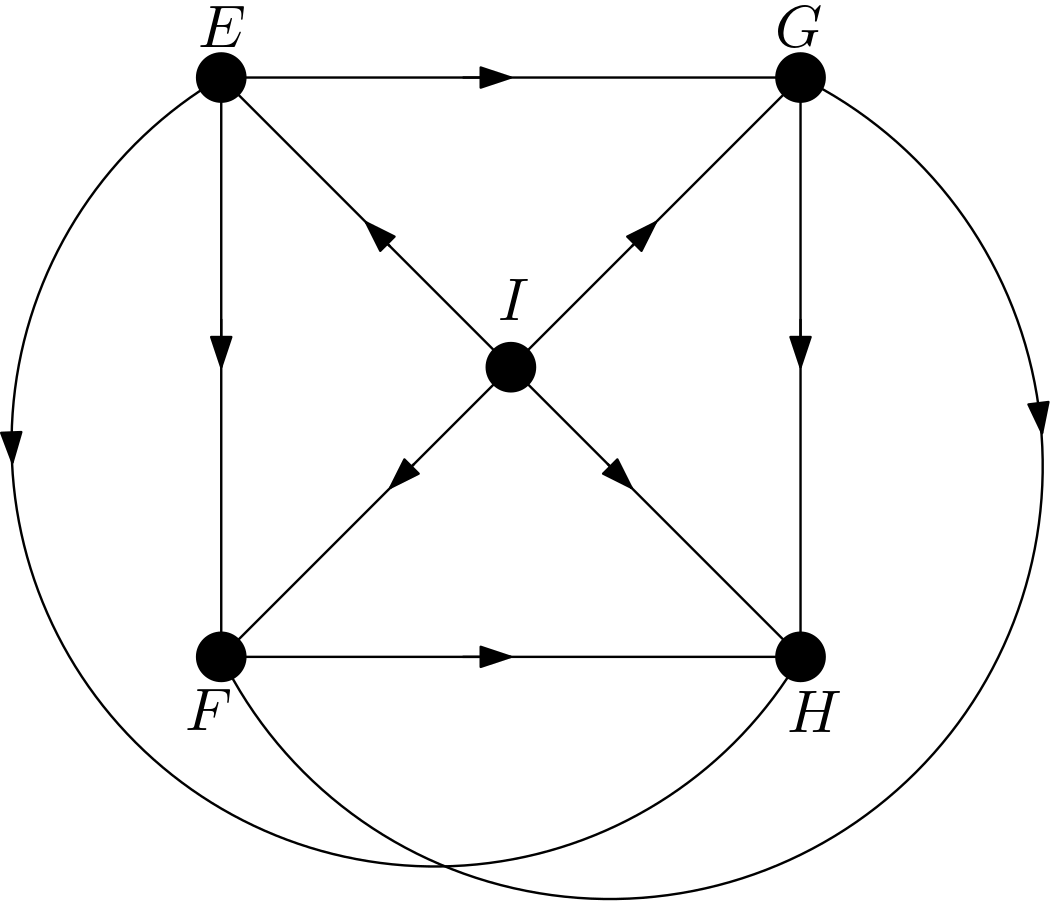
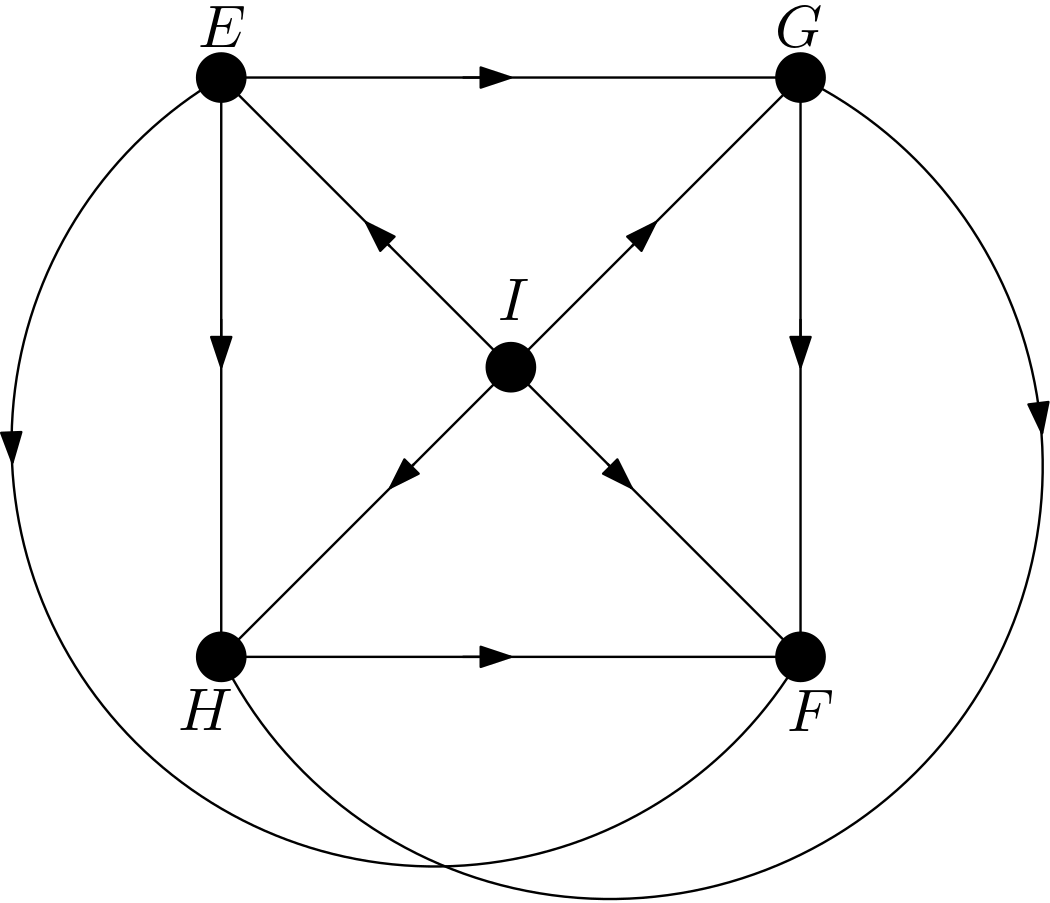
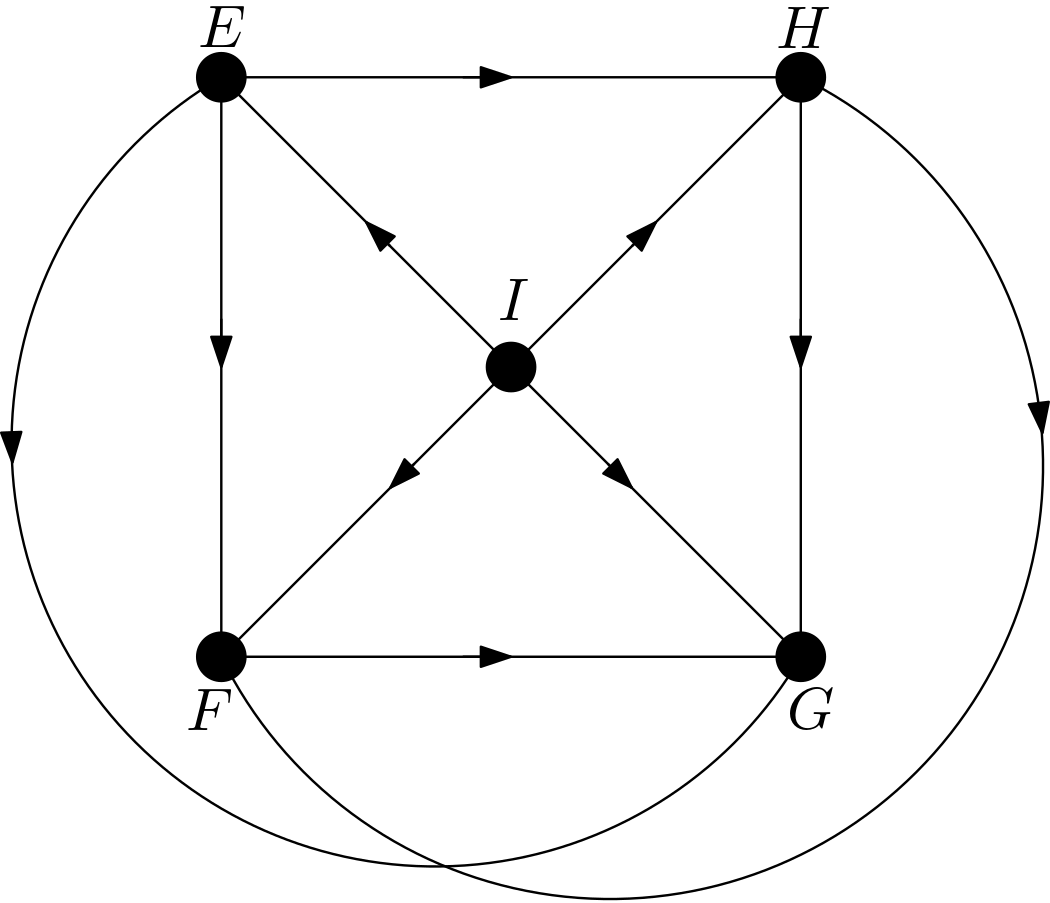
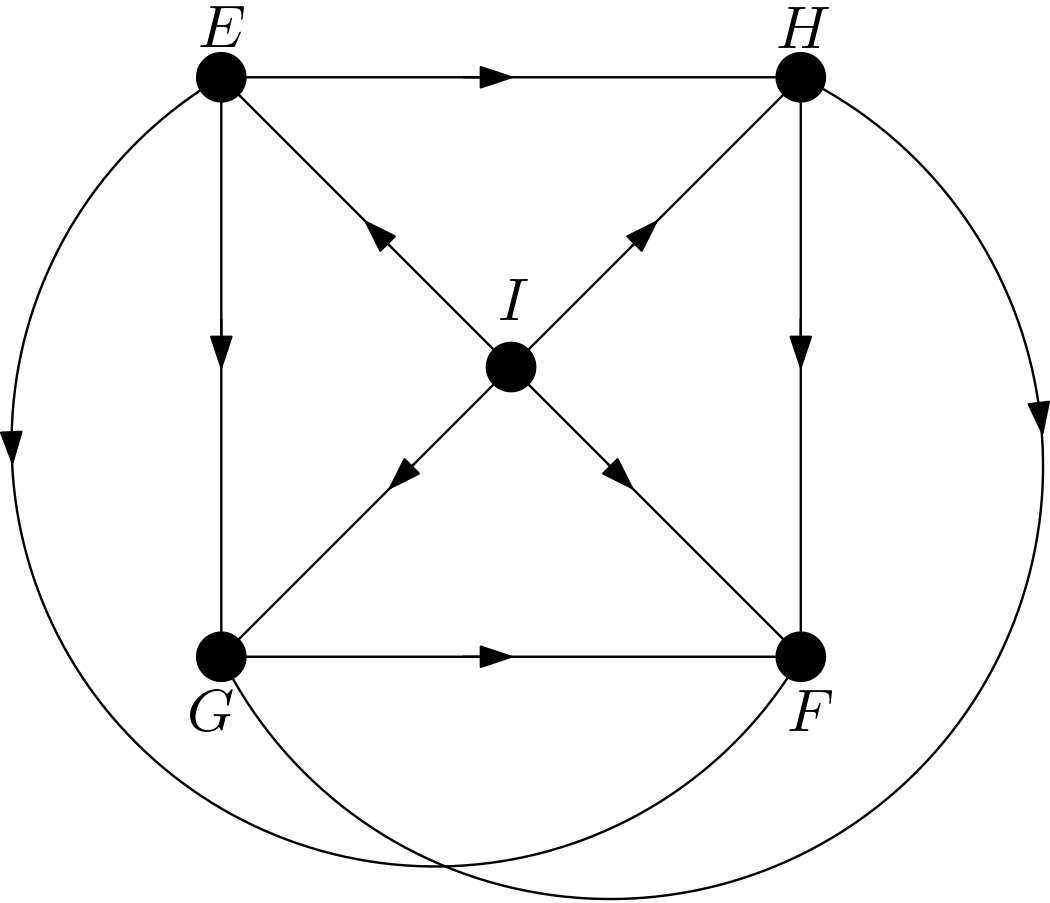
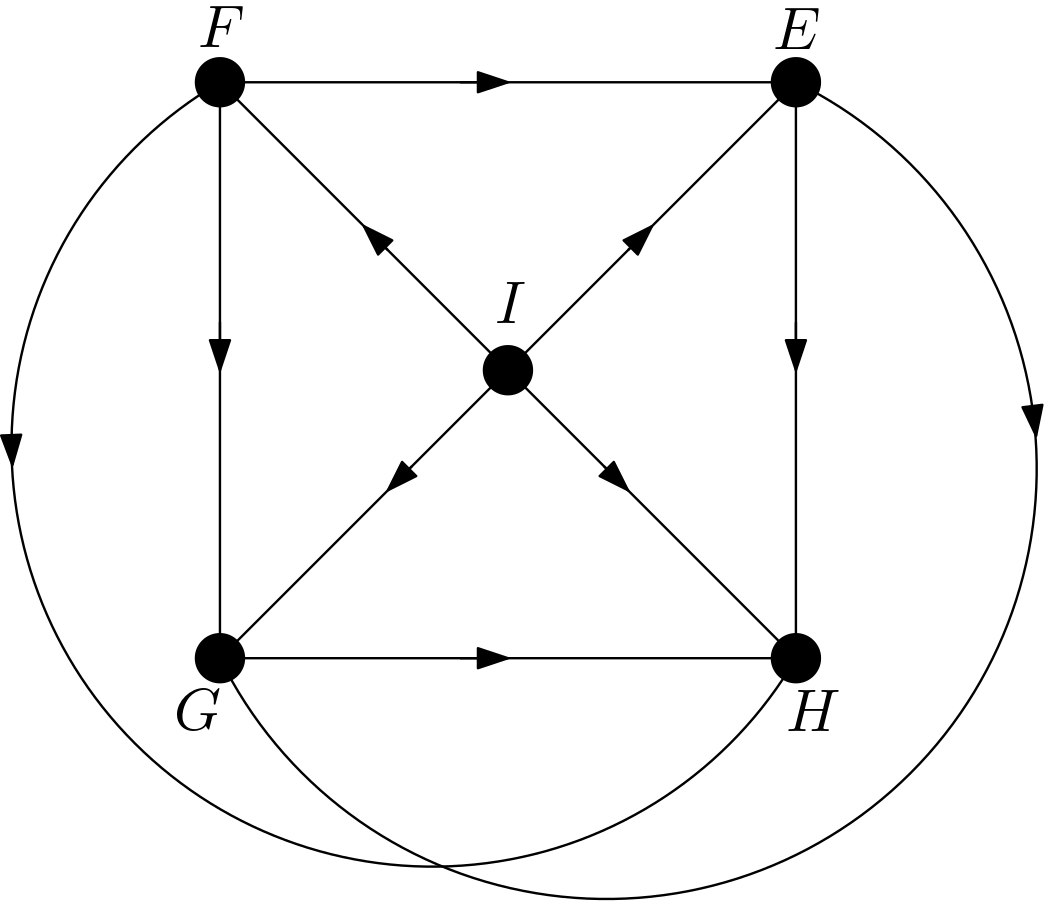
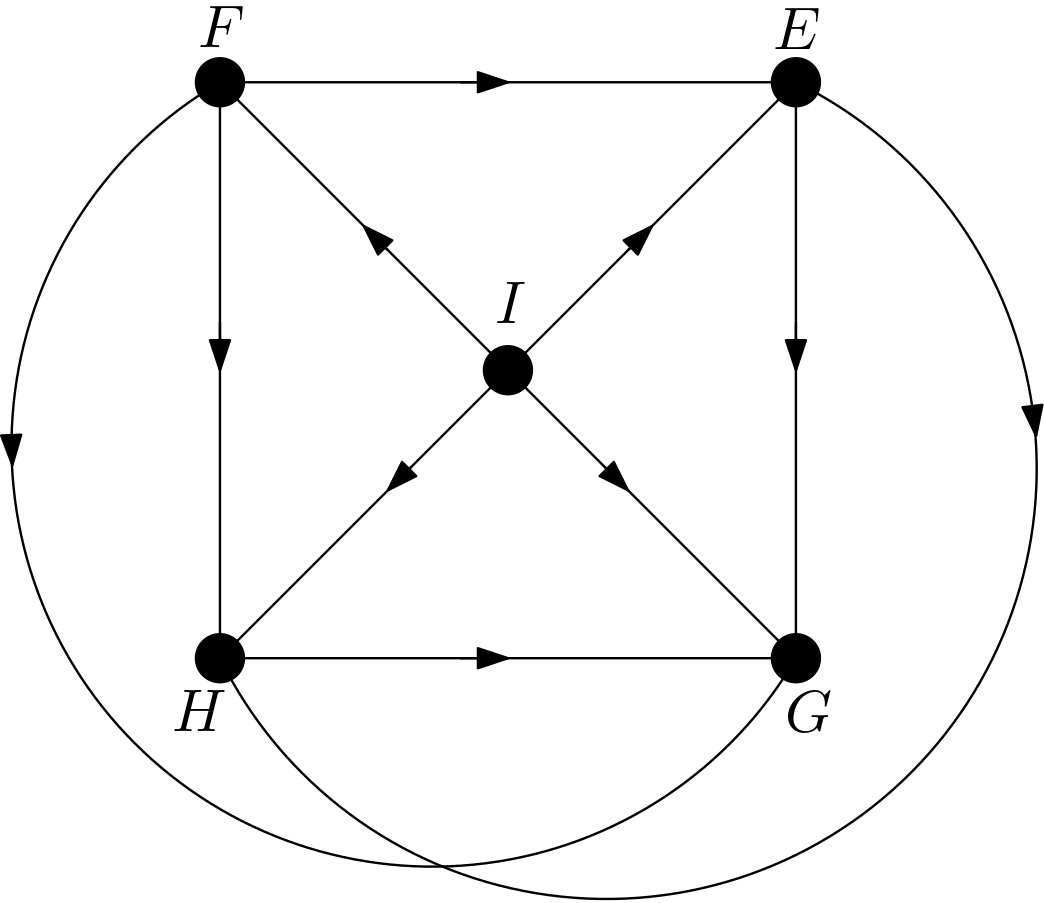
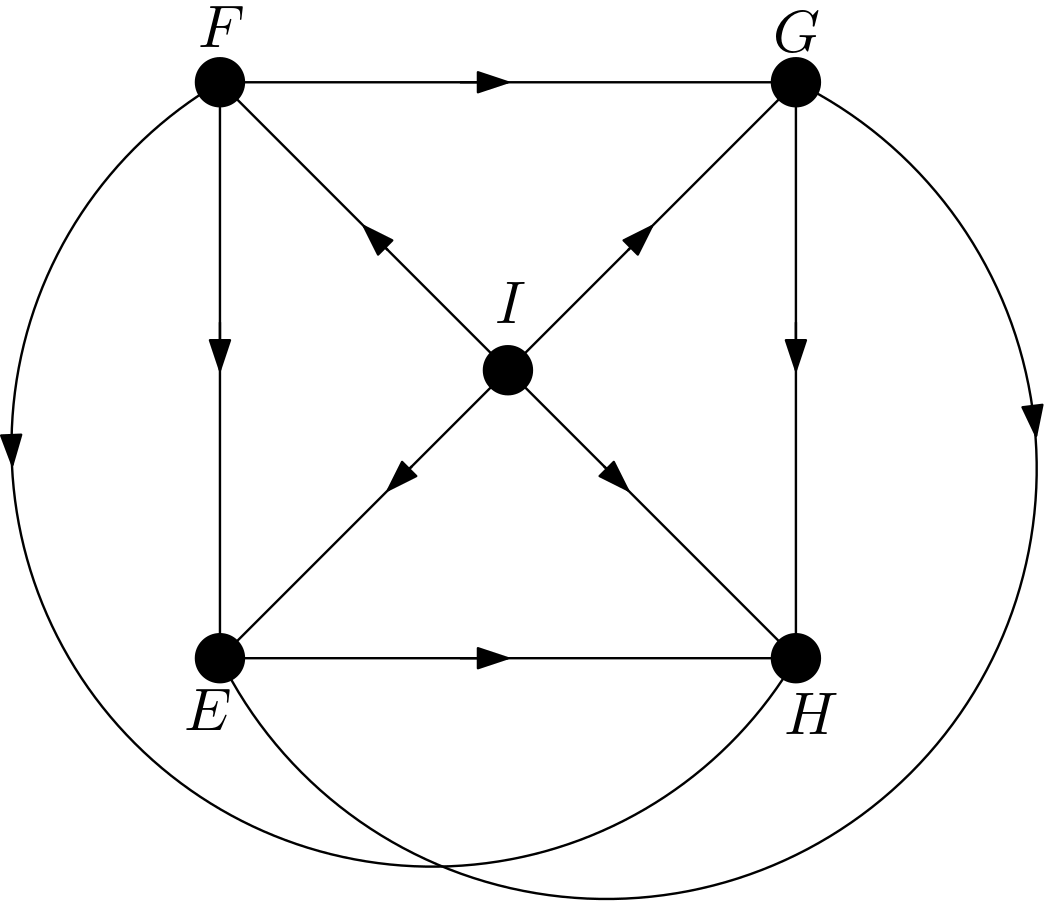
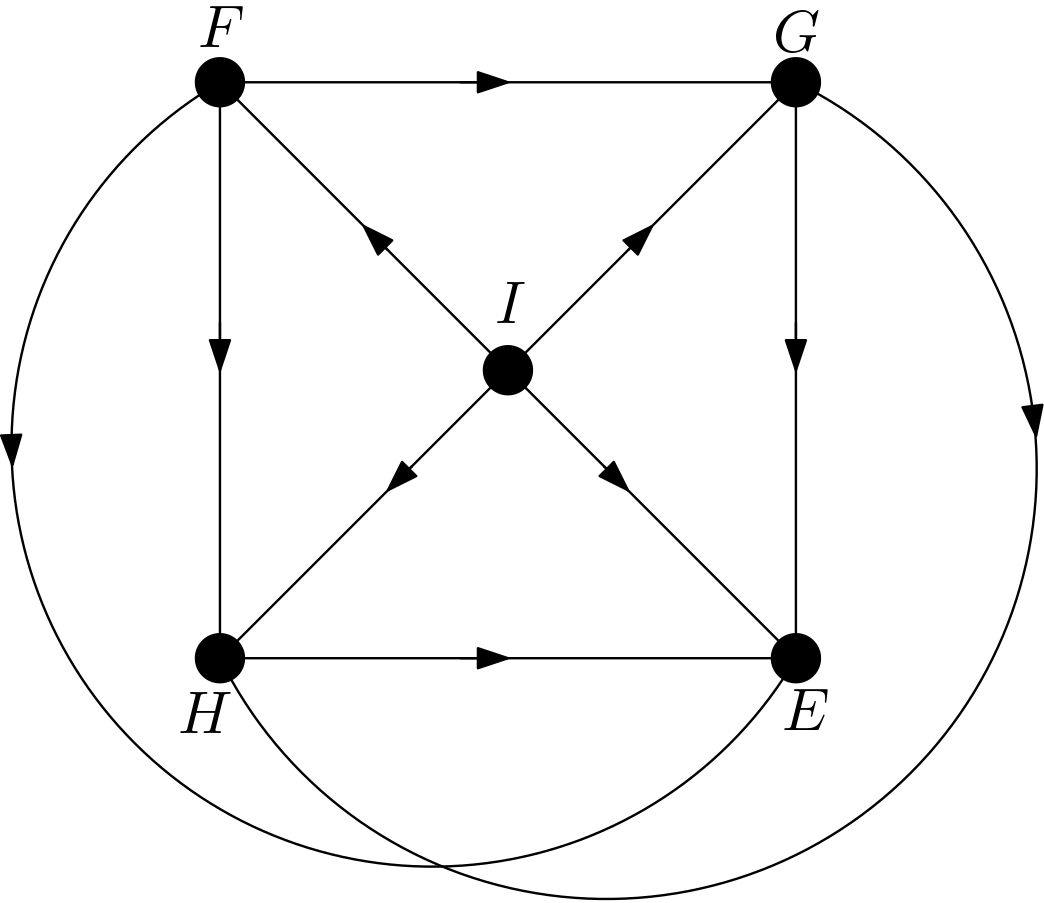
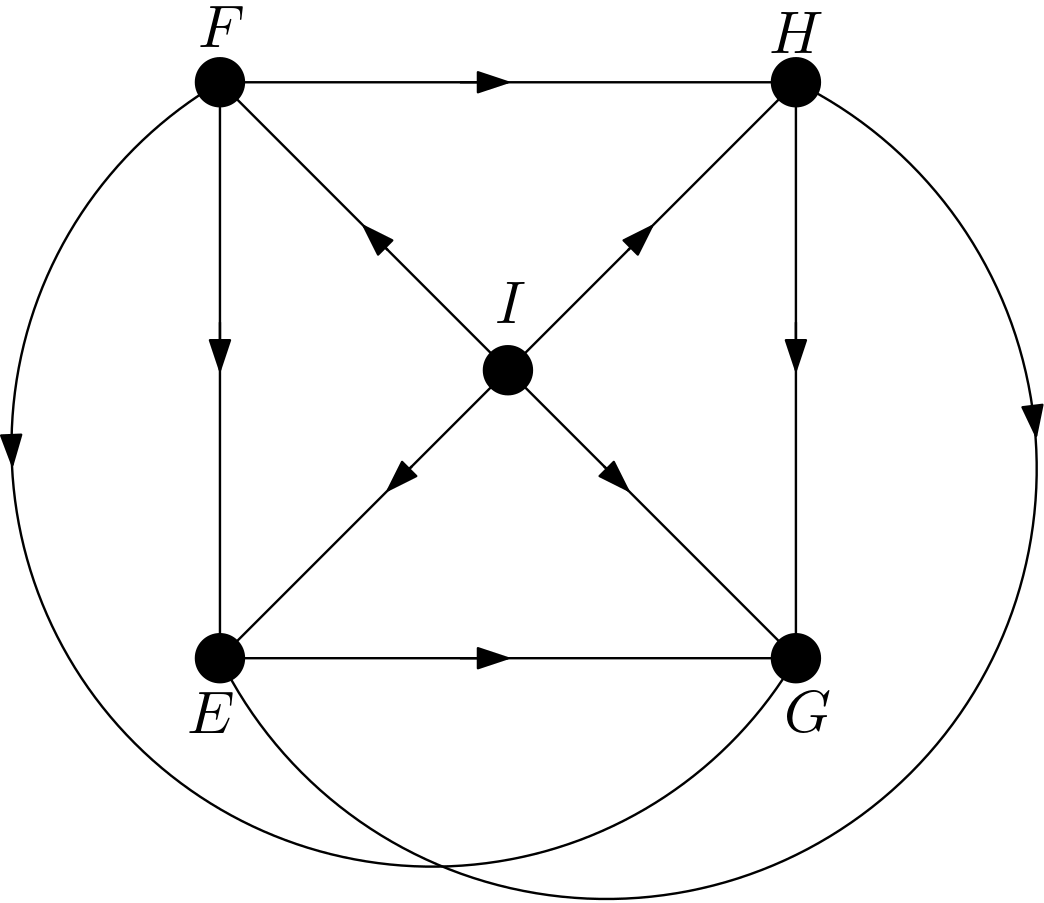
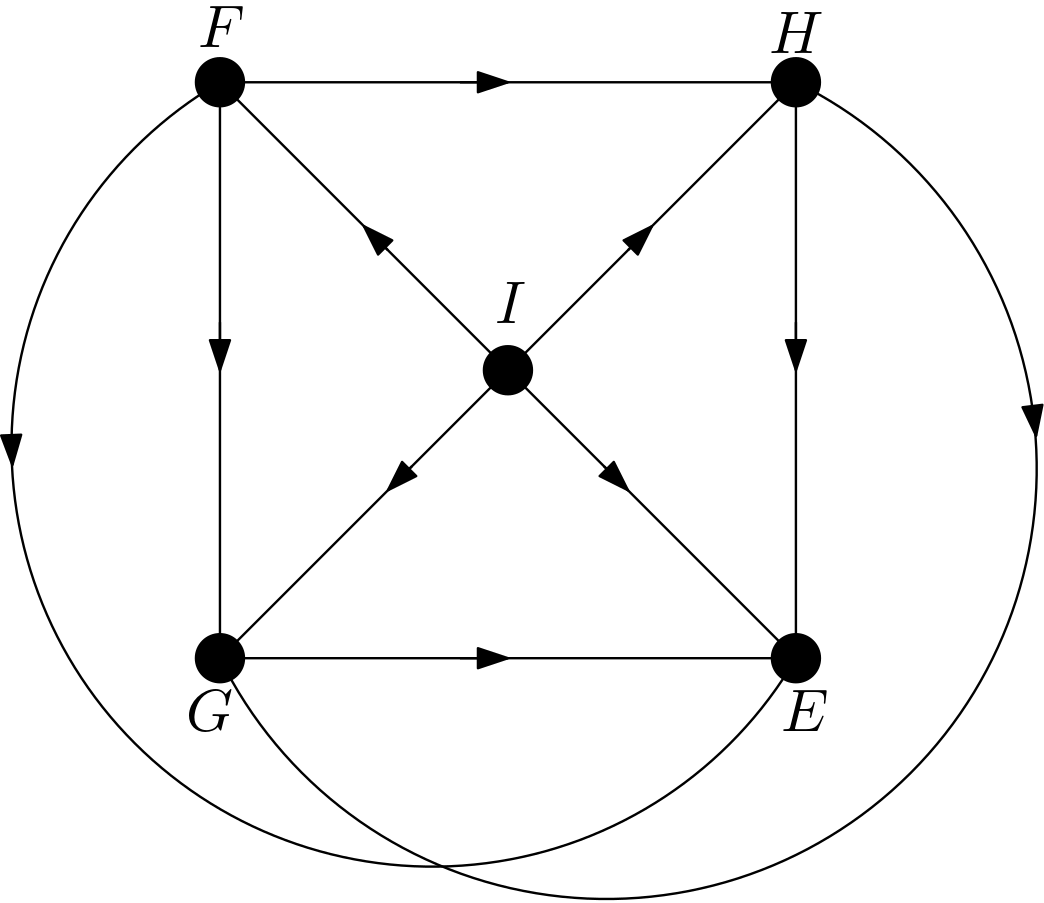
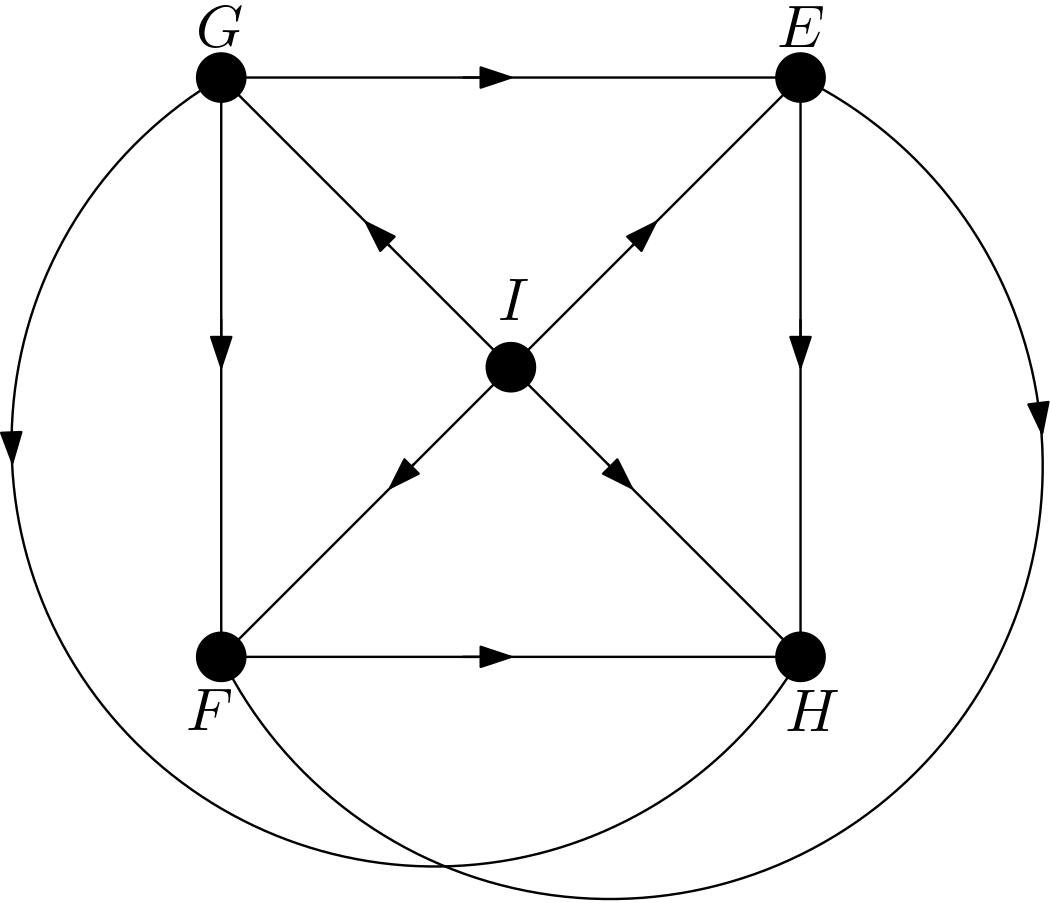
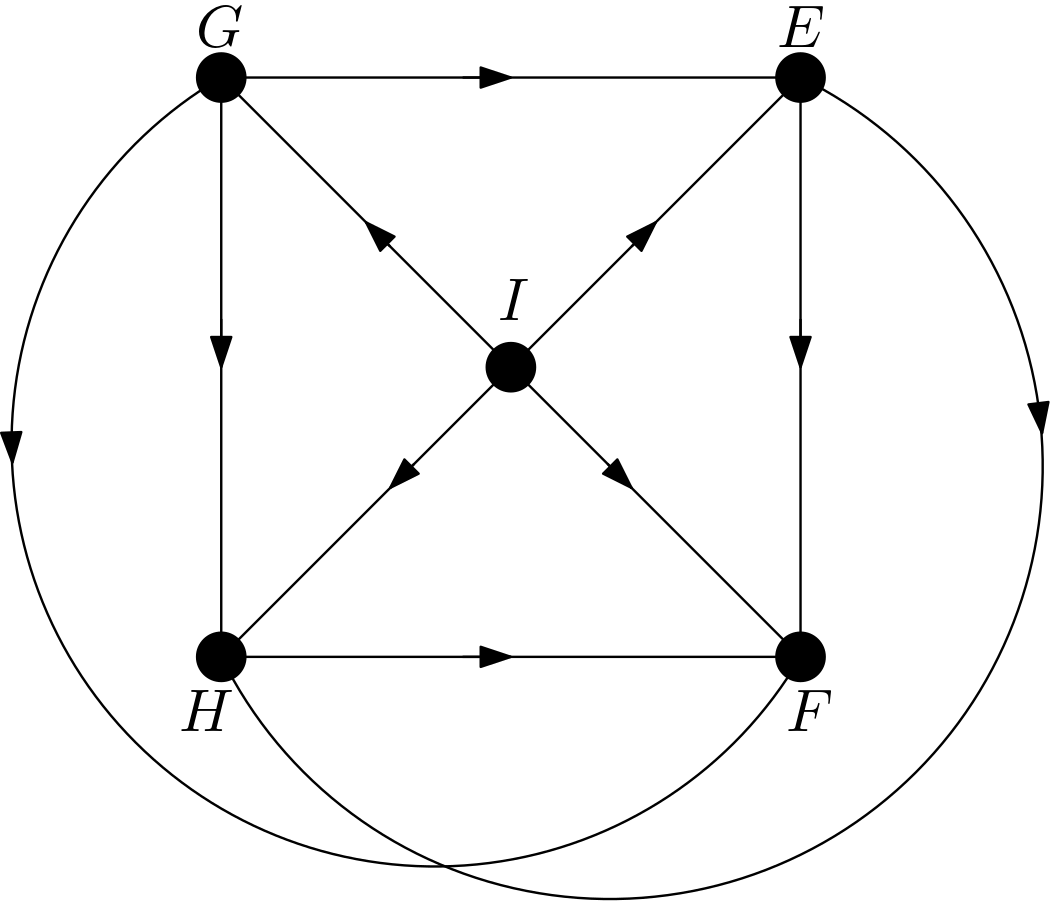
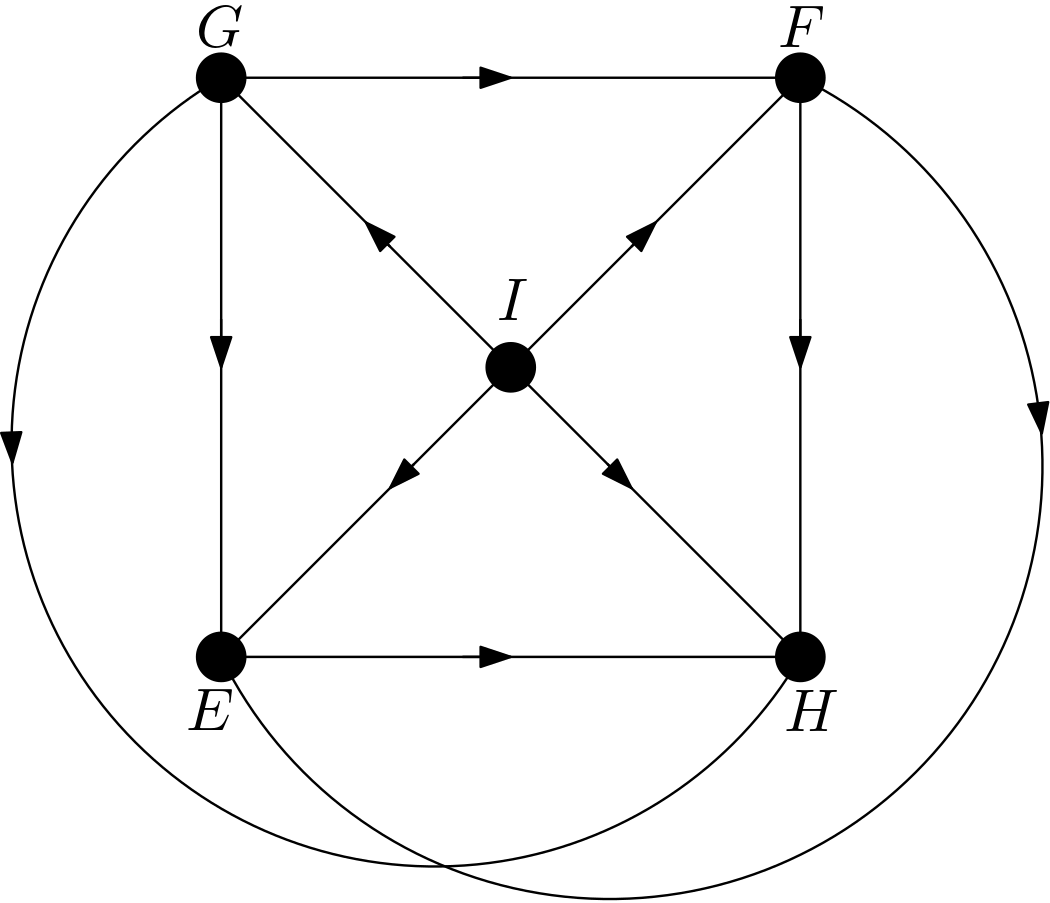
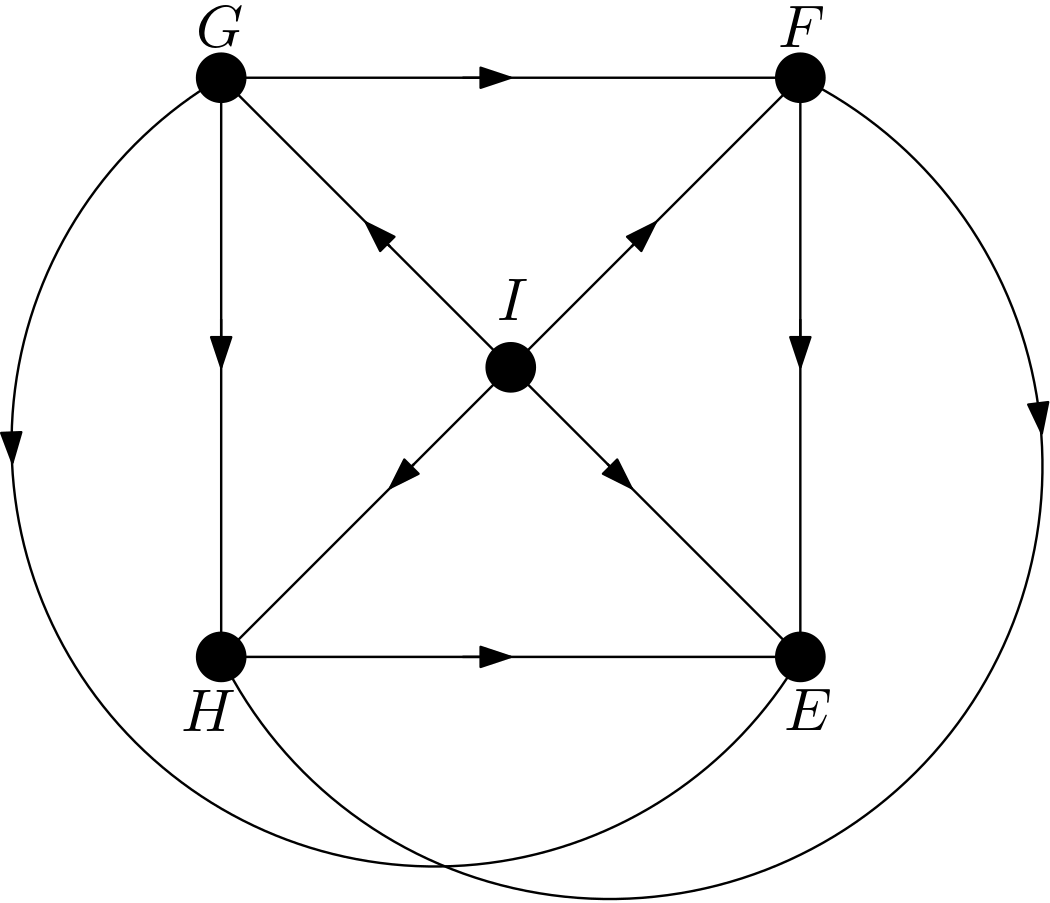
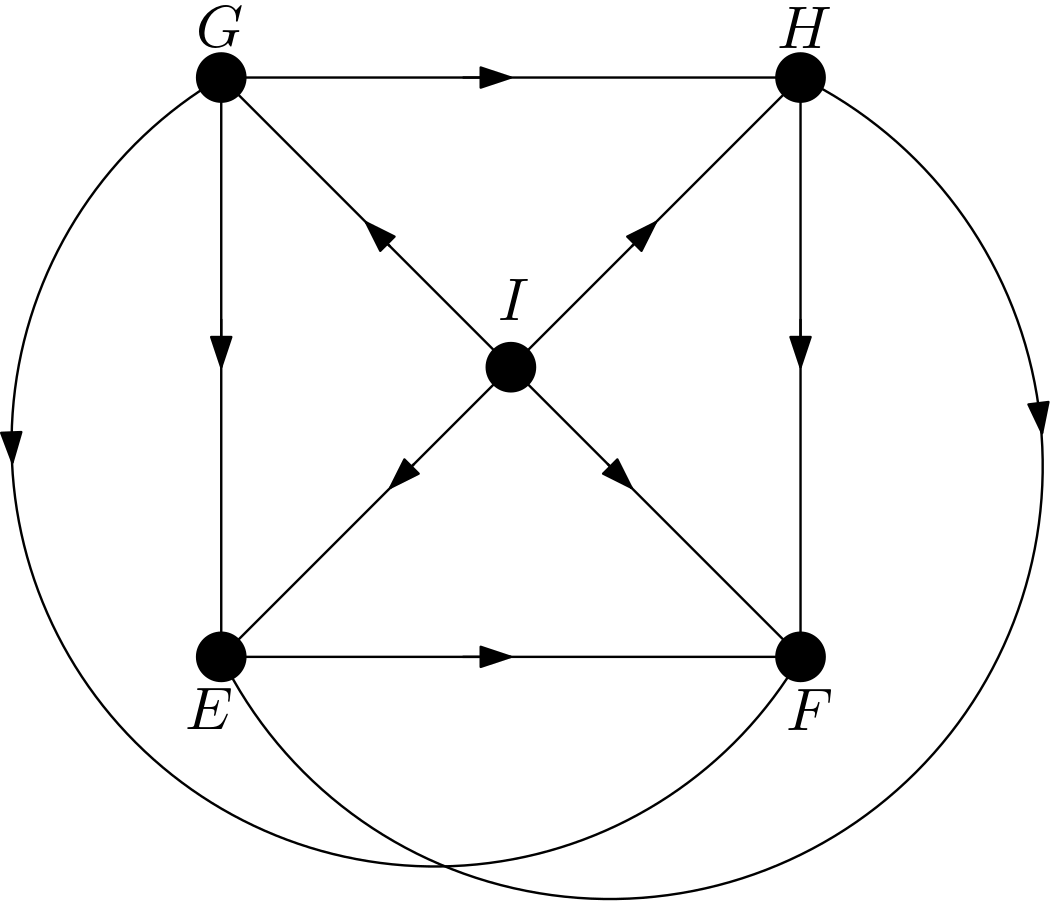
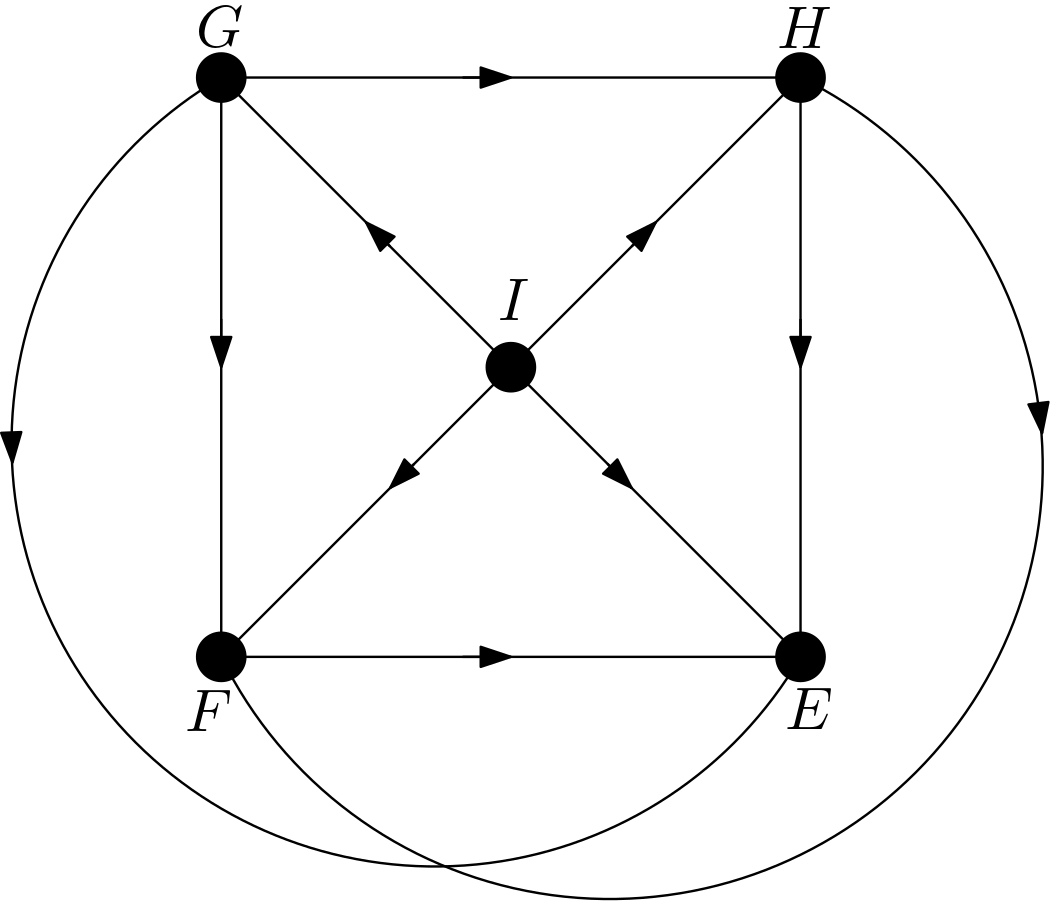
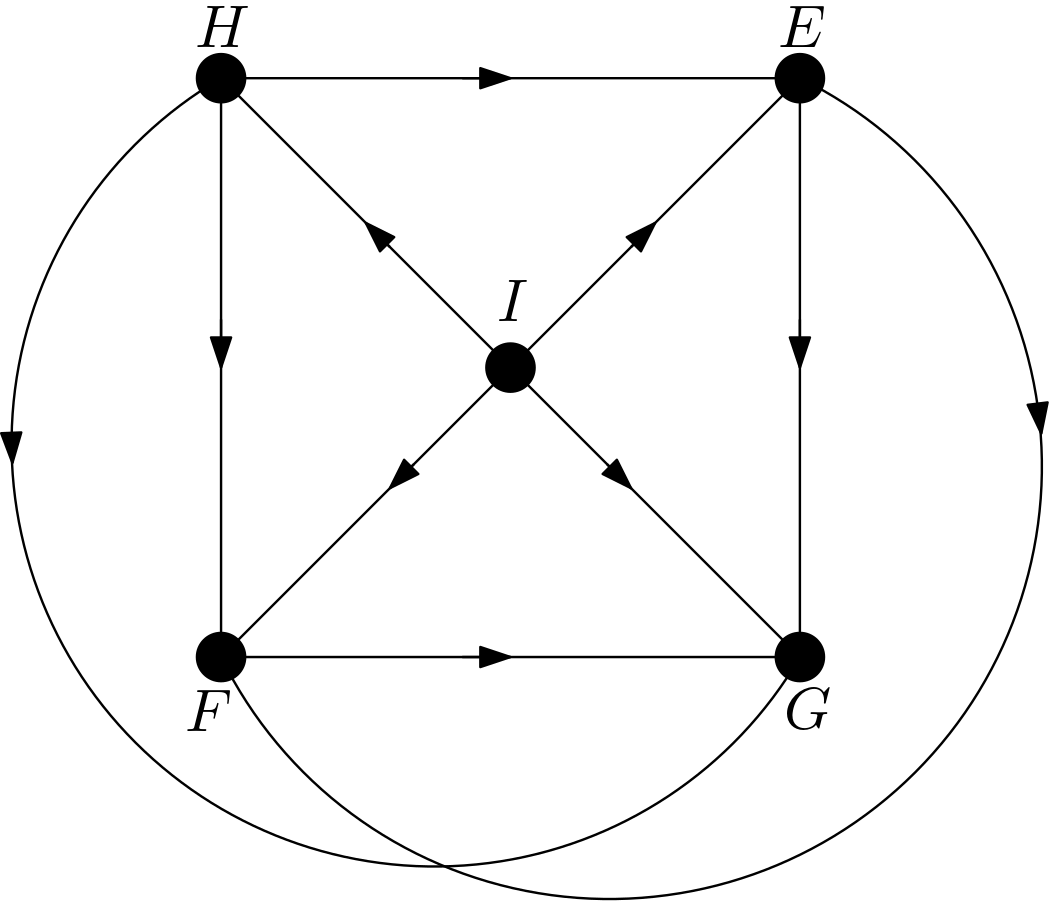
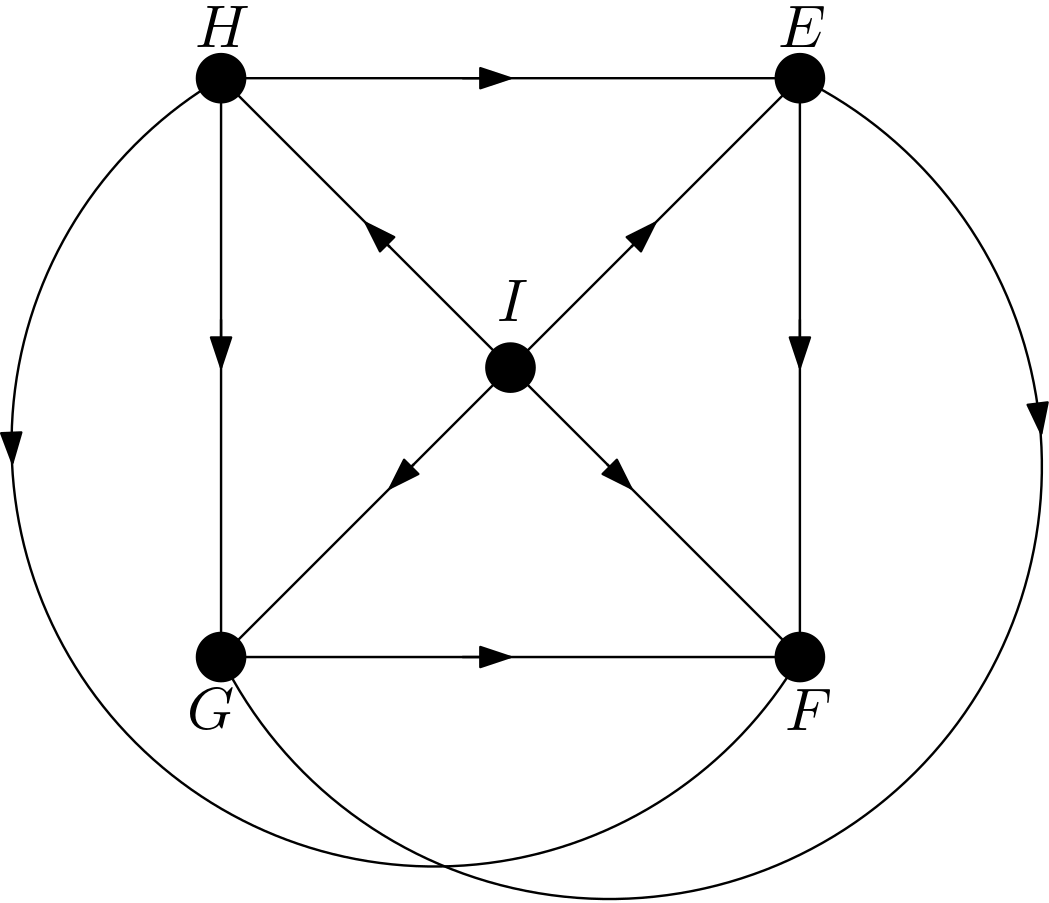
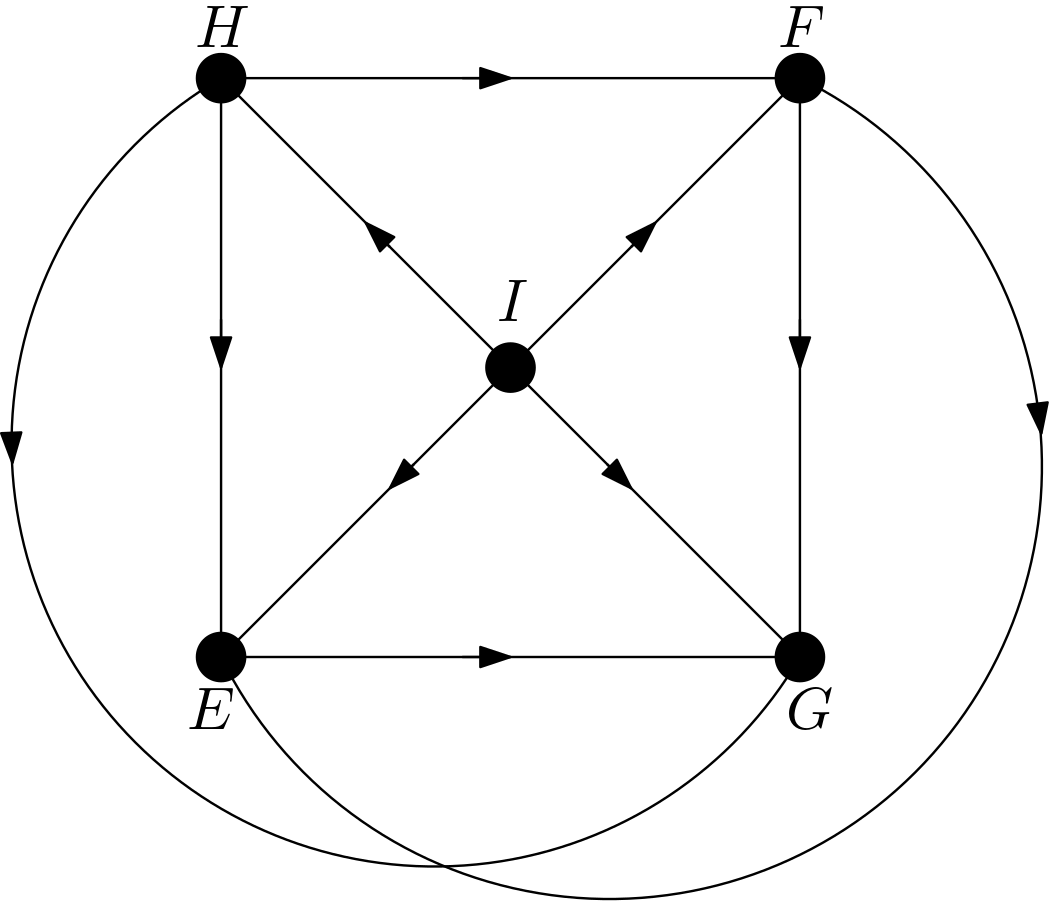
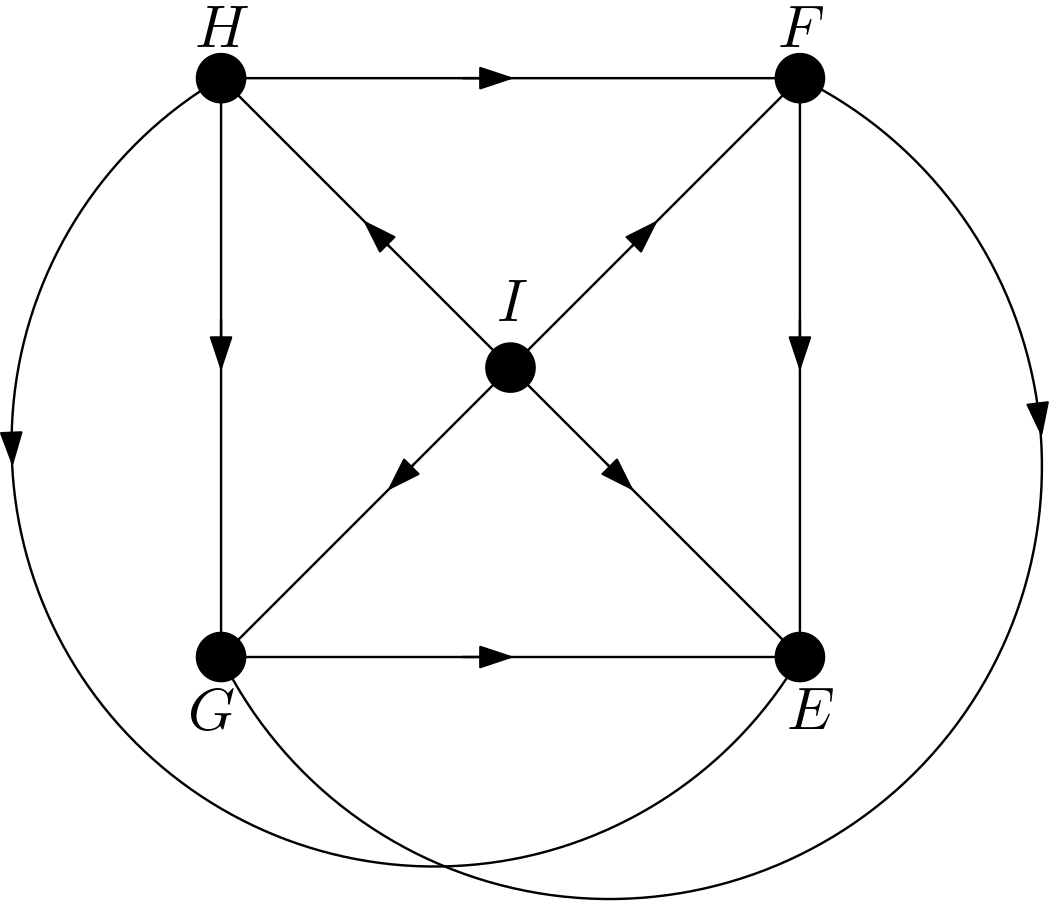
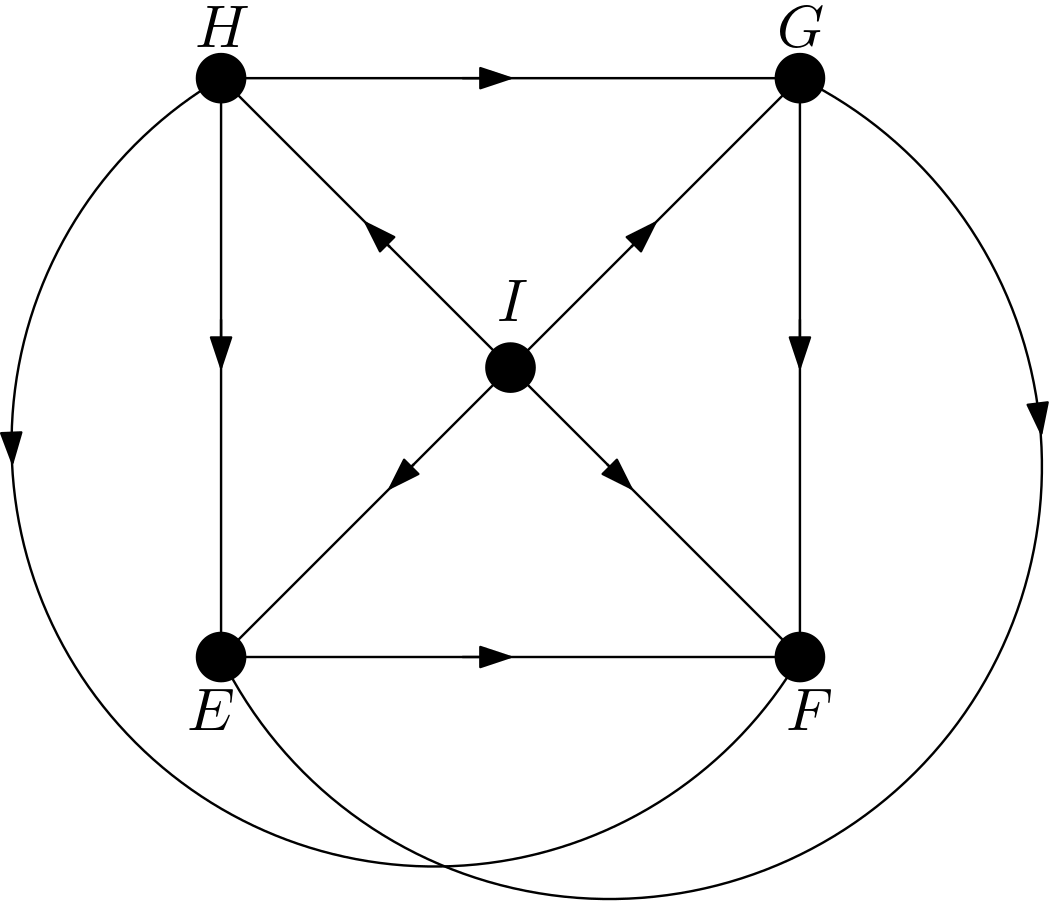
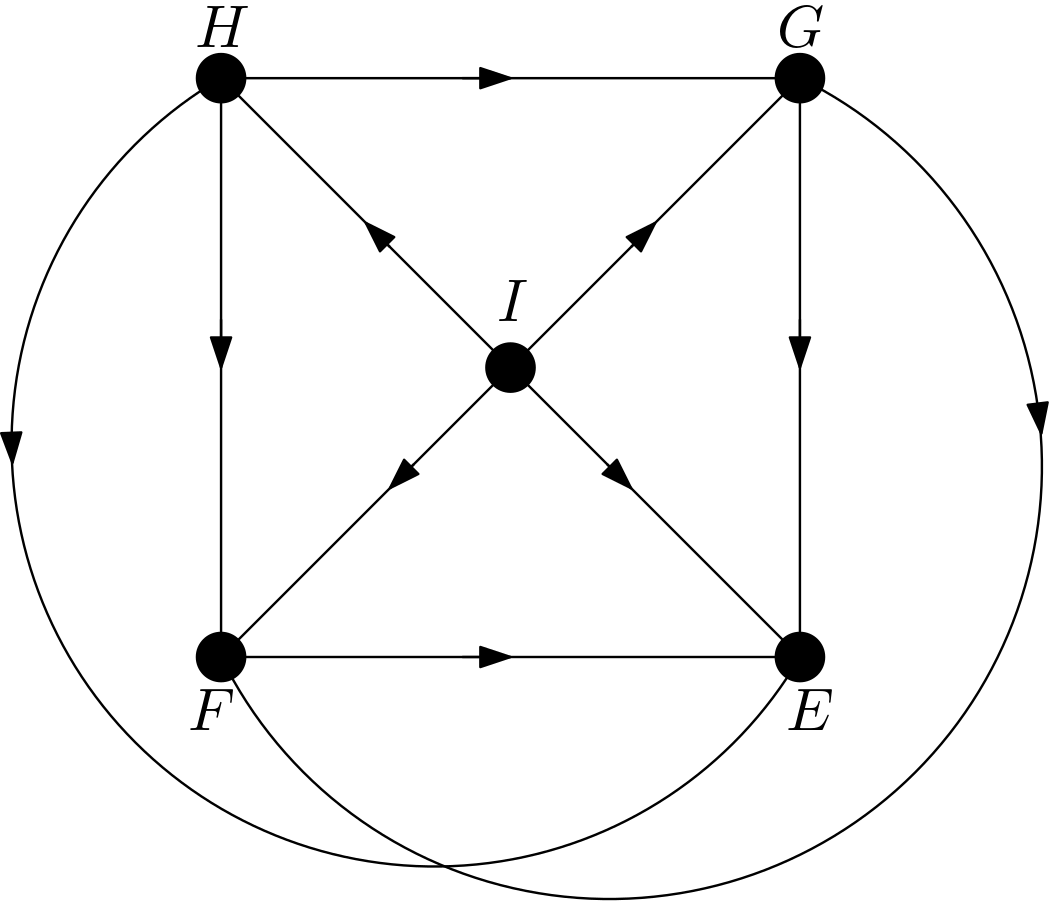
Using the DAGitty package [2] from R, it has been verified that the first DAG in the Figure 3 has no d-separation implication. The other 23 DAGs in the Figure 3 are obtained only by changing the names of the vertices of the square. Hence, there must not be any d-separation implications for them, either. This is in accordance with the expectation that all the features should be dependent on each other due to the their large number of pixels compared to the total number of pixels in the image. There can be no v-structures in the 24 DAGs since each feature is connected to the other features. All 24 DAGs share the same skeleton. Hence, these 24 DAGs are from the same equivalence class.
An immediate and simple generalization can be made for the case of $n$ features. There will be a total of $n!$ DAGs from the same equivalence class for an image. However, as the number of features increases, the assumption that all of the features are dependent on each other will gradually become wrong. Therefore, the number of features in the DAG must have an upper limit. The assumption that all of the features are dependent on each other should be tested using the available set of images. Using this test, the upper limit can be determined.
A Discussion About The Autonomies Of The Mechanisms In The DAGs
Let the definition of autonomy be quoted from the page 63 of [3] as follows:
…rests on the notion of autonomy (Aldrich 1989), a notion at the heart of all causal concepts (see Sections 1.3 and 1.4). A causal model is not just another scheme of encoding probability distribution through a set of parameters. The distinctive feature of causal models is that each variable is determined by a set of other variables through a relationship (called mechanism) that remans invariant when other mechanisms are subjected to external influences. This invariance means that mechanisms can vary independently of one another, which in turns implies that the set of structural coefficients (e.g., $\alpha$, $\beta$, $\gamma$ in our example of (2.2))- rather than other types of parameters (e.g., $\rho_{YZ}$, $\rho_{XZ}$, $\rho_{YX}$)- can and will vary independently when experimental conditions change. Consequently, equality constraints of the form $\alpha=-\beta\gamma$ are contrary to the idea of autonomy and will rarely occur under natural conditions…
According to this explanation of autonomy, some discussion about the mechanisms represented by the arrows in the DAGs from the same equivalence class of an image is to be made. This discussion is about the question if they satisfy the autonomy condition. The part of the digit six denoted by the feature $E$ should be drawn in a way similar to the one as shown in the Figure 1. This way of drawing the part represented by the feature $E$ is independent of the way the other parts of the image are drawn. Whatever intervention is made to the other parts of the digit, the part represented by the feature $E$ should be drawn in a way similar to the one shown in the Figure 1. According to this way of thinking, the mechanisms seem to be autonomous. The features and the mechanisms should mathematically be defined in compliance with this way of thinking so that the mechanisms become autonomous.
Conclusion
The DAGs from the equivalence class of an image for the case of five features have been generated. The number of DAGs for the general case of $n$ features has been given. It has been stated how the upper limit for the number of features can be found. A small discussion about the autonomies of the mechanisms in the DAGs has been made.
References
[2] Johannes Textor, Benito van der Zander, Mark K. Gilthorpe, Maciej Liskiewicz, George T.H. Ellison. Robust causal inference using directed acyclic graphs: the R package ‘dagitty’. International Journal of Epidemiology 45(6):1887-1894, 2016.
[3] Judea Pearl, Causality: Models, Reasoning, and Inference, Second edition, Cambridge University Press, 2009.