Introduction
In this article, directed acyclic graphs (DAGs) from an equivalence class for an image are proposed. The reasoning behind these DAGs is explained.
Reasoning and the DAGs
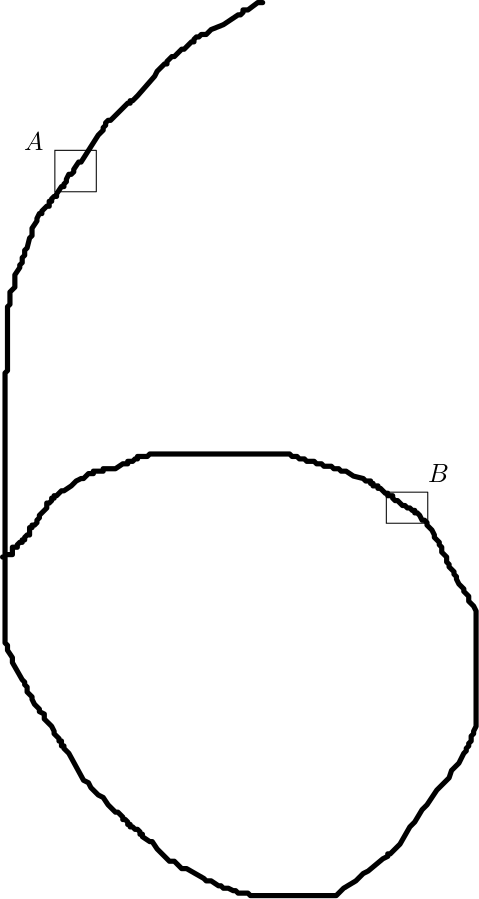
An image is a particular collection of pixels. All the pixels forming the image can be separated into disjoint subsets of pixels. Let each of such disjoint subsets be a feature of the image. The dependencies among these features will vary with the number of pixels in each feature because the visual meaning of a feature changes with the number of pixels in it. If the image is divided into features containing a big number of pixels compared to the total number of pixels in the image, then these features are expected to be dependent on each other. In the Figure 1, the rectangle $A$ contains some pixels and the rectangle $B$ contains some other pixels. The feature formed by the pixels bounded by the triangle $A$ is considered to be independent of the feature formed by the pixels bounded by the triangle $B$.
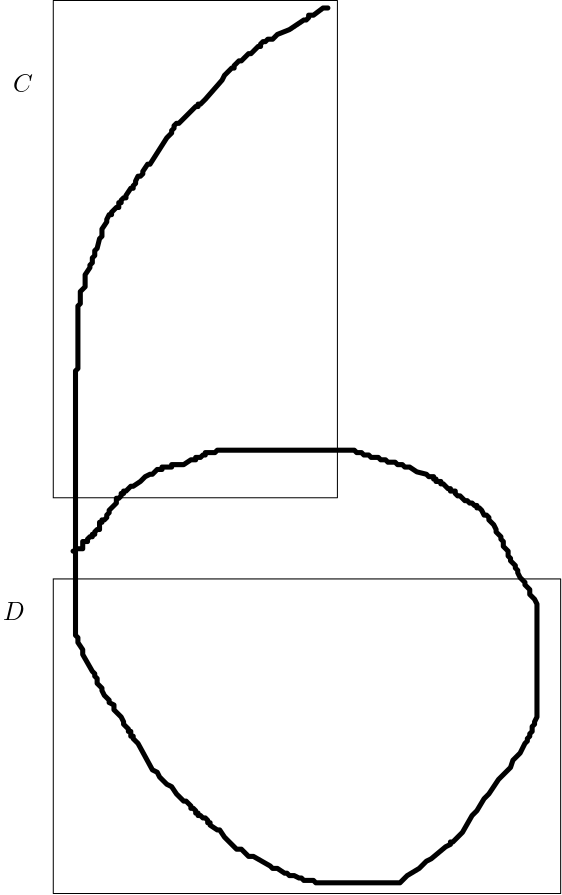
In the Figure 2, the feature formed by the pixels bounded by the rectangle $C$ and the feature formed by the pixels bounded by the rectangle $D$ are deemed to be dependent.
Let the digit be expressed using the three features displayed in the Figure 3. The features are formed by the pixels bounded by the rectangles $E$, $F$ and $G$.
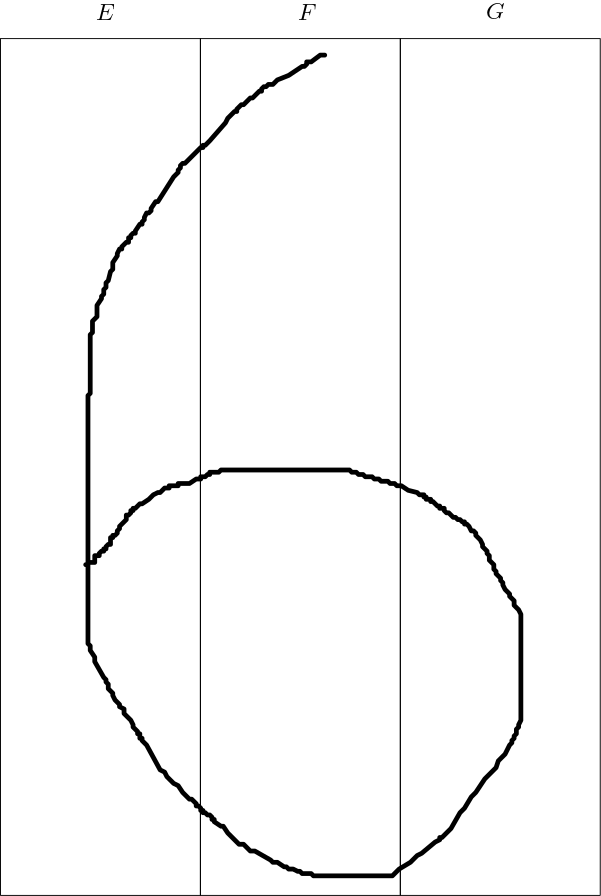
Since the number of pixels in each of the feature is big relative to the number of pixels in the image, these features are expected to be dependent on each other. How can a DAG be constructed for the digit image using three features? First of all, there should be another feature for representing the intent underlying the image. Let this feature be denoted with $I$. The intent underlying the image used so far is drawing a digit six. It can be called the label of the image, as well. $I$ should be the cause of all other three features. With the intent of drawing an image of the digit six, the first curve is drawn. Then, the second curve is drawn. Hence, the first curve is the reason for the second one. Then, the last curve is drawn according to the first and second one. Therefore, the first and the second curves are the causes for the third one. Briefly, the first curve is the cause of both the second and the third curves. The second curve is the cause of the third curve. The intent is the cause of all the curves. But, which curve is the first or the second or the third? There is no preference for which part of the image is drawn first or last. This means that there should be more than one causal models. These multiple models should represent the same set of data or the image. This situation is exactly the case for the equivalence class concept. On the page 50 of [1], an equivalence class is defined to be a set of graphs with indistinguishable d-separation implications. The graphs from the same equivalence class are different from each other but can represent the same data or the image. The conditions for belonging to the same equivalence class are sharing a common skeleton and common v-structures. The skeleton of a directed acyclic graph (DAG) is its edges regardless of the direction of those edges. The v-structures are the colliders whose parents are not adjacent. The causal models for the digit image are drawn in the Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.
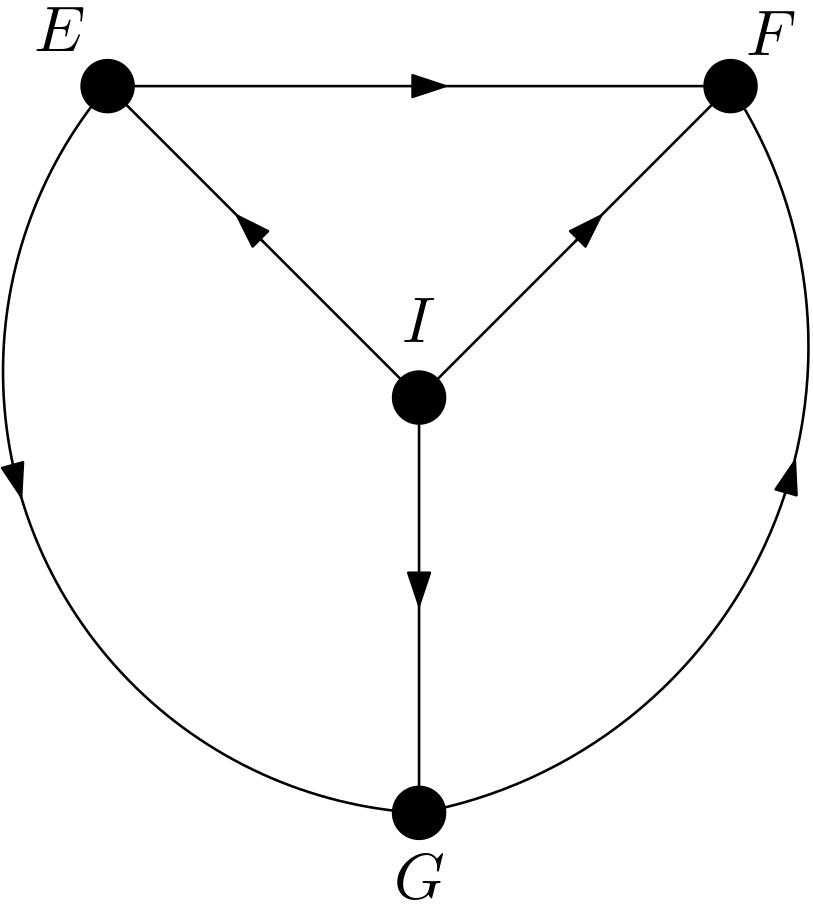
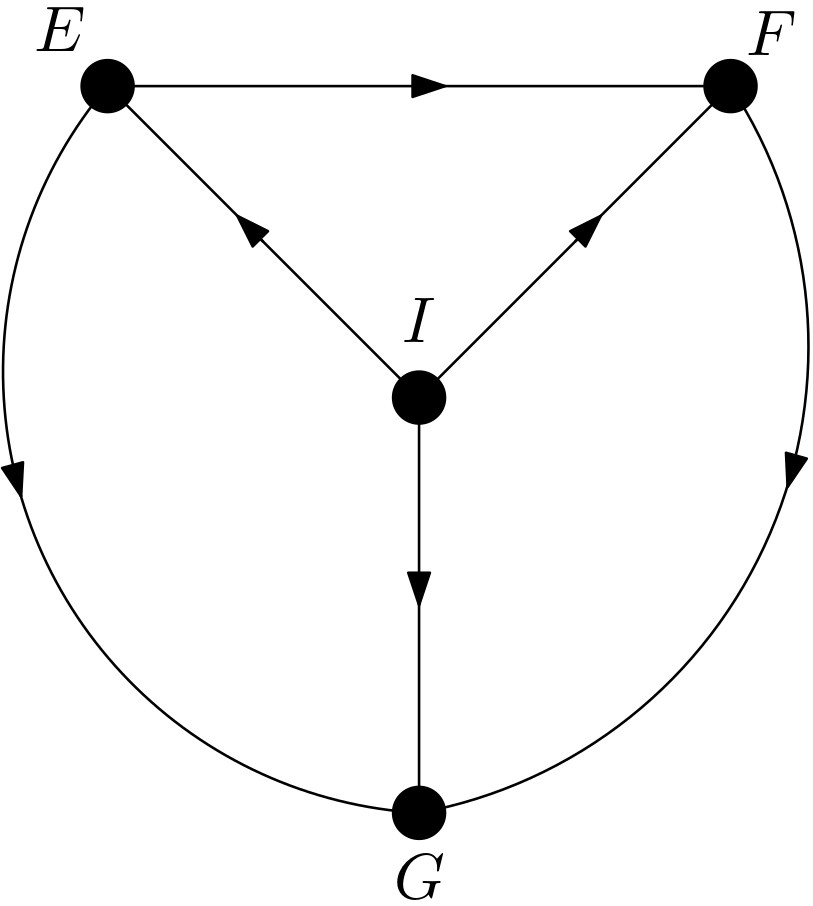
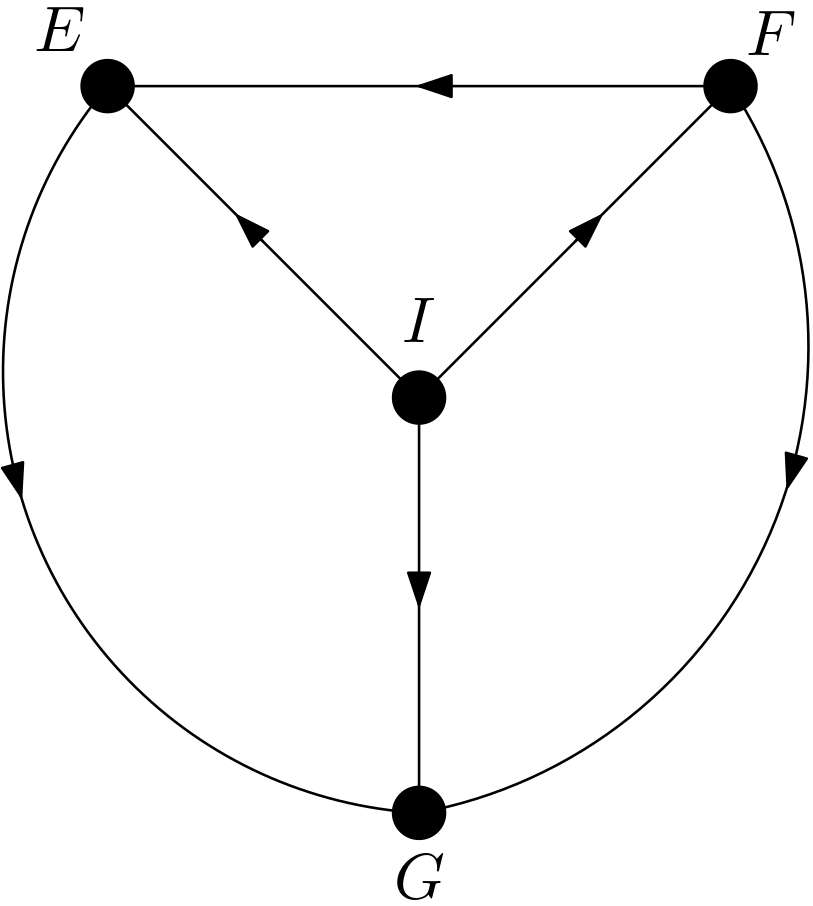
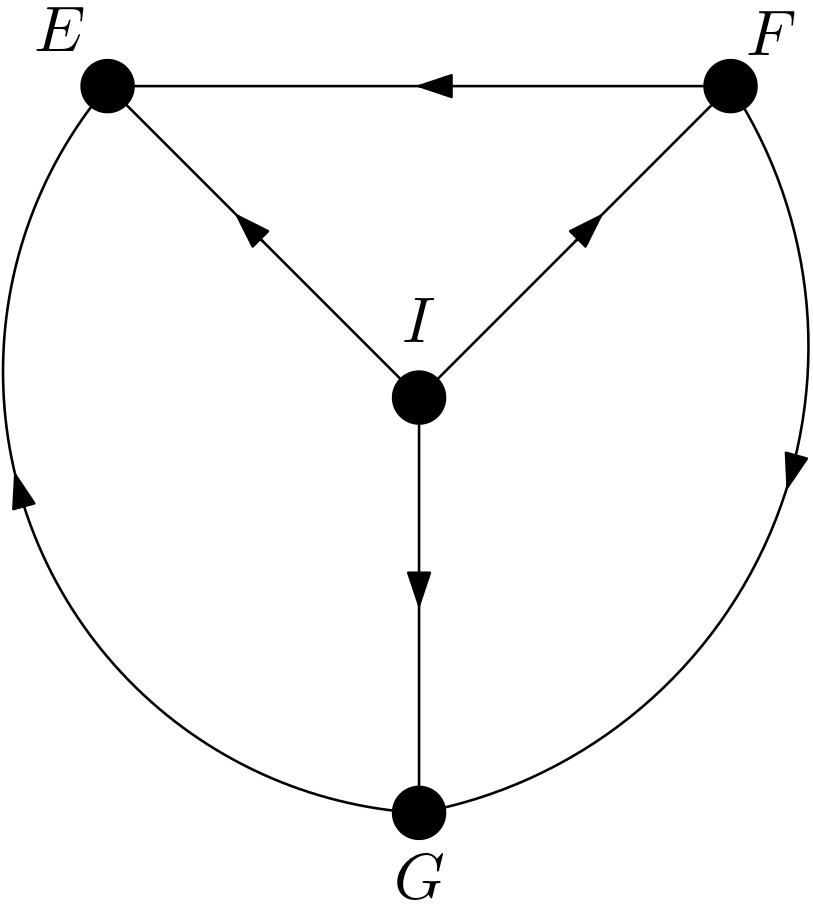
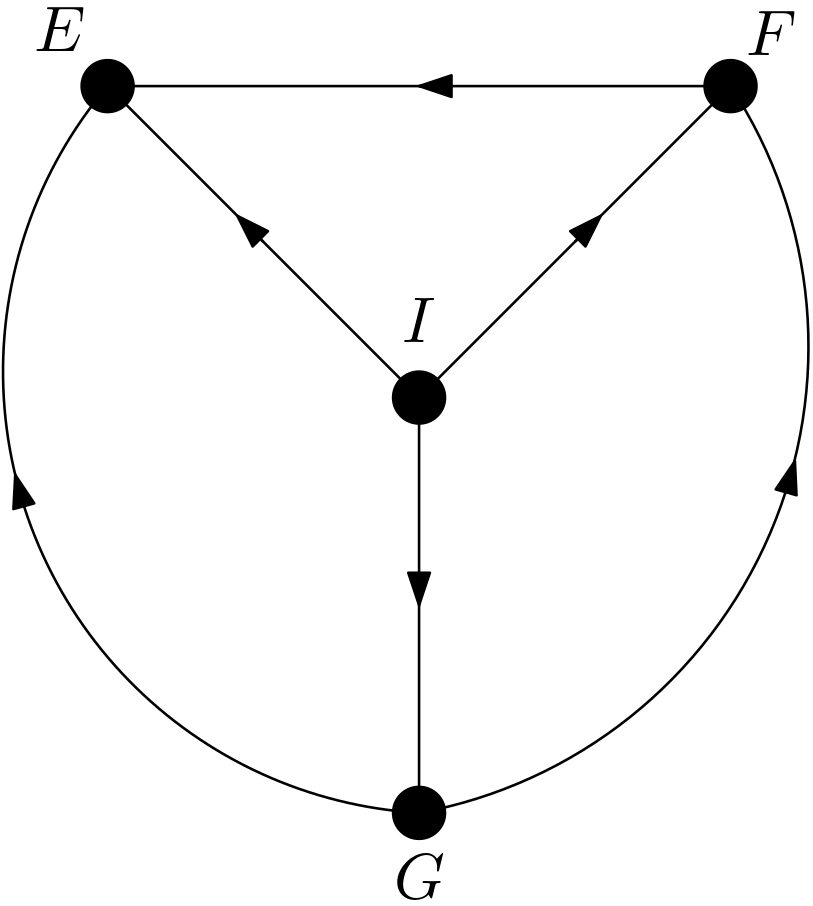
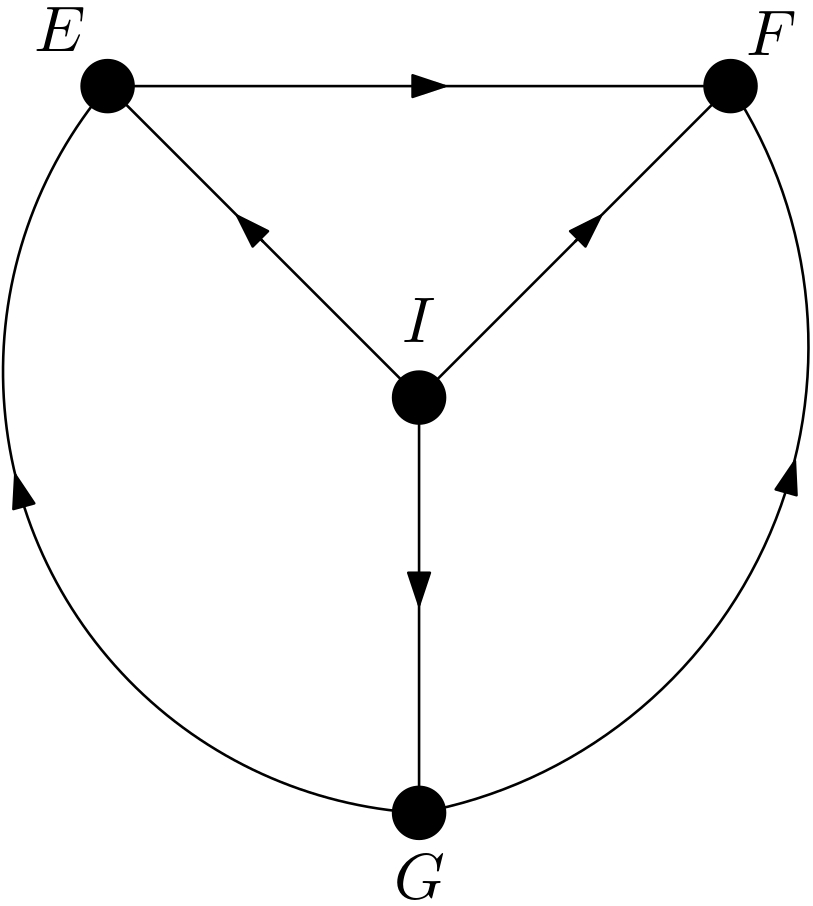
These DAGs share the same skeleton. There are no v-structures in the DAGs. So, they share the same set of v-structures, specifically no v-structures. The dependencies in these DAGs have been examined using the R package DAGitty [2] and it has been determined that there are no marginal or conditional independencies among the features. Hence, all the DAGs imply the same set of d-separation implications, specifically no marginal or conditional d-separations. The absence of marginal or conditional d-separation implications is in compliance with the above reasoning and expectation that the features should be dependent on each other since the number of pixels in each feature is relatively big.
Conclusion
DAGs from the same equivalence class for an image has been constructed. The reasoning behind these DAGs has been explained.
References
[1] Judea Pearl, Madelyn Glymour, Nicholas P. Jewell. Causal Inference In Statistics A Primer, Wiley, 2016.
[2] Johannes Textor, Benito van der Zander, Mark K. Gilthorpe, Maciej Liskiewicz, George T.H. Ellison. Robust causal inference using directed acyclic graphs: the R package ‘dagitty’. International Journal of Epidemiology 45(6):1887-1894, 2016.