Introduction
First of all, this article is best viewed in Chromium and Google Chrome browsers. Some characters are not rendered correctly in Firefox. In this article, a causal effect calculation will be carried out using the graph topology guidance. The causal effect is the causal effect of $X$ on $Y$ in the directed acyclic graph (DAG) given in the Figure 3.8 (g) on the page 92 of [1]. Its calculation has been explained in detail using the topology guidance of the DAG in the Figure 3.8 (e) in [2]. In [3], it has been shown that the DAG in the Figure 3.8 (c) can also guide the calculation of the causal effect. In this article, the details and the result of this topology guided calculation is going to be given.
Topology Guided Causal Effect Calculation
The topology guided causal effect calculation is using the know-how obtained from a DAG while finding a causal effect. If some conditions which have been explained in [2] and [3] are satisfied, then the know-how is applied in another DAG to find the target causal effect. The former is a subgraph of the latter.
The Calculation Of The Causal Effect
The DAG in which the causal effect of $X$ on $Y$ is to be found is given in the Figure 1.
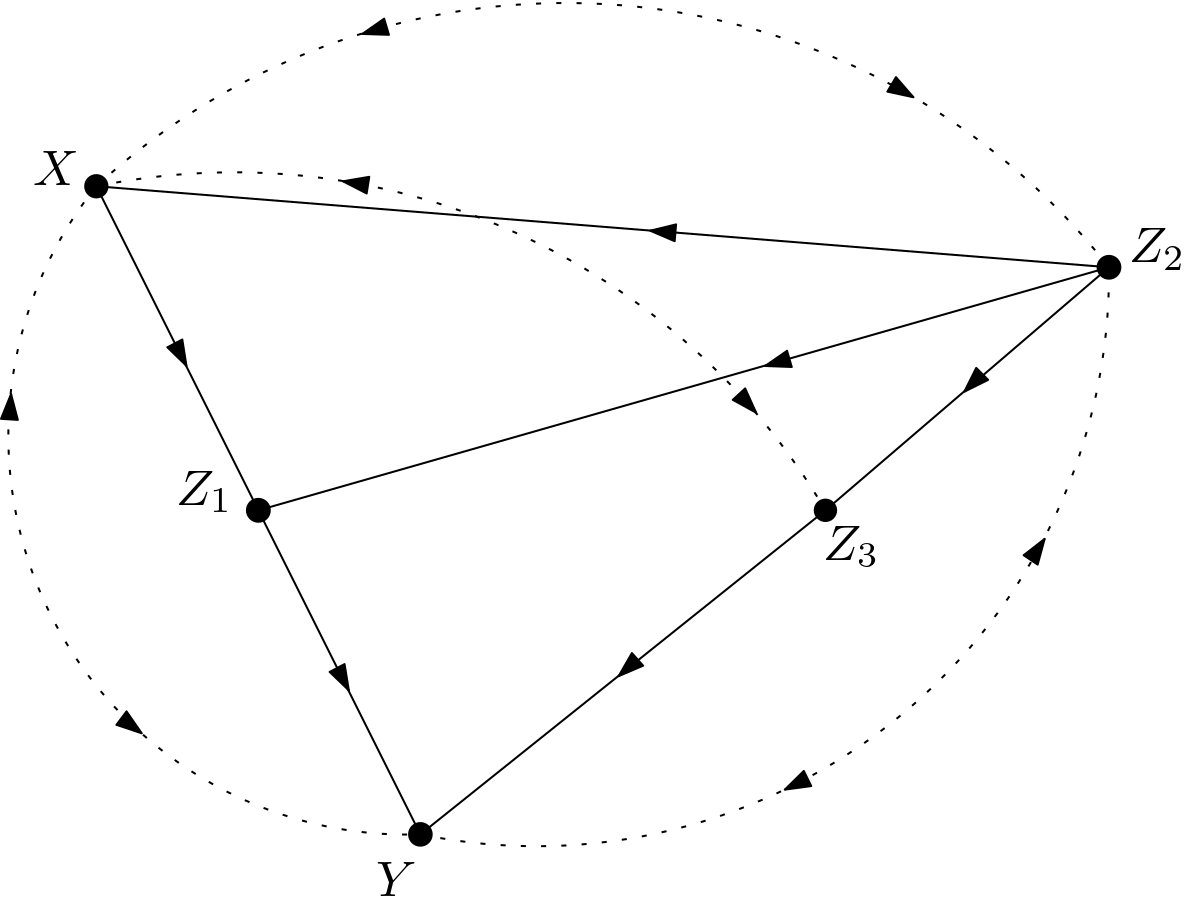
The unobserved variables are made explicit to get the DAG shown in the Figure 2. This DAG will be called $G$ from now on in this article.
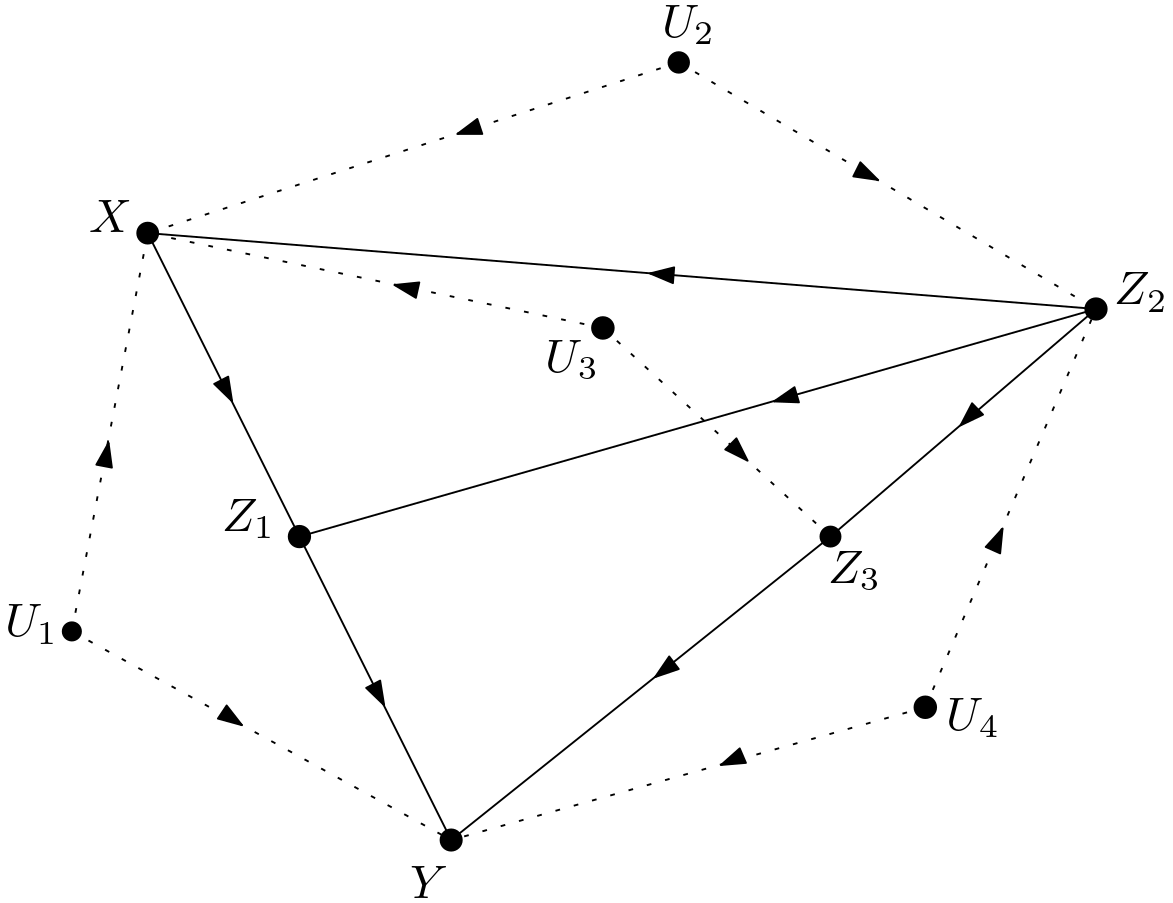
The DAG which will guide the calculation of $p\left(y|do\left(x\right)\right)$ is shown in the Figure 3.
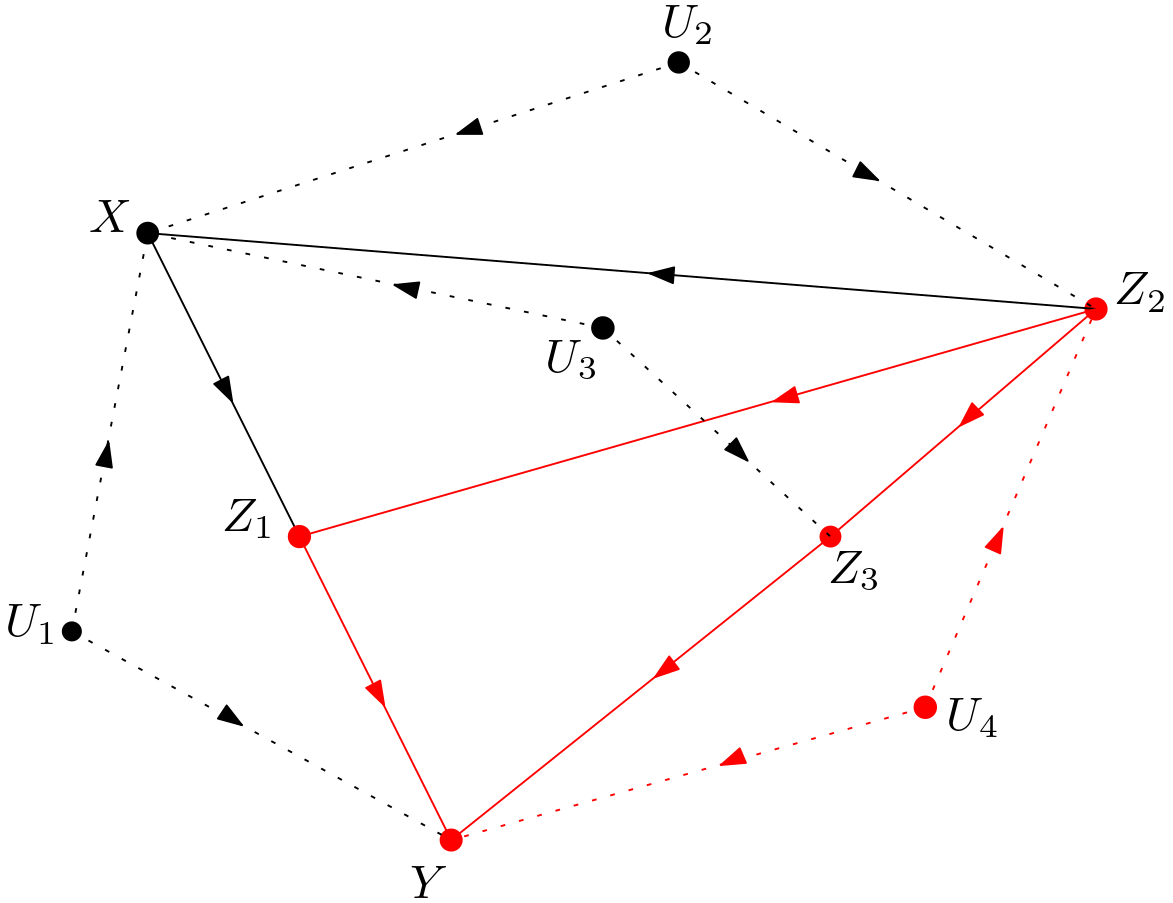
The subgraph of $G$ which is the guiding DAG is shown in red in the Figure 4.
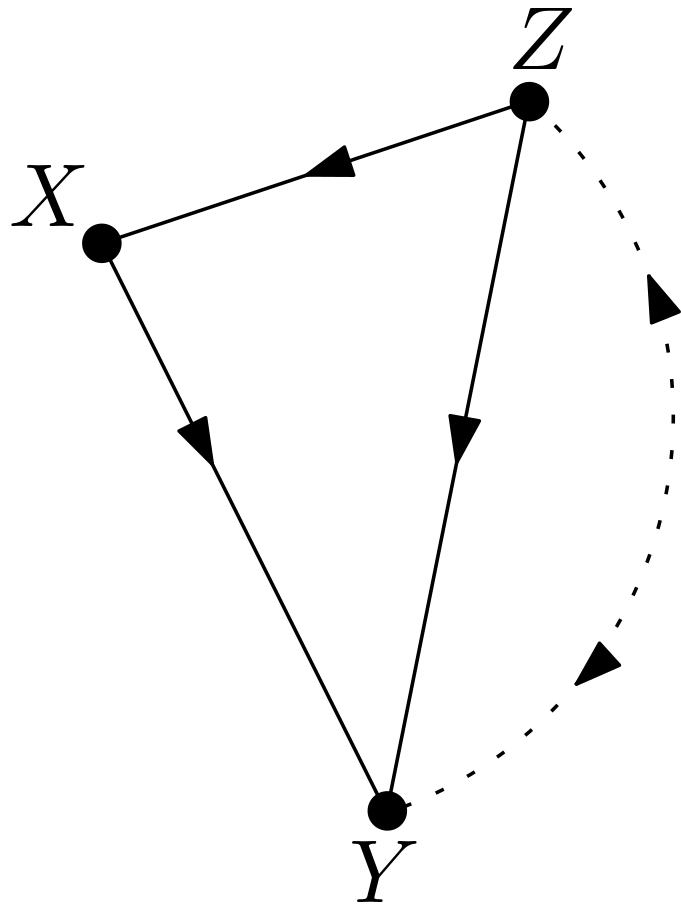
In the Figure 5, the guiding DAG is drawn alone. This DAG will be called $D$ from now on in this article. In $D$, the causal effect of $Z_{1}$ on $Y$, i.e. $p\left(y|do\left(z_{1}\right)\right)$, is identifiable. In [3], it has been shown that the know-how for $p\left(y|do\left(z_{1}\right), z_{2}\right)$ is required.
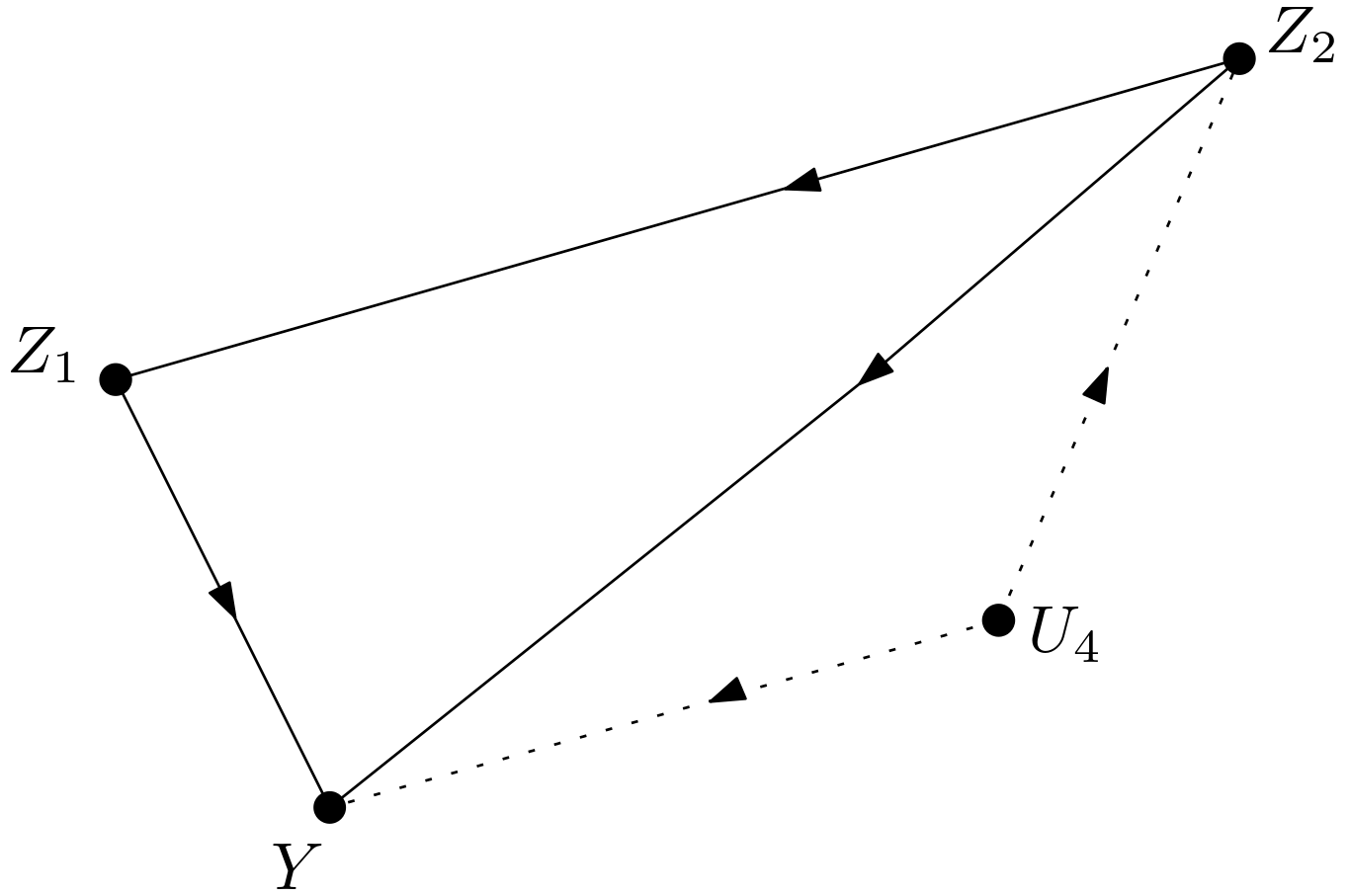
The rules of do-calculus will first be used. Can the intervention on $Z_{1}$ be replaced with observing $Z_{1}$? Is $p\left(y|do\left(z_{1}\right), z_{2}\right)$ equal to $p\left(y|z_{1}, z_{2}\right)$? For this replacement or equality to be valid, $Y$ and $Z_{1}$ must be conditionally d-separated given $Z_{2}$ in the graph $D_{\underline{Z_{1}}}$. $D_{\underline{Z_{1}}}$ is shown in the Figure 6.
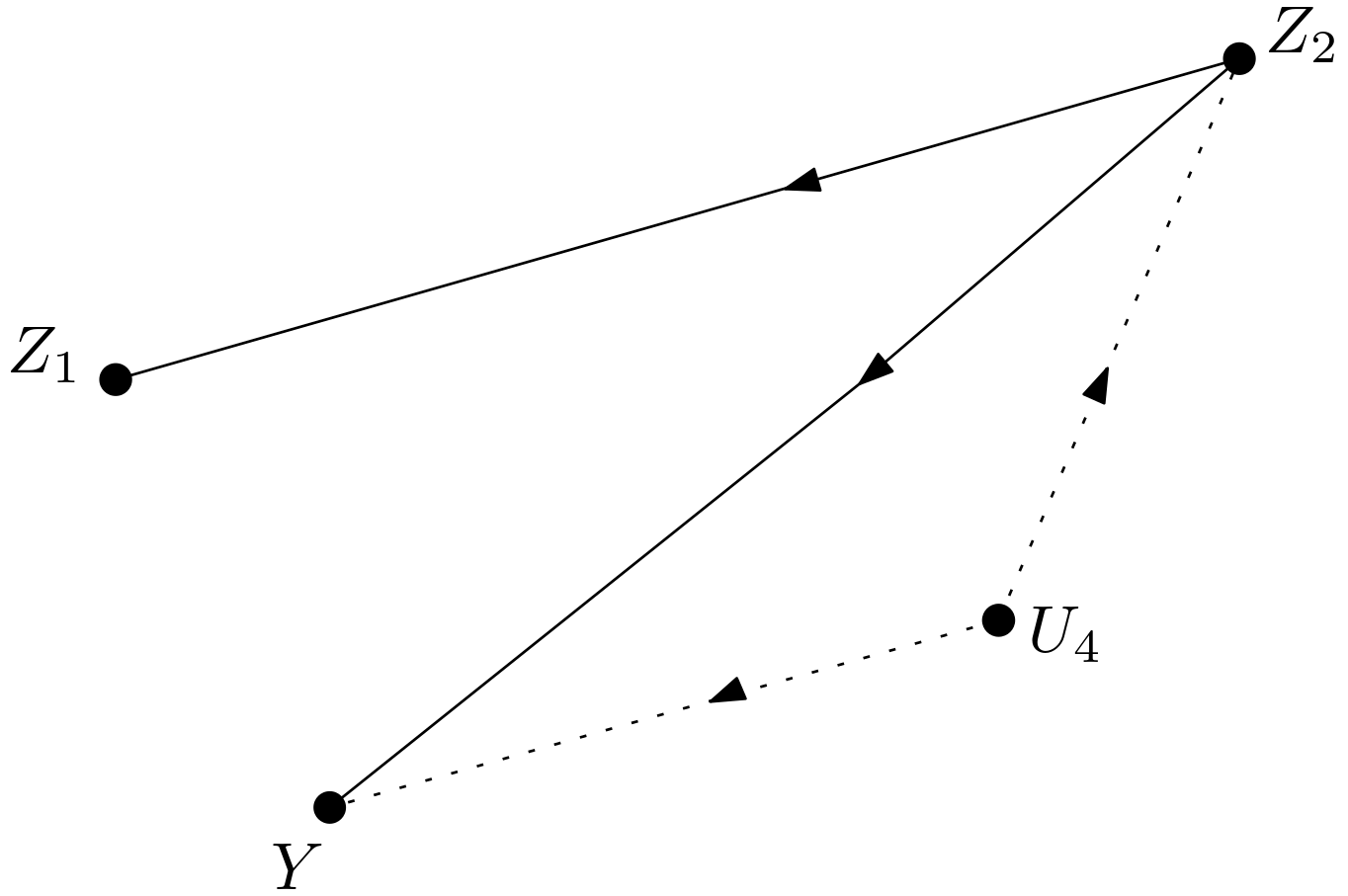
There are two paths from $Z_{1}$ to $Y$. They are as follows: \begin{equation} \begin{array}{l} 1) \, Z_{1} \leftarrow Z_{2} \rightarrow Y \newline 2) \, Z_{1} \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y \end{array} \end{equation} These paths are blocked due to conditioning on $Z_{2}$. Hence, $Y$ and $Z_{1}$ are conditionally d-separated given $Z_{2}$ in the graph $D_{\underline{Z_{1}}}$, which means that $p\left(y|do\left(z_{1}\right), z_{2}\right)$ can be written as $p\left(y|z_{1}, z_{2}\right)$. Hence, $p\left(y|do\left(z_{1}\right), z_{2}\right)$ in the equation (27) in [3] can be replaced with $p\left(y|z_{1}, z_{2}\right)$.
Conclusion
The causal effect calculation by the guidance of the DAG in the Figure 5 has been carried out.
References
[1] Judea Pearl, Causality: Models, Reasoning and Inference, Cambridge University Press, 2009.