Introduction
First of all, this article is best viewed in Chromium and Google Chrome browsers. Some characters are not rendered correctly in Firefox. In this article, some graphs are examined to determine if they can be utilized in calculating a causal effect in a given directed acyclic graph (DAG). Each graph is studied to detect if only this graph is enough to calculate the causal effect. The examined graphs are the (b), (c) and (d) parts of the Figure 3.8 on page 92 of [1]. The DAG for which the causal effect is to be calculated is the (g) part of the Figure 3.8 on page 92 of [1].
The Topology Guided Causal Effect Calculation
In the topology guided causal effect calculation, a subgraph of the DAG under investigation is examined to determine if it is appropriate to be used in the calculation of the causal effect. If it is appropriate, then the know-how from that subgraph is utilized. The graph in the Figure 3.8 (e) is said to be suitable in [1] for the calculation of $p\left(y|do\left(x\right)\right)$ in the graph (g) of the Figure 3.8. In [2], it is shown in detail how the graph in the Figure 3.8 (e) can be used to calculate this causal effect. Each one of the graphs in the Figure 3.8 (b), (c) and (d) is to be checked if only the checked graph is enough to calculate the causal effect in the graph (g) of the Figure 3.8.
The Examination of The Graphs
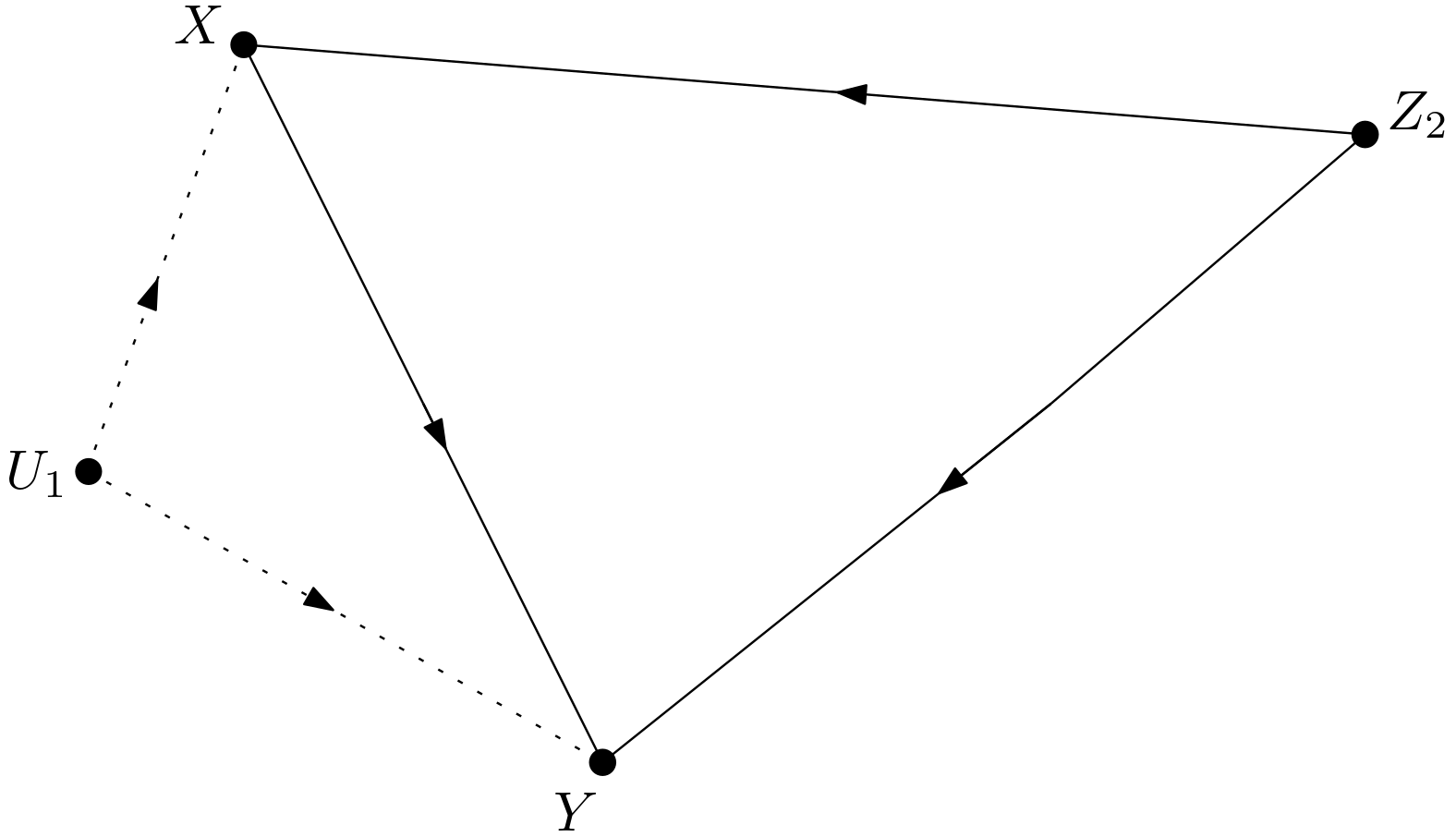
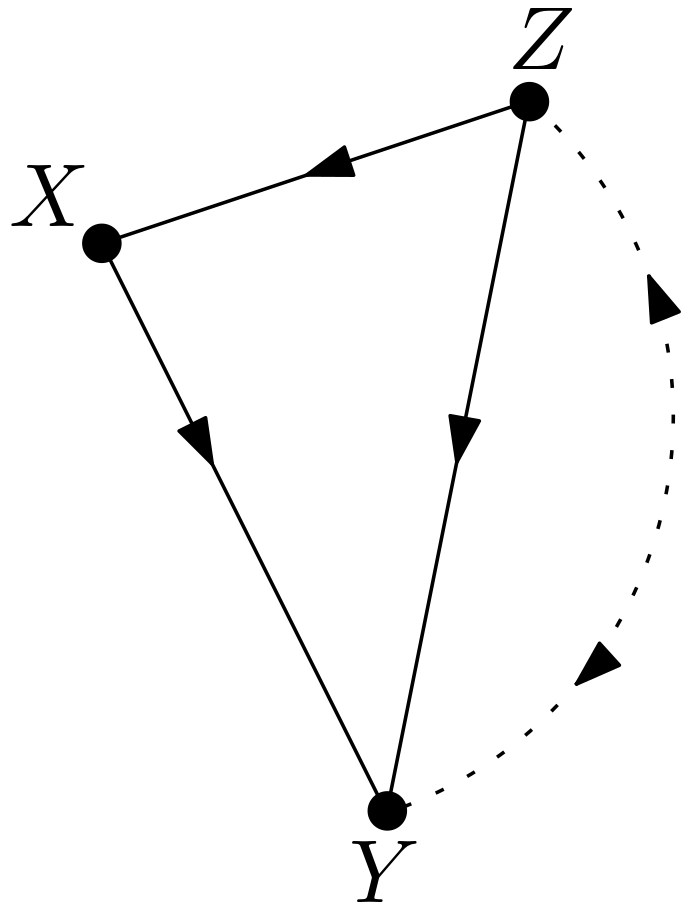
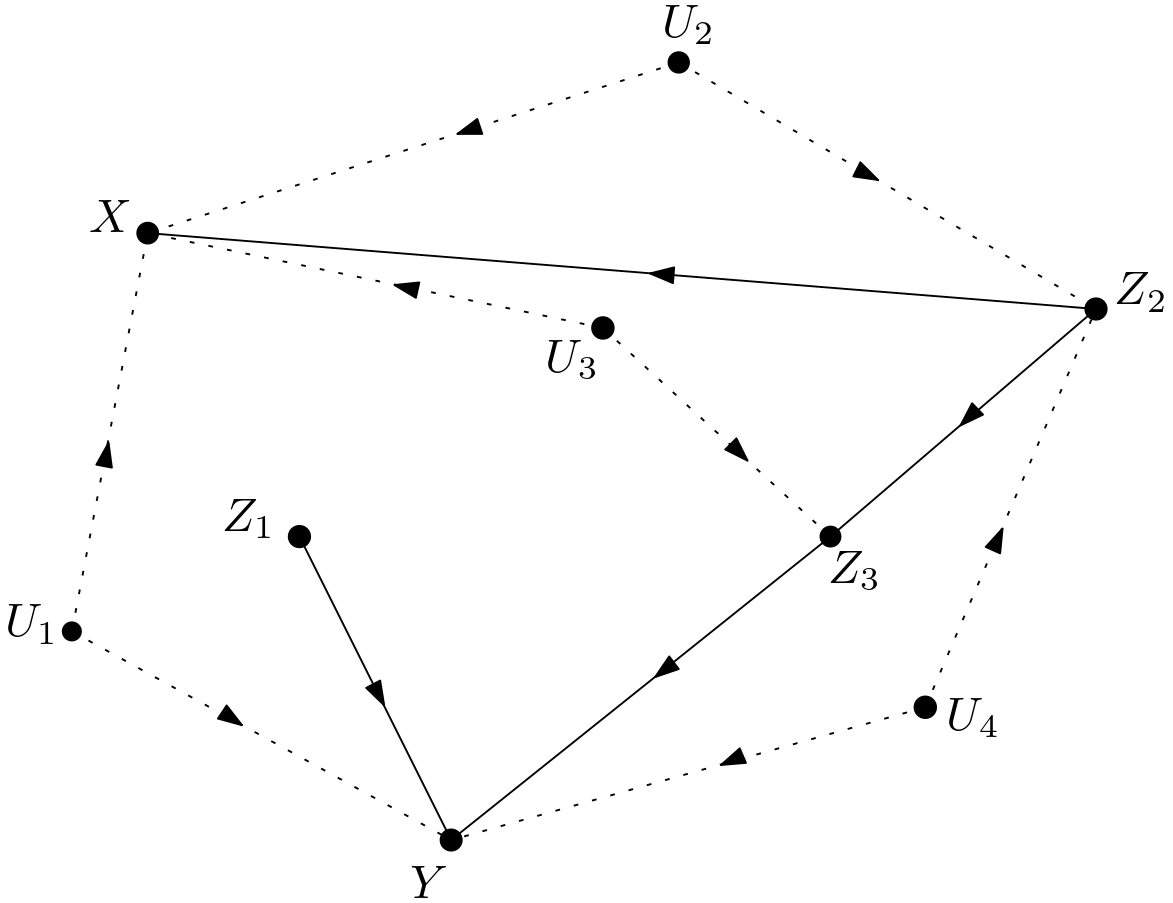
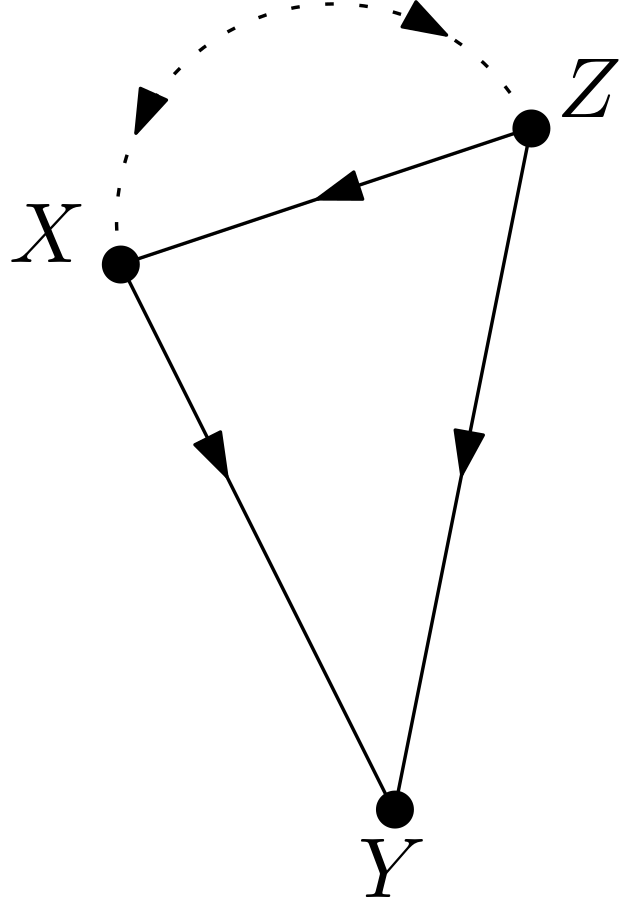
The causal effect of $X$ on $Y$ is to be calculated for the DAG in the Figure 1.
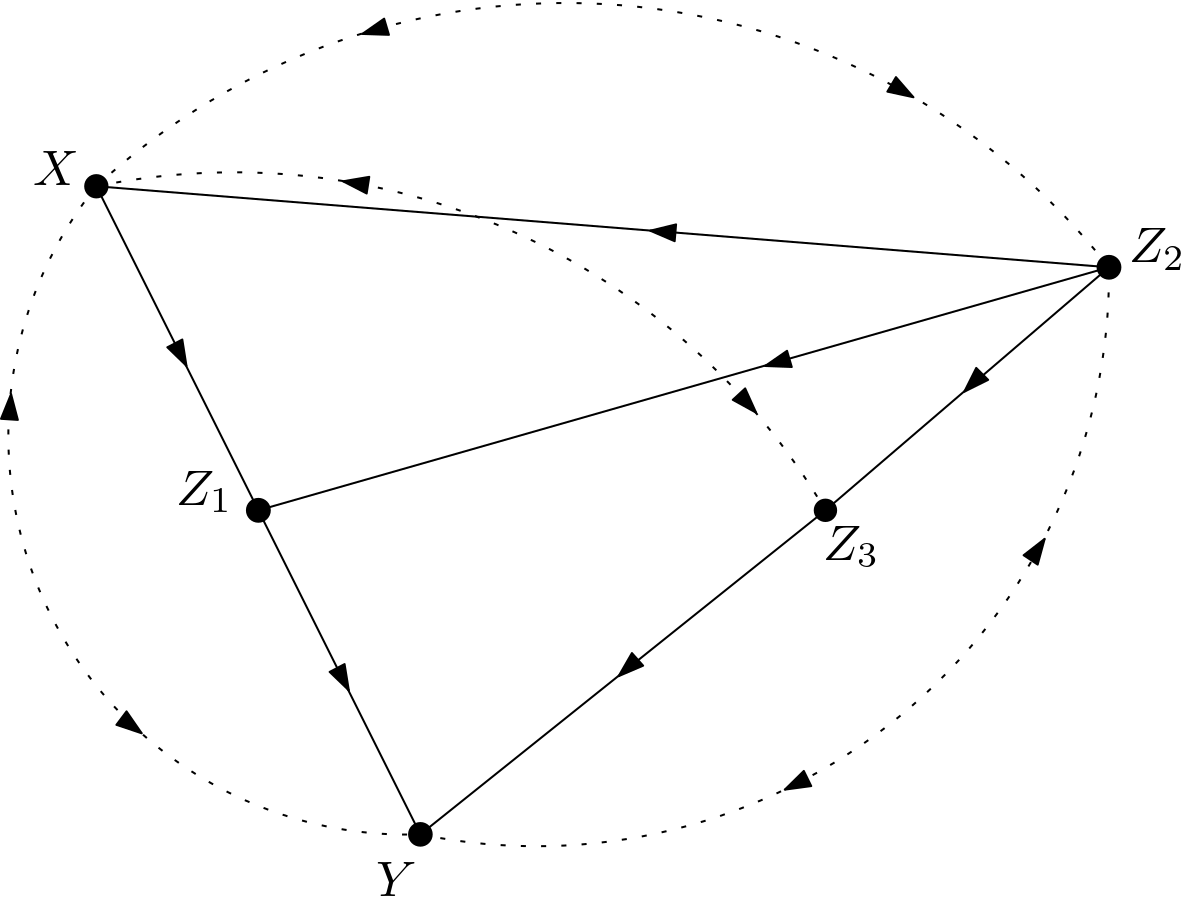
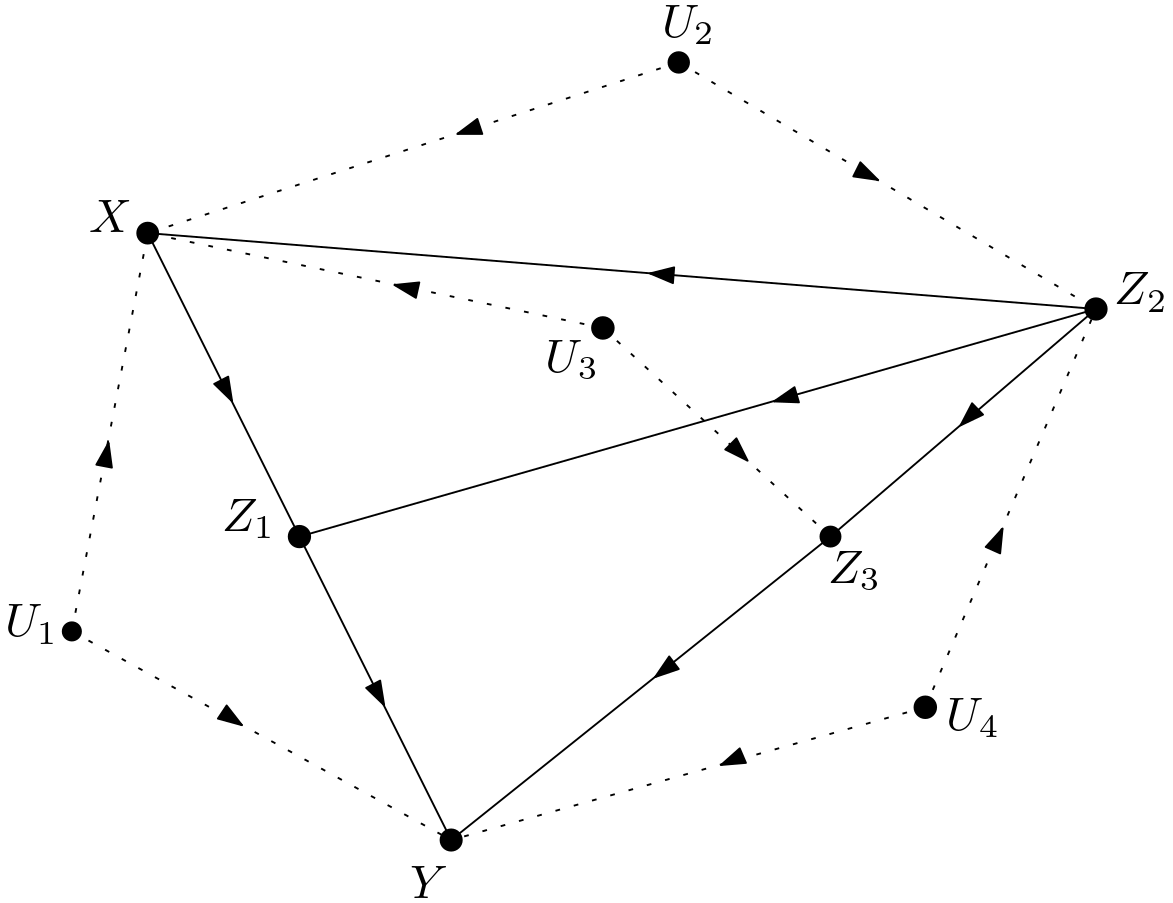
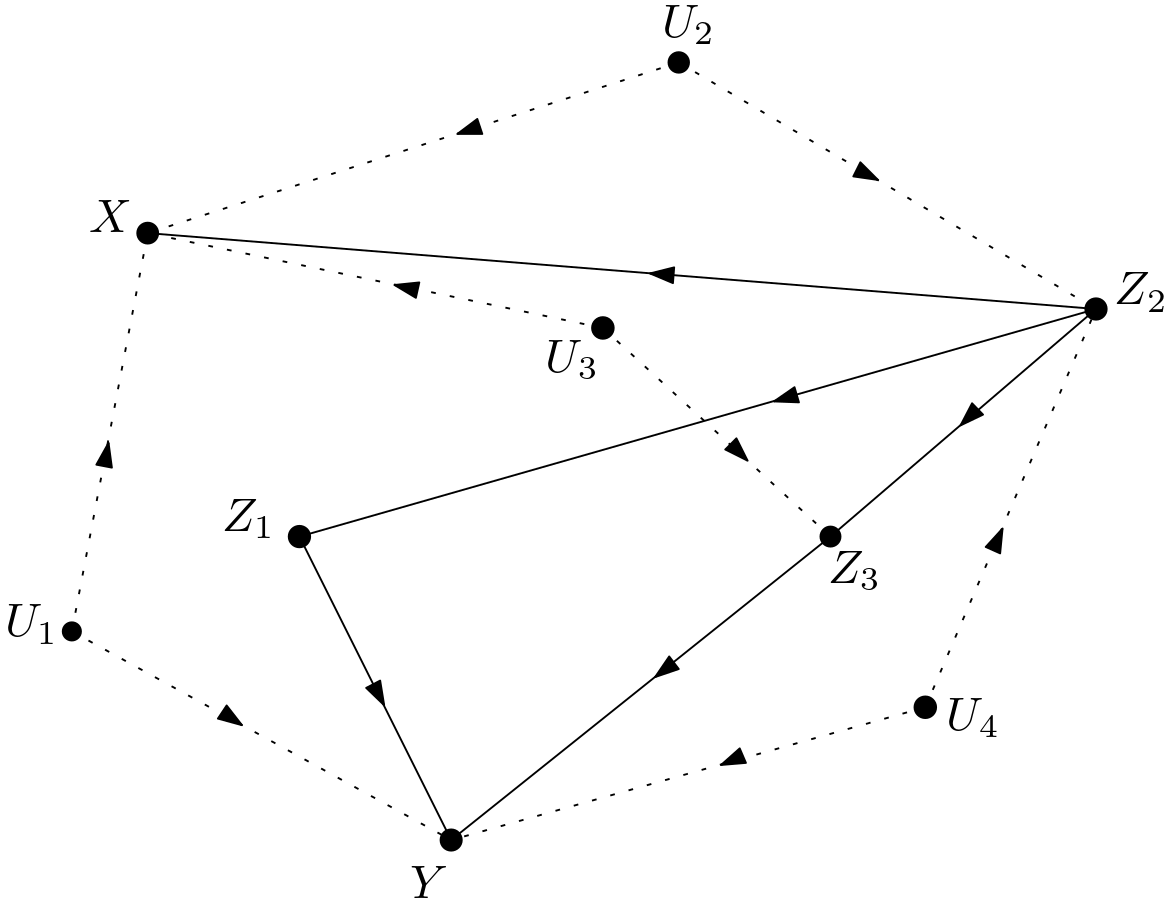
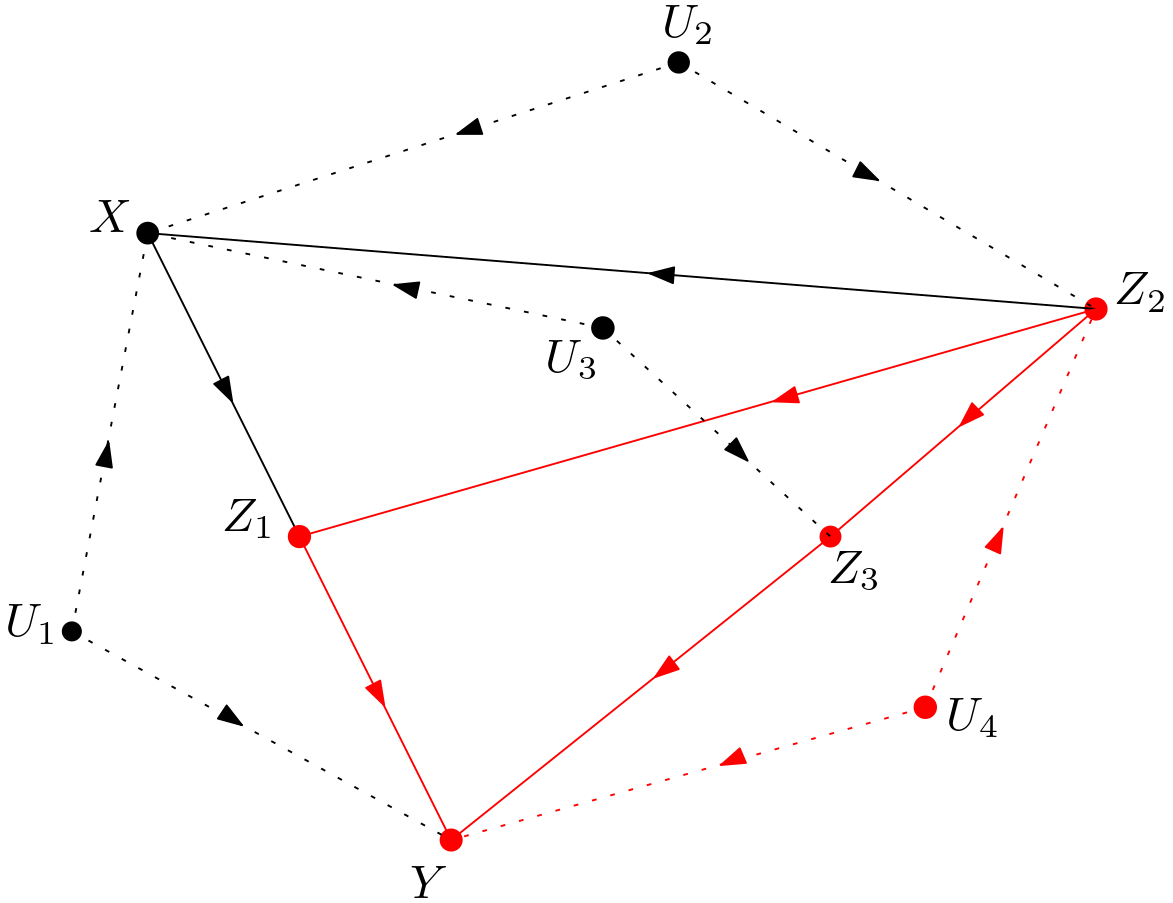
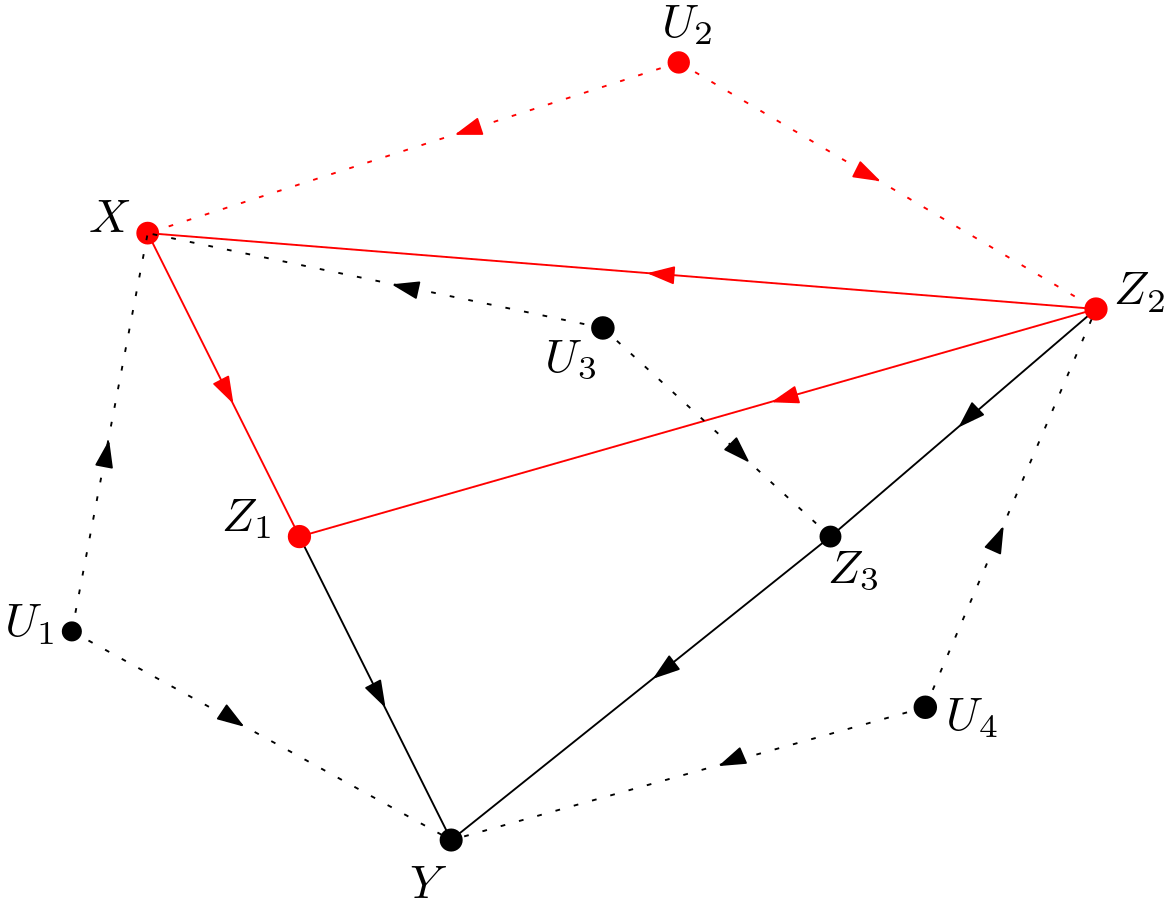
The unobserved variables are made explicit to obtain the version shown in the Figure 2. This graph will be called $G$ throughout the article.
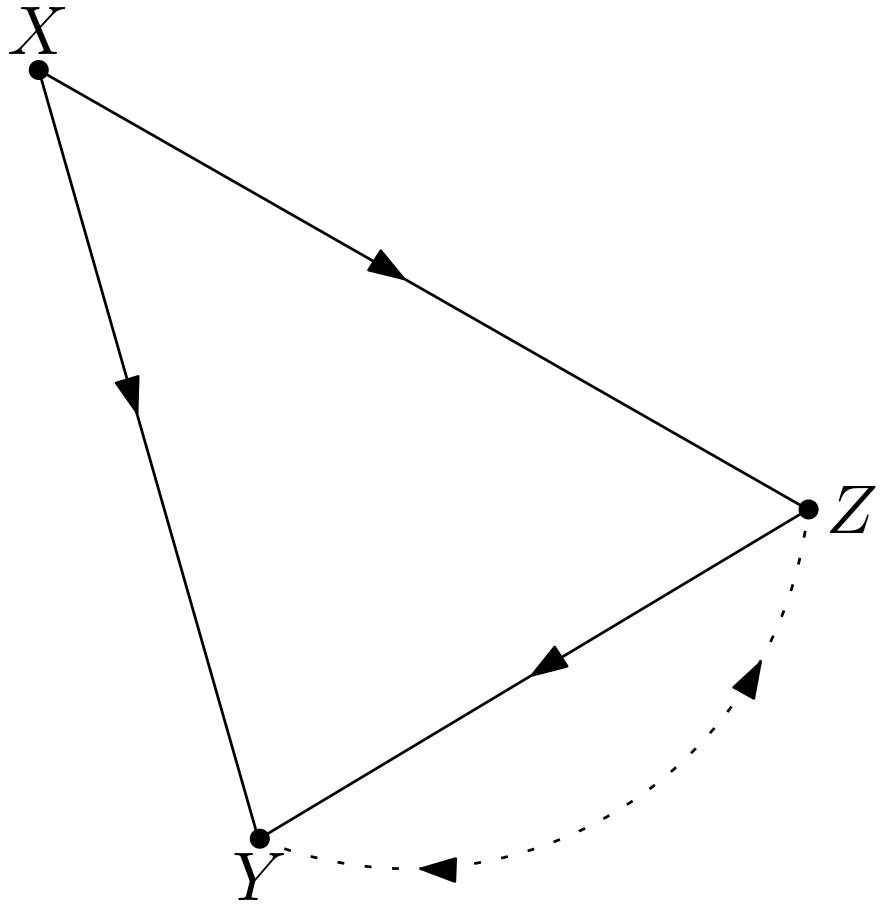
The graph in the Figure 3.8 (b) of [1] is drawn in the Figure 3.
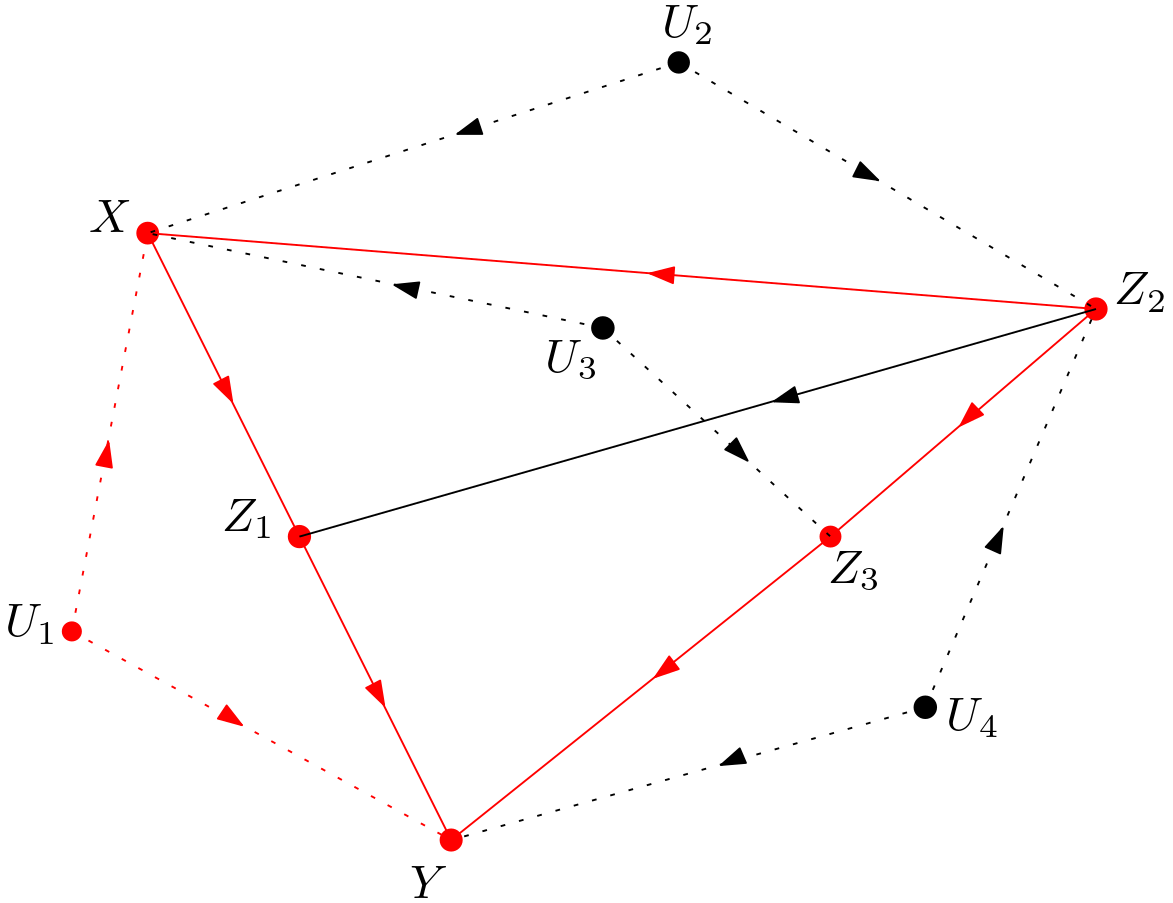
The subgraph of $G$ matching to this graph is indicated in red in the Figure 4.
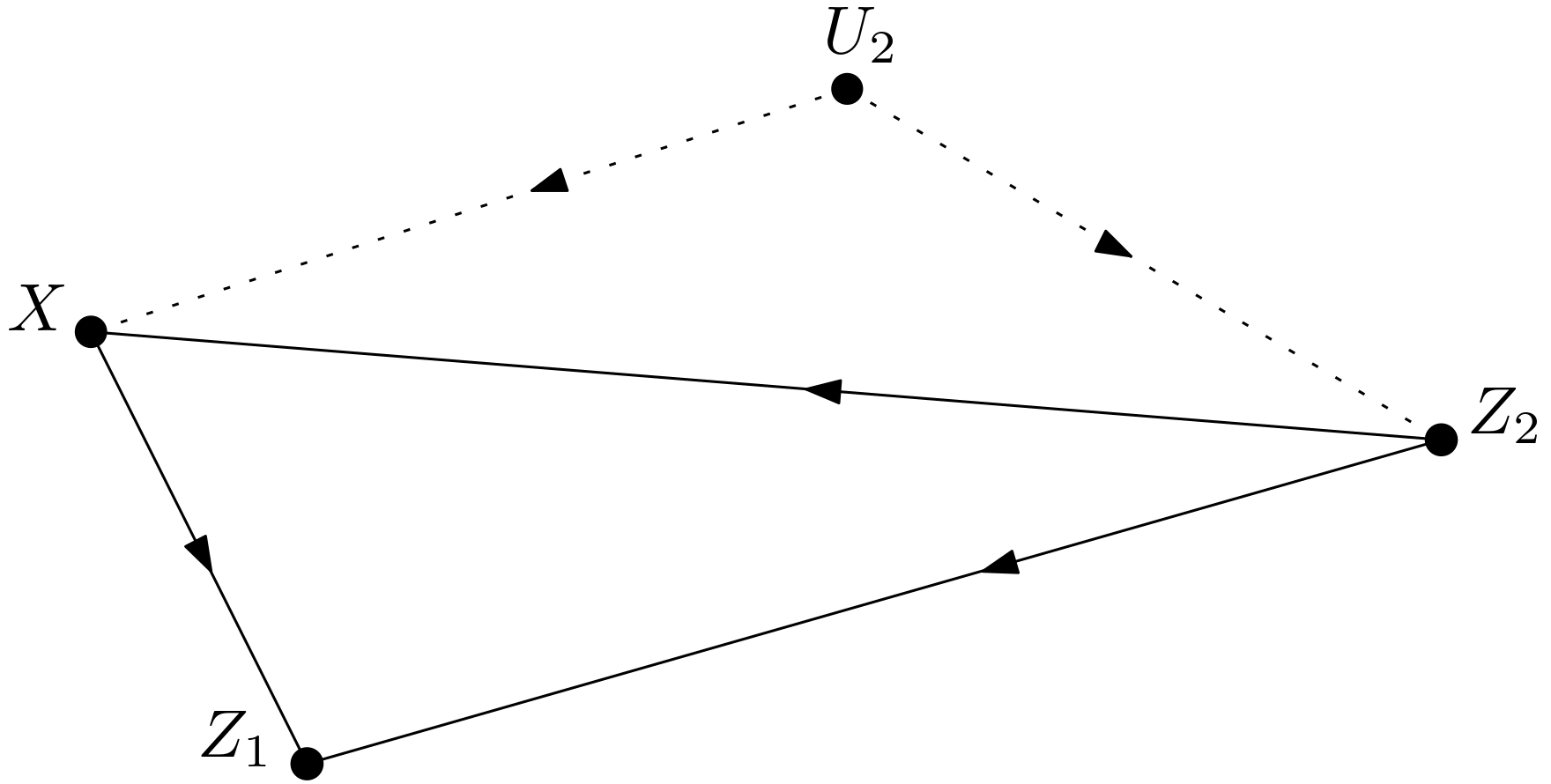
Let it be studied if only the graph in the Figure 5 is enough to help determining the causal effect of $X$ on $Y$ in $G$. In the graph, the causal effect of $Z_{2}$ on $Y$ is identifiable. The causal effect of $Z_{2}$ on $Y$ is due to the post-intervention distribution which is valid in the mutilated graphs formed by removing arrows entering $Z_{2}$. If the dependencies in the mutilated graphs happen to be similar, then the causal effect of $Z_{2}$ on $Y$ in $G$ can be calculated using the know-how from the graph in the Figure 5.
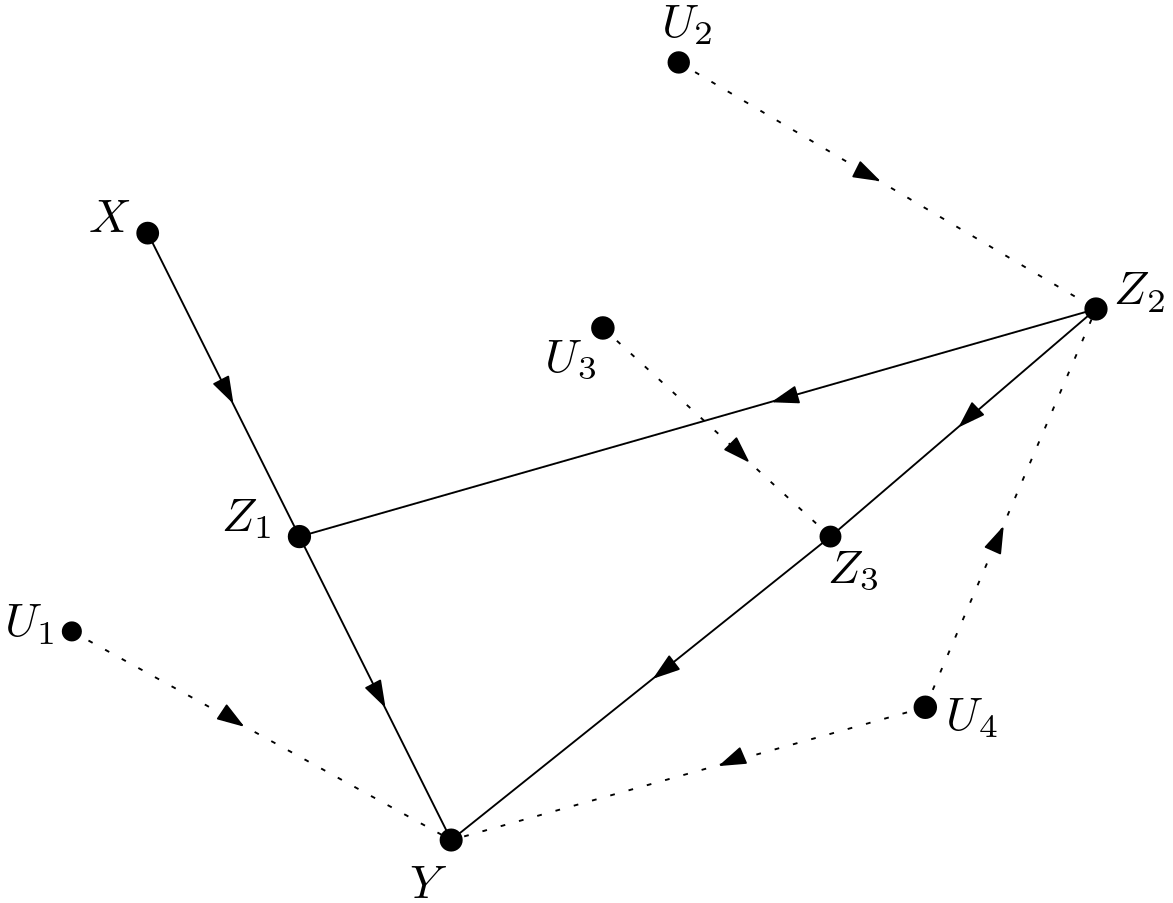
Let it be assumed that the dependencies in the mutilated graphs were similar. Then, $p\left(y|do\left(z_{2}\right)\right)$ could be calculated in $G$. That is why this causal quantity should be incorporated into the calculation of $p\left(y|do\left(x\right)\right)$. This can be done using the following expansion: \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{2}}p\left(y,z_{2}|do\left(x\right)\right)=\sum_{z_{2}}\frac{p\left(y,z_{2}|do\left(x\right)\right)}{p\left(z_{2}|do\left(x\right)\right)}p\left(z_{2}|do\left(x\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{2}}p\left(y|z_{2},do\left(x\right)\right)p\left(z_{2}|do\left(x\right)\right) \label{expansion_one} \end{equation} In the expansion above, $p\left(y|z_{2},do\left(x\right)\right)$ term should be converted to $p\left(y|do\left(z_{2}\right)\right)$. Can the intervention on $X$ be replaced with observing $X$? Is $p\left(y|z_{2},do\left(x\right)\right)$ equal to $p\left(y|z_{2},x\right)$? This is possible if $Y$ and $X$ are conditionally d-separated given $Z_{2}$ in the graph $G_{\underline{X}}$. $G_{\underline{X}}$ is shown in the Figure 6. $Y$ and $X$ can never be conditionally d-separated given $Z_{2}$ in the graph $G_{\underline{X}}$ due to the following unblocked paths: \begin{equation} \begin{array}{l} 1) \, X \leftarrow U_{1} \rightarrow Y \newline 2) \, X \leftarrow U_{3} \rightarrow Z_{3} \rightarrow Y \end{array} \end{equation} Therefore, $p\left(y|z_{2},do\left(x\right)\right)$ cannot be equal to $p\left(y|z_{2},x\right)$. Can these paths be blocked by conditioning on either $Z_{1}$ or $Z_{3}$? $X \leftarrow U_{3} \rightarrow Z_{3} \rightarrow Y$ can be blocked by conditioning on $Z_{3}$. However, this is not enough since $X \leftarrow U_{1} \rightarrow Y$ can never be blocked due to the unobserved variable $U_{1}$. As a result, $p\left(y|z_{2}, do\left(x\right)\right)$ cannot be written as $p\left(y|z_{2}, x\right)$.
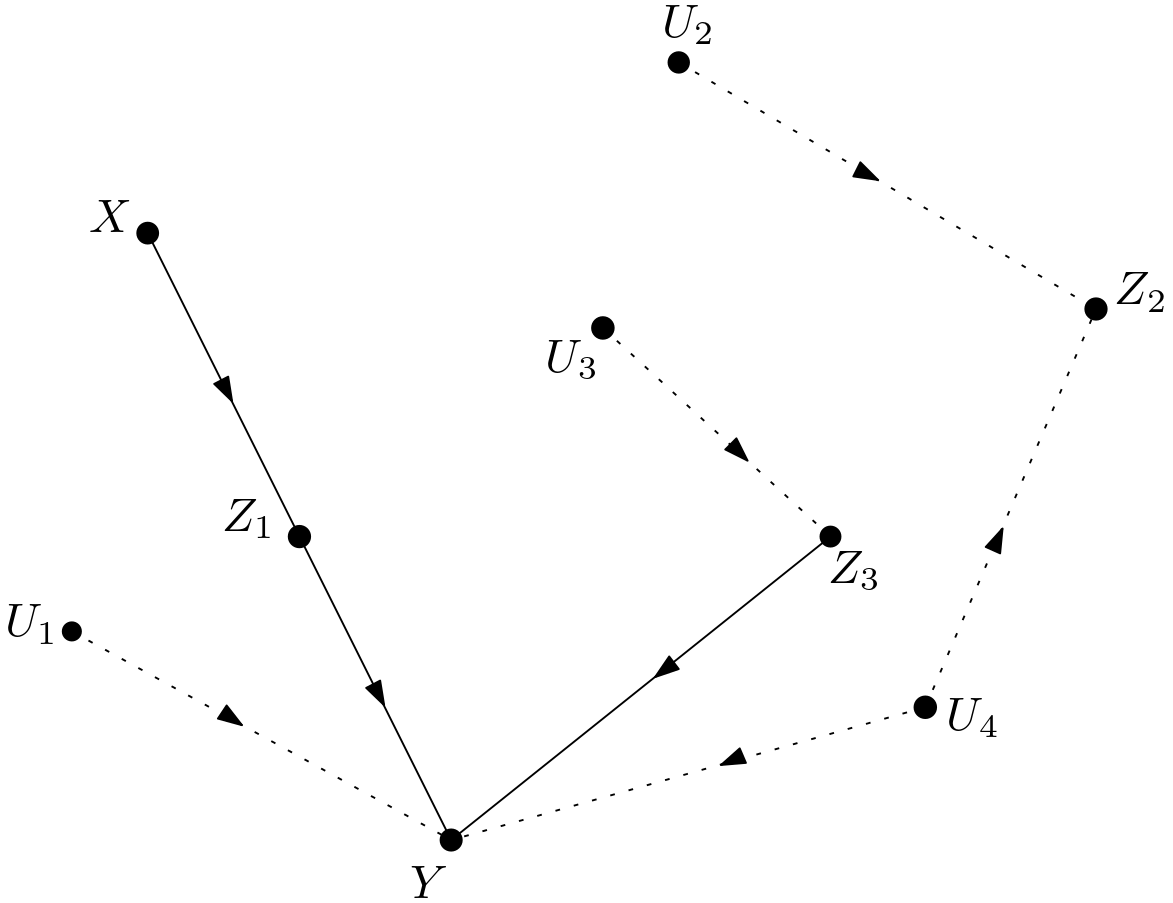
For $p\left(y|z_{2},do\left(x\right)\right)$ in the equation (\ref{expansion_one}), can the intervention on $X$ be removed, i.e. is $p\left(y|z_{2},do\left(x\right)\right)$ equal to $p\left(y|z_{2}\right)$? The removal is possible if $Y$ and $X$ are conditionally d-separated given $Z_{2}$ in the graph $G_{\overline{X\left(Z_{2}\right)}}$. $X\left(Z_{2}\right)$ represents $X$ which are not ancestors of $Z_{2}$ in $G$. $X$ is not an ancestor of $Z_{2}$, which means that $G_{\overline{X\left(Z_{2}\right)}}=G_{\overline{X}}$. $G_{\overline{X}}$ is shown in the Figure 7. As can easily be seen from the figure, $Y$ and $X$ are d-connected through the path $X \rightarrow Z_{1} \rightarrow Y$ in the graph $G_{\overline{X}}$. Hence, $p\left(y|z_{2},do\left(x\right)\right)$ cannot be equal to $p\left(y|z_{2}\right)$. Can this d-connection be disturbed by conditioning on either $Z_{1}$ or $Z_{3}$? If $Z_{1}$ is conditioned on, then $Y$ and $X$ might seem to become d-separated. However, this d-separation is not possible because $X$ is an ancestor of $Z_{1}$ implying $G_{\overline{X\left(Z_{1}, Z_{2}\right)}}=G$. In $G$, $Y$ and $X$ are not conditionally d-separated given $Z_{1}$ and $Z_{2}$ meaning $p\left(y|z_{1}, z_{2},do\left(x\right)\right) \neq p\left(y|z_{1}, z_{2}\right)$. Conditioning on $Z_{3}$ cannot disturb the fact that $Y$ and $X$ are d-connected in $G_{\overline{X}}$. As a result, $p\left(y|z_{2}, do\left(x\right)\right)$ cannot be written as $p\left(y|z_{2}\right)$.
For $p\left(y|z_{2},do\left(x\right)\right)$ in the equation (\ref{expansion_one}), can observing $Z_{2}$ be replaced with an intervention on $Z_{2}$, i.e. is $p\left(y|z_{2},do\left(x\right)\right)$ equal to $p\left(y|do\left(z_{2}\right),do\left(x\right)\right)$? The replacement or the equality is achievable if $Y$ and $Z_{2}$ are conditionally d-separated given $X$ in the graph $G_{\overline{X}\underline{Z_{2}}}$. The graph $G_{\overline{X}\underline{Z_{2}}}$ is given in the Figure 8. $Y$ and $Z_{2}$ aren’t conditionally d-separated given $X$ in the graph $G_{\overline{X}\underline{Z_{2}}}$ because of the unblocked path $Z_{2} \leftarrow U_{4} \rightarrow Y$. There is no way of unblocking this path because $U_{4}$ is an unobserved variable. Therefore, $p\left(y|z_{2},do\left(x\right)\right)$ cannot be equal to $p\left(y|do\left(z_{2}\right),do\left(x\right)\right)$.
After checking the ways of converting $p\left(y|z_{2},do\left(x\right)\right)$ in the equation (\ref{expansion_one}) to $p\left(y|do\left(z_{2}\right)\right)$, it has been determined that this conversion is not possible. Hence, the know-how from the graph in the Figure 5 cannot be used to calculate the causal effect in $G$ even if the dependencies in the mutilated graphs were similar.
It is the turn of the graph in the Figure 3.8 (c) of [1]. It is drawn in the Figure 9.
The subgraph of $G$ matching to this graph is shown in the Figure 10. If the dependencies in the mutilated form of this graph and that of $G$ are similar, then the know-how from the graph in the Figure 11 can be used to calculate the causal effect of $Z_{1}$ on $Y$ in $G$.
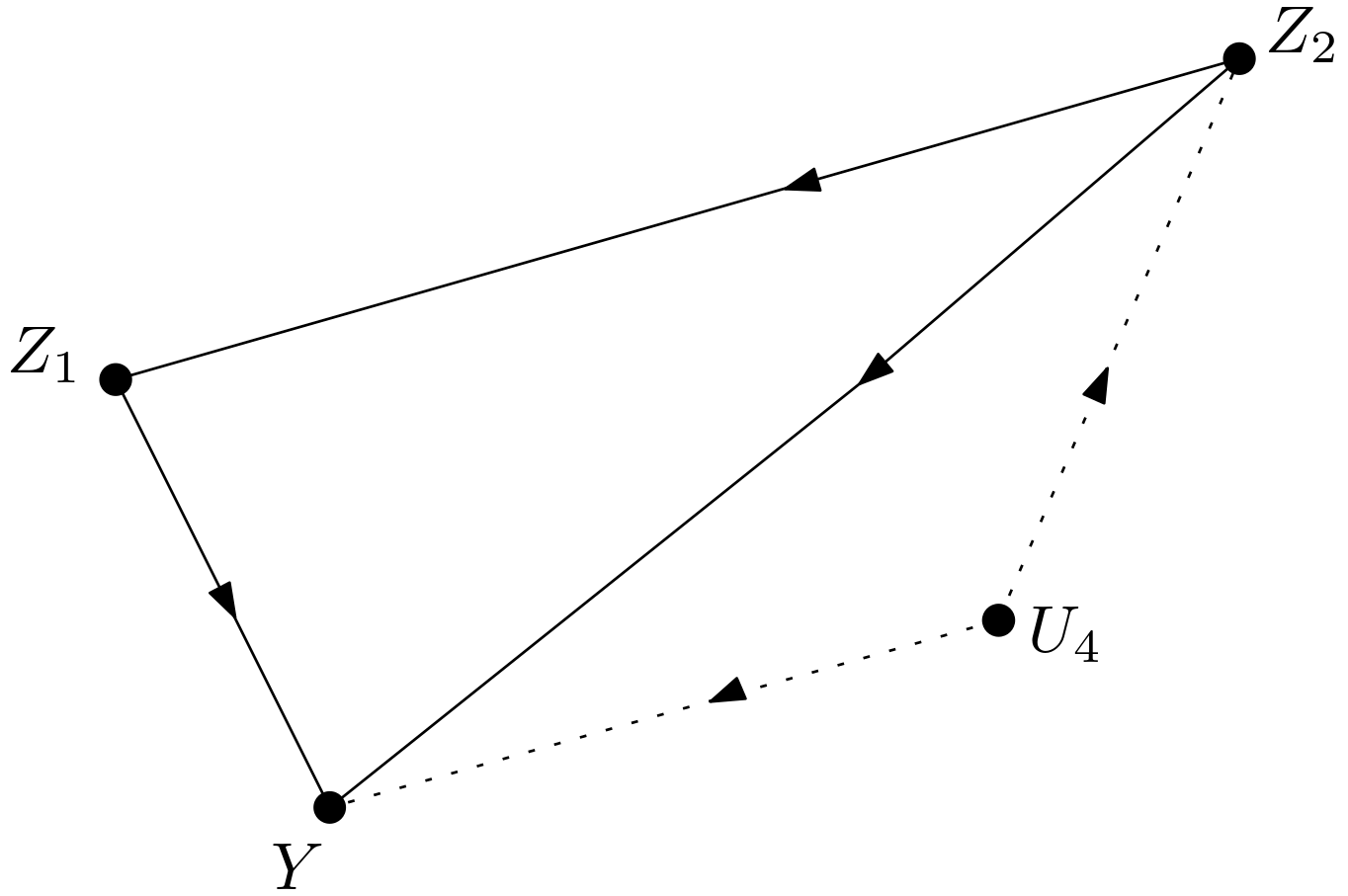
Let it be assumed that the dependencies were similar. Then, $p\left(y|do\left(z_{1}\right)\right)$ could be calculated in the $G$. $p\left(y|do\left(x\right)\right)$ should be written in a form which opens a way to incorporating the intervention of $Z_{1}$ on $Y$ into the calculation. The following expansion can be used to reach such a form: \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}p\left(y,z_{1}|do\left(x\right)\right)=\sum_{z_{1}}\frac{p\left(y,z_{1}|do\left(x\right)\right)}{p\left(z_{1}|do\left(x\right)\right)}p\left(z_{1}|do\left(x\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}p\left(y|z_{1}, do\left(x\right)\right)p\left(z_{1}|do\left(x\right)\right) \label{expansion_two} \end{equation} The expansion in the line above contains $p\left(y|z_{1}, do\left(x\right)\right)$. $p\left(y|z_{1}, do\left(x\right)\right)$ should be transformed to $p\left(y|do\left(z_{1}\right)\right)$. So, first of all, is it possible to replace the intervention on $X$ with observing $X$? Is $p\left(y|z_{1}, do\left(x\right)\right)$ equal to $p\left(y|z_{1}, x\right)$? This equality is possible if $Y$ and $X$ are conditionally d-separated given $Z_{1}$ in the graph $G_{\underline{X}}$. If $G_{\underline{X}}$ in the Figure 6 is examined, it can be detected that this conditional d-separation is impossible due to the following unblocked paths in $G_{\underline{X}}$: \begin{equation} \begin{array}{l} 1) \, X \leftarrow U_{1} \rightarrow Y \newline 2) \, X \leftarrow U_{2} \rightarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \newline 3) \, X \leftarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \newline 4) \, X \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y \newline 5) \, X \leftarrow U_{3} \rightarrow Z_{3} \rightarrow Y \end{array} \label{inter_obs_rep_unblocked_paths1} \end{equation} Can the equality be made possible by conditioning on a variable? No, because $U_{1}$ in the first unblocked path $X \leftarrow U_{1} \rightarrow Y$ is unobserved and cannot be conditioned on for blocking the path. As a result, $p\left(y|z_{1}, do\left(x\right)\right)$ cannot be written as $p\left(y|z_{1}, x\right)$.
Another choice is to remove the intervention on $X$. Is $p\left(y|z_{1}, do\left(x\right)\right)$ equal to $p\left(y|z_{1}\right)$? The removal of the intervention on $X$ is achievable if $Y$ and $X$ are conditionally d-separated given $Z_{1}$ in the graph $G_{\overline{X\left(Z_{1}\right)}}$. $X\left(Z_{1}\right)$ is the $X$ nodes which are not ancestors of $Z_{1}$ in $G$. As can be seen from the DAG in the Figure 2, $X$ is an ancestor of $Z_{1}$. Hence, $G_{\overline{X\left(Z_{1}\right)}}$ is actually $G$. In $G$, $Y$ and $X$ cannot be conditionally d-separated given $Z_{1}$ due to the same unblocked paths as the ones in the equation (\ref{inter_obs_rep_unblocked_paths1}). Can the equality be made possible by conditioning on a variable? No, because $U_{1}$ in the first unblocked path $X \leftarrow U_{1} \rightarrow Y$ is unobserved and cannot be conditioned on for blocking the path. As a result, $p\left(y|z_{1}, do\left(x\right)\right)$ cannot be written as $p\left(y|z_{1}\right)$.
Can the observation for $Z_{1}$ be replaced with the intervention on $Z_{1}$ and can this replacement be used as a starting point to deal with the intervention on $X$? For $p\left(y|z_{1}, do\left(x\right)\right)$ to be equal to $p\left(y|do\left(z_{1}\right), do\left(x\right)\right)$, $Y$ and $Z_{1}$ must be conditionally d-separated given $X$ in the graph $G_{\overline{X}\underline{Z_{1}}}$. In the Figure 12, it is clear that this conditional d-separation is impossible due to the following unblocked paths between $Y$ and $Z_{1}$: \begin{equation} \begin{array}{l} 1) \, Z_{1} \leftarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \newline 2) \, Z_{1} \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y \end{array} \end{equation} Can the equality be made possible by conditioning on a variable? Yes, conditioning on $Z_{2}$ blocks all the paths and makes $Y$ and $Z_{1}$ conditionally d-separated given $X$ and $Z_{2}$ in the graph $G_{\overline{X}\underline{Z_{1}}}$. That is, the following equation is valid: \begin{equation} p\left(y|z_{1}, z_{2}, do\left(x\right)\right) = p\left(y|do\left(z_{1}\right), z_{2}, do\left(x\right)\right) \end{equation}
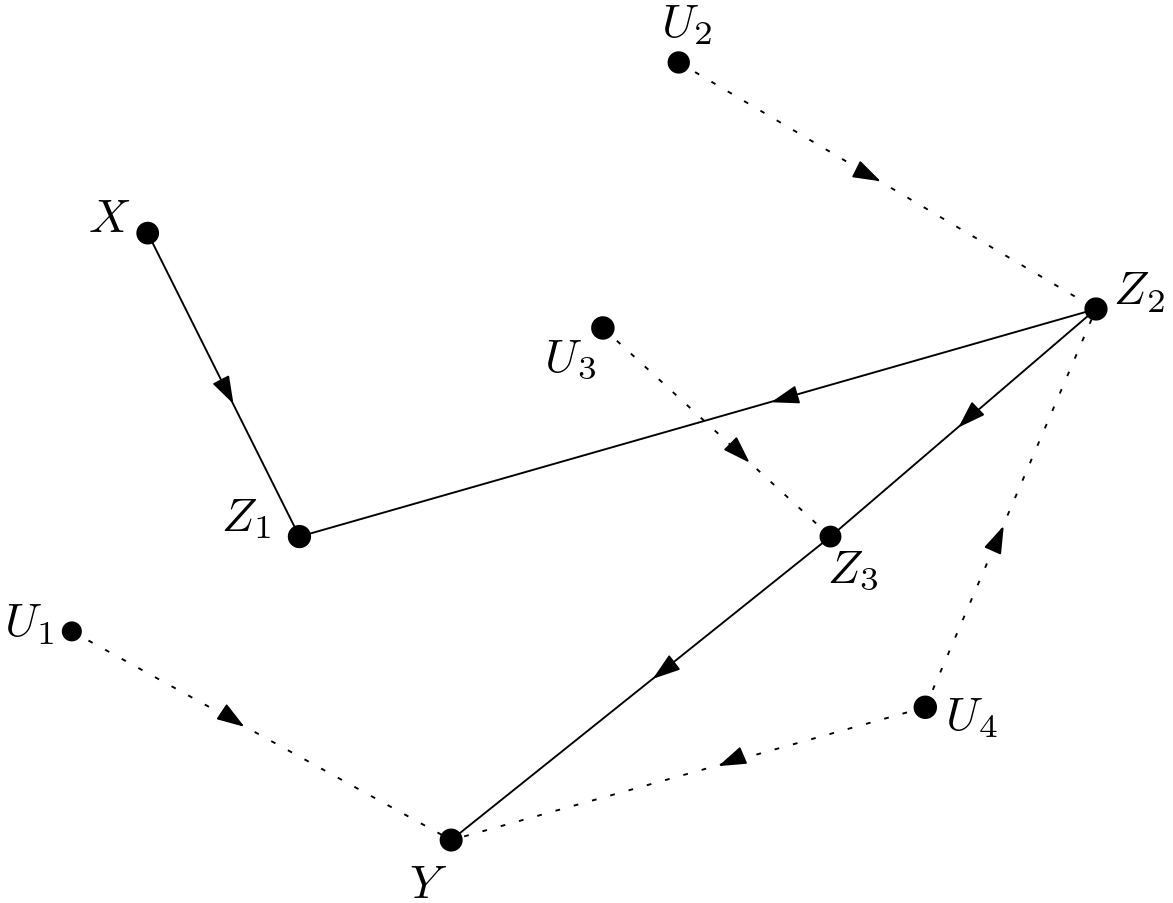
Can the intervention on $X$ be eliminated or replaced with observing $X$ in $p\left(y|do\left(z_{1}\right), z_{2}, do\left(x\right)\right)$? Let it first be examined if the intervention on $X$ can be replaced with observing $X$? This is possible if $Y$ and $X$ are conditionally d-separated given $Z_{1}$ and $Z_{2}$ in $G_{\underline{X}\overline{Z_{1}}}$. $G_{\underline{X}\overline{Z_{1}}}$ is shown in the Figure 13. Due to the unblocked paths $X \leftarrow U_{1} \rightarrow Y$ and $X \leftarrow U_{3} \rightarrow Z_{3} \rightarrow Y$, $Y$ and $X$ cannot be conditionally d-separated given $Z_{1}$ and $Z_{2}$ in $G_{\underline{X}\overline{Z_{1}}}$. The path $X \leftarrow U_{1} \rightarrow Y$ can never be blocked due to the unobserved variable $U_{1}$. Hence, $p\left(y|do\left(z_{1}\right), z_{2}, do\left(x\right)\right)$ cannot be written as $p\left(y|do\left(z_{1}\right), z_{2}, x\right)$.
Is it achievable to eliminate the intervention on $X$? Is $p\left(y|do\left(z_{1}\right), z_{2}, do\left(x\right)\right)$ equal to $p\left(y|do\left(z_{1}\right), z_{2}\right)$? The elimination of the intervention can be made if $Y$ and $X$ are conditionally d-separated given $Z_{1}$ and $Z_{2}$ in the graph $G_{\overline{X\left(Z_{2}\right)} \, \overline{Z_{1}}}$. $\overline{X\left(Z_{2}\right)}$ represents $X$ which are not ancestors of $Z_{2}$ in $G_{\overline{Z_{1}}}$. As can be seen from the Figure 13 which is infact also $G_{\overline{Z_{1}}}$, $X$ is not an ancestor of $Z_{2}$ in $G_{\overline{Z_{1}}}$. Therefore, $G_{\overline{X\left(Z_{2}\right)} \, \overline{Z_{1}}}$ is equal to $G_{\overline{X} \, \overline{Z_{1}}}$.
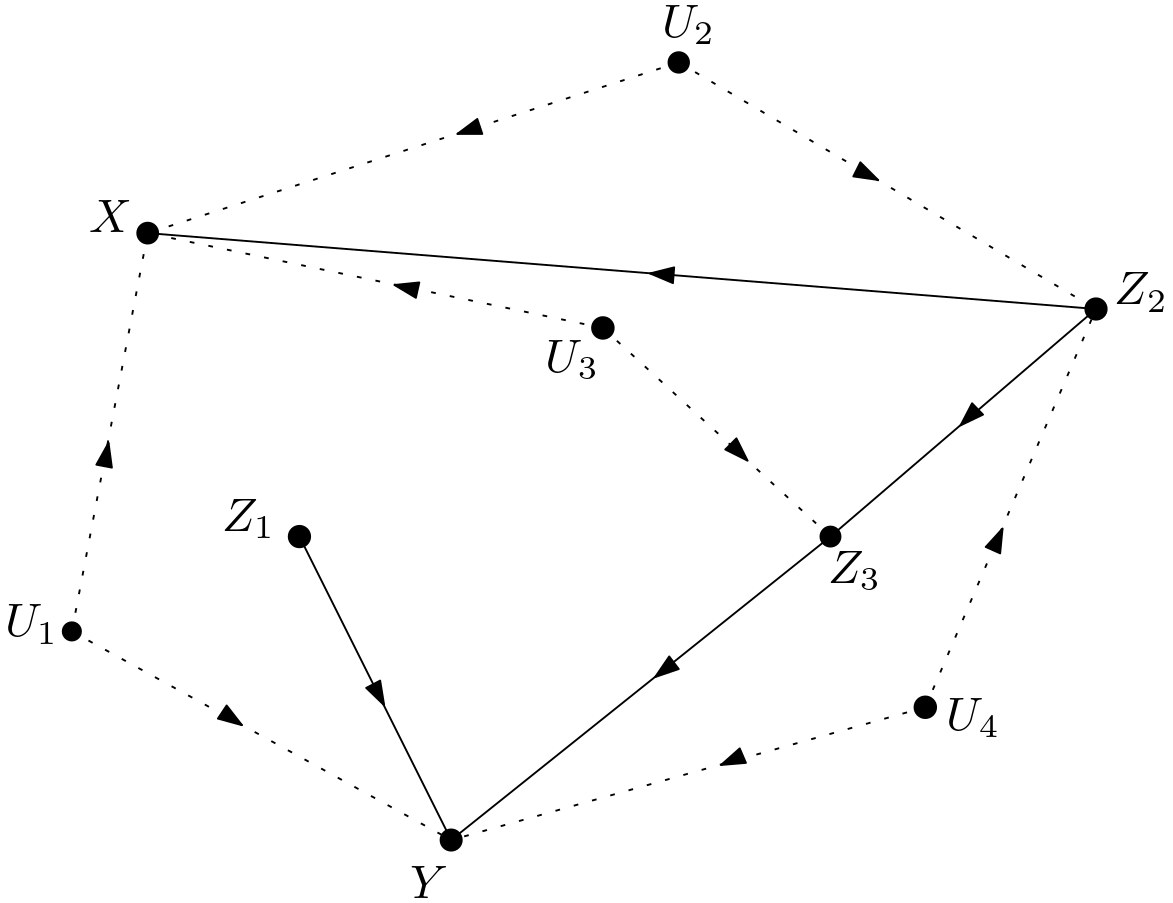
In the Figure 14, the graph $G_{\overline{X} \, \overline{Z_{1}}}$ is displayed. It can be seen from the graph that $Y$ and $X$ are conditionally d-separated given $Z_{1}$ and $Z_{2}$. Therefore: \begin{equation} p\left(y|do\left(z_{1}\right), z_{2}, do\left(x\right)\right) = p\left(y|do\left(z_{1}\right), z_{2}\right) \end{equation}
So, the following chain of equalities has been proven: \begin{equation} p\left(y|z_{1}, z_{2}, do\left(x\right)\right)=p\left(y|do\left(z_{1}\right), z_{2}, do\left(x\right)\right)=p\left(y|do\left(z_{1}\right), z_{2}\right) \label{chainOfEqualities} \end{equation} Then, it is time to incorporate $Z_{2}$ into the expansion in the equation (\ref{expansion_two}) so that the chain of equalities can be used. This incorporation can be done either using \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}\left(\sum_{z_{2}}p\left(y, z_{2}|z_{1}, do\left(x\right)\right)\right)p\left(z_{1}|do\left(x\right)\right) \label{z1z2expansion1} \end{equation} or using \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}\sum_{z_{2}}p\left(y,z_{1}, z_{2}|do\left(x\right)\right) \label{z1z2expansion2} \end{equation} In the first way of incorporation given in the equation (\ref{z1z2expansion1}), the result is \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}\left(\sum_{z_{2}}p\left(y | z_{1}, z_{2}, do\left(x\right)\right)p\left(z_{2}|do\left(x\right)\right)\right)p\left(z_{1}|do\left(x\right)\right) \end{equation} This form is not preferred since it seems lengthy, if not impossible, to calculate $p\left(z_{1}|do\left(x\right)\right)$ in $G$ in the Figure 2.
In the second way of incorporation given in the equation (\ref{z1z2expansion2}), the result is obtained as follows: \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}\sum_{z_{2}}p\left(y,z_{1}, z_{2}|do\left(x\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}\sum_{z_{2}}\frac{p\left(y,z_{1}, z_{2}|do\left(x\right)\right)}{p\left(z_{1}, z_{2}|do\left(x\right)\right)}p\left(z_{1}, z_{2}|do\left(x\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}\sum_{z_{2}}p\left(y|z_{1}, z_{2},do\left(x\right)\right)p\left(z_{1}, z_{2}|do\left(x\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}\sum_{z_{2}}p\left(y|z_{1}, z_{2},do\left(x\right)\right)\frac{p\left(z_{1}, z_{2}|do\left(x\right)\right)}{p\left(z_{2}|do\left(x\right)\right)}p\left(z_{2}|do\left(x\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}\sum_{z_{2}}p\left(y|z_{1}, z_{2},do\left(x\right)\right)p\left(z_{1}|z_{2},do\left(x\right)\right)p\left(z_{2}|do\left(x\right)\right) \end{equation} Using the equality given in the equation (\ref{chainOfEqualities}), the following final form can be obtained: \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}\sum_{z_{2}}p\left(y|do\left(z_{1}\right),z_{2}\right)p\left(z_{1}|z_{2},do\left(x\right)\right)p\left(z_{2}|do\left(x\right)\right) \label{expansion_three} \end{equation} In the above expansion, there is the term $p\left(y|do\left(z_{1}\right),z_{2}\right)$. The DAG in the Figure 11 can be used to calculate $p\left(y|do\left(z_{1}\right)\right)$. So, can this DAG help to calculate also $p\left(y|do\left(z_{1}\right),z_{2}\right)$? The intervention on $Z_{1}$ can be calculated using the probability distribution represented by the mutilated DAG in the Figure 15. Conditioning on $Z_{2}$ does not disturb the dependencies in the mutilated DAG. Hence, it is expected that $p\left(y|do\left(z_{1}\right),z_{2}\right)$ can also be calculated by the help of the DAG in the Figure 11.
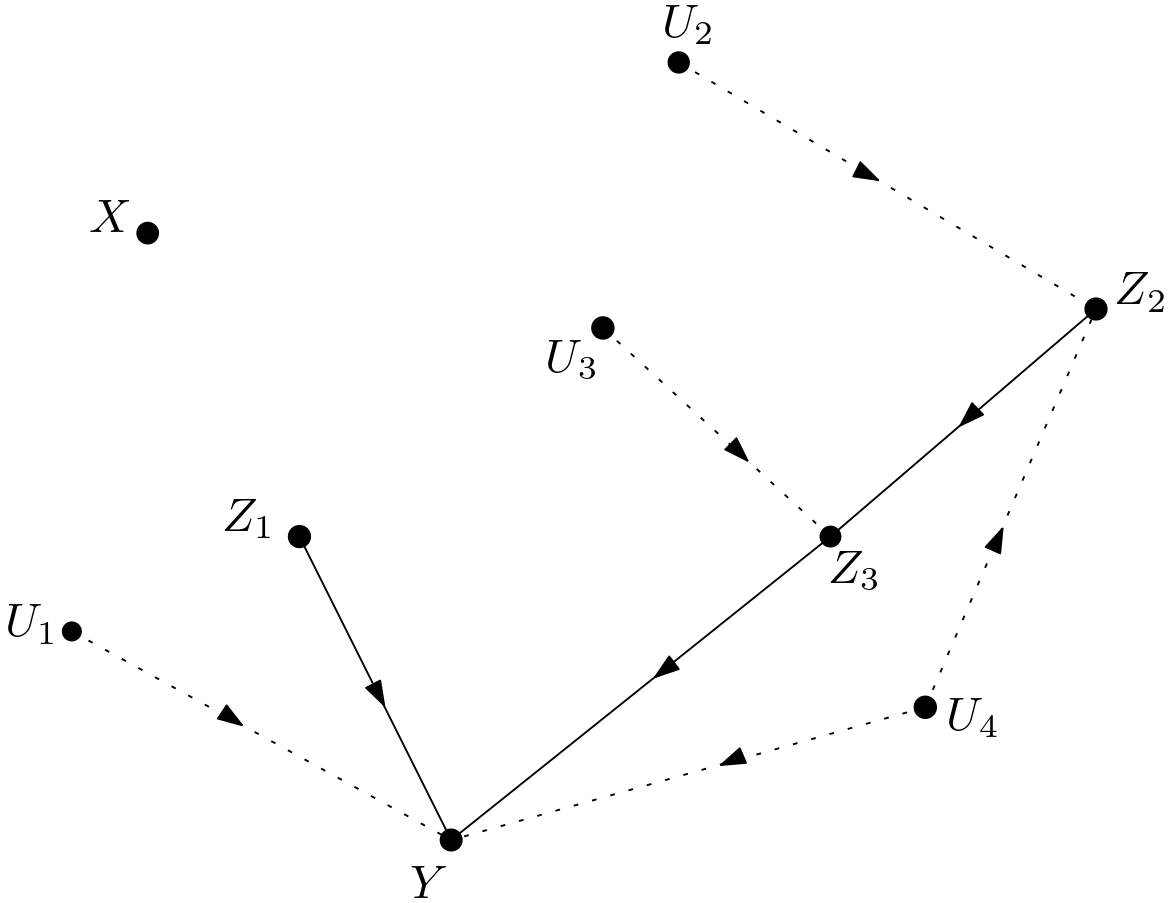
Now, it is time to examine if $p\left(y|do\left(z_{1}\right),z_{2}\right)$ can be calculated for $G$ shown in the Figure 2 using the graph in the Figure 11. Let the graph in the Figure 11 be denoted by $G_{2}$, if $G_{\overline{Z_{1}}}$ and $G_{2_{\overline{Z_{1}}}}$ share similar dependencies while $Z_{2}$ is conditioned on, then the know-how from $G_{2}$ can be utilized to calculate $p\left(y|do\left(z_{1}\right),z_{2}\right)$ in the DAG. The graph $G_{\overline{Z_{1}}}$ is shown in the Figure 16 and the graph $G_{2_{\overline{Z_{1}}}}$ is shown in the Figure 15.
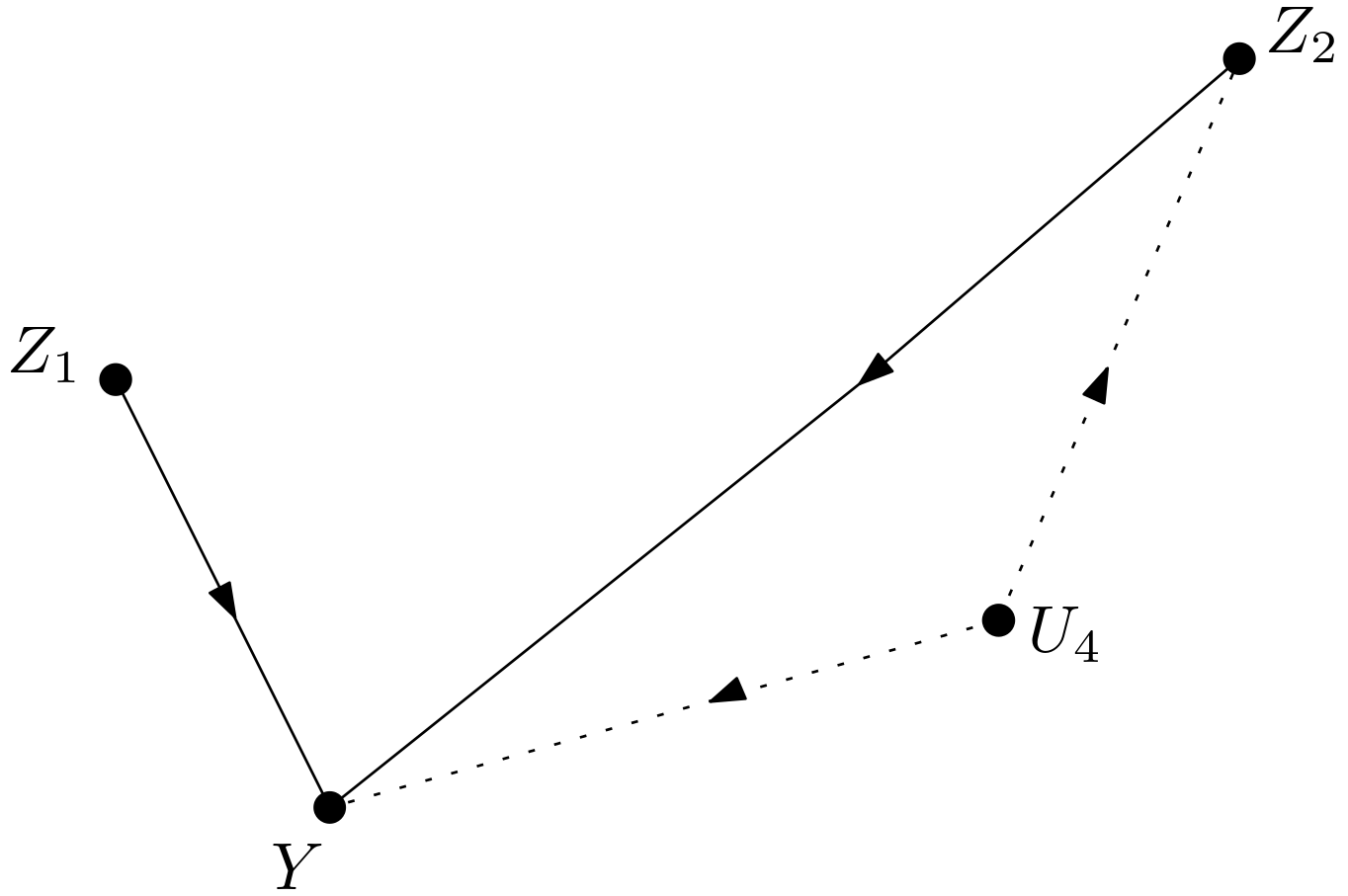
In $G_{2_{\overline{Z_{1}}}}$, there is only the path $Z_{1} \rightarrow Y$ between $Z_{1}$ and $Y$. This path is unblocked. $Z_{1} \rightarrow Y$ is also the only path between $Z_{1}$ and $Y$ in $G_{\overline{Z_{1}}}$. This path is also unblocked. Therefore, $G_{2_{\overline{Z_{1}}}}$ and $G_{\overline{Z_{1}}}$ share similar dependencies between $Y$ and $Z_{1}$.
In $G_{2_{\overline{Z_{1}}}}$, the paths between $Z_{1}$ and $Z_{2}$ are as follows: \begin{equation} \begin{array}{l} 1) \, Z_{1} \rightarrow Y \leftarrow Z_{2} \newline 2) \, Z_{1} \rightarrow Y \leftarrow U_{4} \rightarrow Z_{2} \end{array} \end{equation} Both of the paths above are blocked. In $G_{\overline{Z_{1}}}$, the paths between $Z_{1}$ and $Z_{2}$ are as follows: \begin{equation} \begin{array}{l} 1) \, Z_{1} \rightarrow Y \leftarrow U_{1} \rightarrow X \leftarrow U_{2} \rightarrow Z_{2} \newline 2) \, Z_{1} \rightarrow Y \leftarrow U_{1} \rightarrow X \leftarrow Z_{2} \newline 3) \, Z_{1} \rightarrow Y \leftarrow U_{1} \rightarrow X \leftarrow U_{3} \rightarrow Z_{3} \leftarrow Z_{2} \newline 4) \, Z_{1} \rightarrow Y \leftarrow Z_{3} \leftarrow U_{3} \rightarrow X \leftarrow U_{2} \rightarrow Z_{2} \newline 5) \, Z_{1} \rightarrow Y \leftarrow Z_{3} \leftarrow U_{3} \rightarrow X \leftarrow Z_{2} \newline 6) \, Z_{1} \rightarrow Y \leftarrow Z_{3} \leftarrow Z_{2} \newline 7) \, Z_{1} \rightarrow Y \leftarrow U_{4} \rightarrow Z_{2} \end{array} \end{equation} All the paths listed in the equation above are blocked. Hence, $G_{2_{\overline{Z_{1}}}}$ and $G_{\overline{Z_{1}}}$ share similar dependencies between $Z_{1}$ and $Z_{2}$.
In $G_{2_{\overline{Z_{1}}}}$, the paths between $Y$ and $Z_{2}$ are as follows: \begin{equation} \begin{array}{l} 1) \, Y \leftarrow Z_{2} \newline 2) \, Y \leftarrow U_{4} \rightarrow Z_{2} \end{array} \end{equation} Both of the paths above are unblocked. In $G_{\overline{Z_{1}}}$, the paths between $Y$ and $Z_{2}$ are as follows: \begin{equation} \begin{array}{l} 1) \, Y \leftarrow U_{1} \rightarrow X \leftarrow U_{2} \rightarrow Z_{2} \newline 2) \, Y \leftarrow U_{1} \rightarrow X \leftarrow Z_{2} \newline 3) \, Y \leftarrow U_{1} \rightarrow X \leftarrow U_{3} \rightarrow Z_{3} \leftarrow Z_{2} \newline 4) \, Y \leftarrow Z_{3} \leftarrow U_{3} \rightarrow X \leftarrow U_{2} \rightarrow Z_{2} \newline 5) \, Y \leftarrow Z_{3} \leftarrow U_{3} \rightarrow X \leftarrow Z_{2} \newline 6) \, Y \leftarrow Z_{3} \leftarrow Z_{2} \newline 7) \, Y \leftarrow U_{4} \rightarrow Z_{2} \end{array} \end{equation} The first five paths listed above are all blocked. The sixth and the seventh ones are unblocked and the same as the ones in $G_{2_{\overline{Z_{1}}}}$. Therefore, $G_{2_{\overline{Z_{1}}}}$ and $G_{\overline{Z_{1}}}$ share similar dependencies between $Y$ and $Z_{2}$.
| As a result, $G_{2_{\overline{Z_{1}}}}$ and $G_{\overline{Z_{1}}}$ share similar dependencies and the know-how from $G_{2}$ can be used to calculate $p\left(y | do\left(z_{1}\right),z_{2}\right)$ in $G$. |
The term $p\left(z_{1}|z_{2}, do\left(x\right)\right)$ in the equation (\ref{expansion_three}) should be examined if it can be calculated using G. Can the intervention on $X$ be replaced with observing $X$? Can $p\left(z_{1}|z_{2}, do\left(x\right)\right)$ be written as $p\left(z_{1}|z_{2}, x\right)$? This is possible if $Z_{1}$ and $X$ are conditionally d-separated given $X$ in the graph $G_{\underline{X}}$. $G_{\underline{X}}$ is shown in the Figure 6. The paths between $Z_{1}$ and $X$ can be written as follows: \begin{equation} \begin{array}{ll} 1) \, Z_{1} \rightarrow Y \leftarrow U_{1} \rightarrow X & 8) \, Z_{1} \leftarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \leftarrow U_{1} \rightarrow X \newline 2) \, Z_{1} \rightarrow Y \leftarrow Z_{3} \leftarrow U_{3} \rightarrow X & 9) \, Z_{1} \leftarrow Z_{2} \rightarrow Z_{3} \leftarrow U_{3} \rightarrow X \newline 3) \, Z_{1} \rightarrow Y \leftarrow Z_{3} \leftarrow Z_{2} \rightarrow X & 10) \, Z_{1} \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y \leftarrow U_{1} \rightarrow X \newline 4) \, Z_{1} \rightarrow Y \leftarrow Z_{3} \leftarrow Z_{2} \leftarrow U_{2} \rightarrow X & 11) \, Z_{1} \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y \leftarrow Z_{3} \leftarrow U_{3} \rightarrow X \newline 5) \, Z_{1} \rightarrow Y \leftarrow U_{4} \rightarrow Z_{2} \rightarrow X & 12) \, Z_{1} \leftarrow Z_{2} \leftarrow U_{2} \rightarrow X \newline 6) \, Z_{1} \rightarrow Y \leftarrow U_{4} \rightarrow Z_{2} \leftarrow U_{2} \rightarrow X & 13) \, Z_{1} \leftarrow Z_{2} \rightarrow X \newline 7) \, Z_{1} \rightarrow Y \leftarrow U_{4} \rightarrow Z_{2} \rightarrow Z_{3} \leftarrow U_{3} \rightarrow X \end{array} \end{equation} The first path is blocked due to the collider $Z_{1} \rightarrow Y \leftarrow U_{1}$. The second path is blocked due to the collider $Z_{1} \rightarrow Y \leftarrow Z_{3}$. The third and fourth paths are blocked due to the collider $Z_{1} \rightarrow Y \leftarrow Z_{3}$ or conditioning on $Z_{2}$. The fifth path is blocked due to the collider $Z_{1} \rightarrow Y \leftarrow U_{4}$ or conditioning on $Z_{2}$. The sixth path is blocked due to the collider $Z_{1} \rightarrow Y \leftarrow U_{4}$. The seventh path is blocked due to the collider $Z_{1} \rightarrow Y \leftarrow U_{4}$ or conditioning on $Z_{2}$ or the collider $Z_{2} \rightarrow Z_{3} \leftarrow U_{3}$. The eighth path is blocked due to conditioning on $Z_{2}$ or the collider $Z_{3} \rightarrow Y \leftarrow U_{1}$. The ninth path is blocked due to conditioning on $Z_{2}$ or the collider $Z_{2} \rightarrow Z_{3} \leftarrow U_{3}$. The tenth path is blocked due to conditioning on $Z_{2}$ or the collider $U_{4} \rightarrow Y \leftarrow U_{1}$. The eleventh path is blocked due to conditioning on $Z_{2}$ or the collider $U_{4} \rightarrow Y \leftarrow Z_{3}$. The twelfth and the thirteenth paths are blocked due to conditioning on $Z_{2}$. Therefore, $Z_{1}$ and $X$ are conditionally d-separated given $Z_{2}$ in the graph $G_{\underline{X}}$ and the following equality is valid: \begin{equation} p\left(z_{1}|z_{2}, do\left(x\right)\right)=p\left(z_{1}|z_{2},x\right) \end{equation} After overcoming $p\left(z_{1}|z_{2}, do\left(x\right)\right)$ in the equation (\ref{expansion_three}), it is the turn of $p\left(z_{2}|do\left(x\right)\right)$. Can the intervention on $X$ be removed? Can $p\left(z_{2}|do\left(x\right)\right)$ be written as $p\left(z_{2}\right)$? This is possible if $Z_{2}$ and $X$ are d-separated in the graph $G_{\overline{X}}$. In the Figure 7, $G_{\overline{X}}$ is drawn. The paths between $Z_{2}$ and $X$ are as follows: \begin{equation} \begin{array}{l} 1) \, X \rightarrow Z_{1} \leftarrow Z_{2} \newline 2) \, X \rightarrow Z_{1} \rightarrow Y \leftarrow Z_{3} \leftarrow Z_{2} \newline 3) \, X \rightarrow Z_{1} \rightarrow Y \leftarrow U_{4} \rightarrow Z_{2} \end{array} \end{equation} The first path is blocked due to its collider structure. The second path is blocked due to the collider $Z_{1} \rightarrow Y \leftarrow Z_{3}$. The third path is blocked due to the collider $Z_{1} \rightarrow Y \leftarrow U_{4}$. Hence, $Z_{2}$ and $X$ are d-separated in the graph $G_{\overline{X}}$, which means that $p\left(z_{2}|do\left(x\right)\right)$ can be written as $p\left(z_{2}\right)$.
Resultantly, the expansion in the equation (\ref{expansion_three}) can be expressed as follows: \begin{equation} p\left(y|do\left(x\right)\right)=\sum_{z_{1}}\sum_{z_{2}}p\left(y|do\left(z_{1}\right),z_{2}\right)p\left(z_{1}|z_{2},x\right)p\left(z_{2}\right) \label{expansion_four} \end{equation} It has been proven that $p\left(y|do\left(z_{1}\right),z_{2}\right)$ can be calculated using only the graph in the Figure 11. Hence, using the know-how from the graph in the Figure 11 and the expansion in the equation (\ref{expansion_four}), $p\left(y|do\left(x\right)\right)$ in $G$ can be calculated.
It is the turn of the graph in the Figure 3.8 (d) of [1]. It is drawn in the Figure 17. The subgraph of $G$ matching to this graph is indicated in red in the Figure 18. If the dependencies in the mutilated form of this graph and that of $G$ are similar, then the know-how from the graph in the Figure 19 can be used to calculate the causal effect of $X$ on $Z_{1}$ in $G$. Let it be assumed that the dependencies were similar. $p(y|do(x))$ should be written in a form which opens a way to incorporating $p\left(z_{1}|do\left(x\right)\right)$ into the calculation. The following expansion can be used to reach such a form: \begin{equation} p(y|do(x))=\sum_{z_{1}}p\left(y,z_{1}|do\left(x\right)\right)=\sum_{z_{1}}\frac{p\left(y,z_{1}|do\left(x\right)\right)}{p\left(z_{1}|do\left(x\right)\right)}p\left(z_{1}|do\left(x\right)\right) \Rightarrow \end{equation} \begin{equation} p(y|do(x))=\sum_{z_{1}}p\left(y|z_{1}, do\left(x\right)\right)p\left(z_{1}|do\left(x\right)\right) \label{expansion_five} \end{equation} As can be seen from the equation (\ref{expansion_five}), $p\left(z_{1}|do\left(x\right)\right)$ has been incorporated into the calculation of the causal effect of $X$ on $Y$. Is there a way to calculate $p\left(y|z_{1}, do\left(x\right)\right)$ using the know-how from the graph shown in the Figure 19? The know-how enables one to find the causal effect of $X$ on $Z_{1}$, not on $Y$. The graph displayed in the Figure 19 cannot be used to find $p\left(y|z_{1},do\left(x\right)\right)$. Hence, using only the graph in the Figure 3.8 (d) of [1], it is not possible to calculate $p\left(y, do\left(x\right)\right)$ for $G$.
Conclusion
The graphs in the Figure 3.8 (b), (c) and (d) of [1] have been examined to determine if the causal effect of $X$ on $Y$ in $G$ shown in the Figure 2 can be calculated using only one of those three graphs. It has been shown that using only the graph in (b) or only the graph in (d) cannot help solving the causal effect. However, using only the graph in (c), the causal effect can be calculated.
References
[1] Judea Pearl, Causality: Models, Reasoning and Inference, Cambridge University Press, 2009.