Introduction
First of all, this article is best viewed in Chromium and Google Chrome browsers. Some characters are not rendered correctly in Firefox. In this article, an example is to be given for the graph topology guided causal effect calculation. The graph topology guided causal effect calculation is demonstrated on the page 93 of [1]. A similar technique is to be applied to calculate the causal effect of $X$ on $Y$ for the directed acyclic graph (DAG) shown in the subfigure (g) of the Figure 3.8 on the page 92 of [1].
The DAG
The DAG to be studied for the calculation of the causal effect of $X$ on $Y$ is shown in the Figure 1.
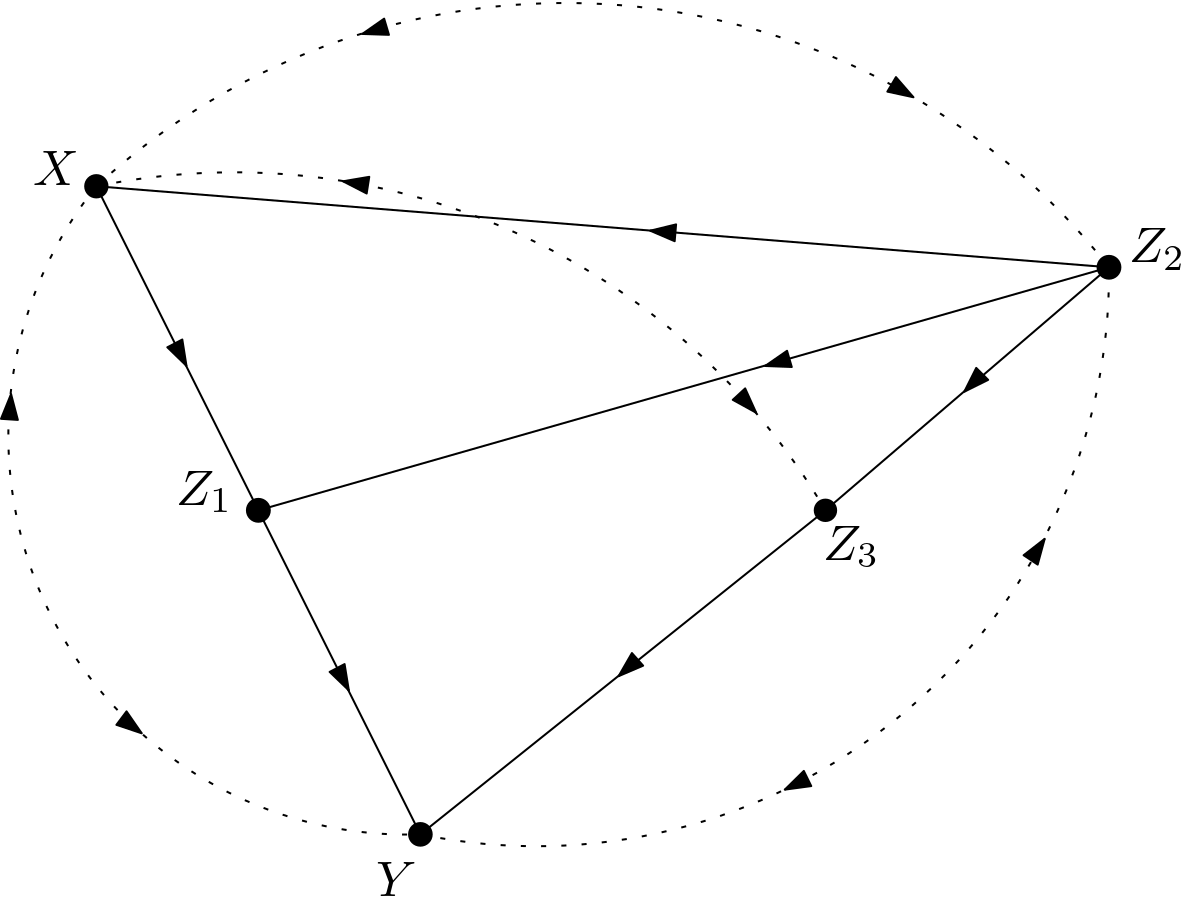
This DAG can be redrawn in the Figure 2 to make the unobserved variables explicit.
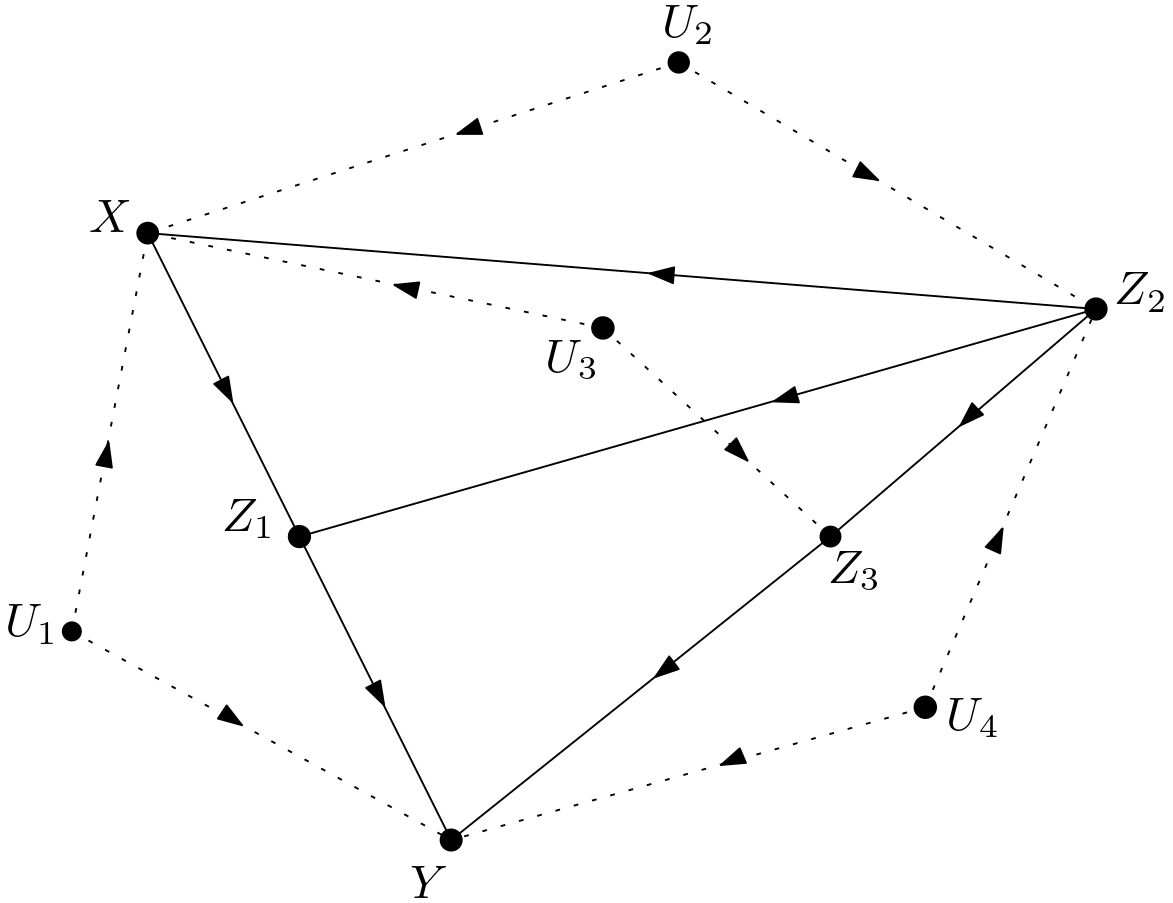
The Backdoor Criterion
First, the backdoor criterion is checked to see if it can handle the calculation of the causal effect. The backdoor path $X \leftarrow U_{1} \rightarrow Y$ cannot be blocked since $U_{1}$ is unobserved. The existance of this backdoor path which can never be blocked makes it impossible to use the adjustment formula for the calculation of the causal effect.
The Rules Of Do-calculus
The first rule is the replacement of the intervention with the related observation. Can the intervention on $X$ be replaced with an observation of $X$, i.e. \begin{equation} p\left(y|do\left(x\right)\right) \stackrel{?}{=} p\left(y|x\right) \end{equation} Provided the original DAG is denoted by $G$, if $X$ and $Y$ are d-separated in the DAG $G_{\underline{X}}$, then the replacement can be made.
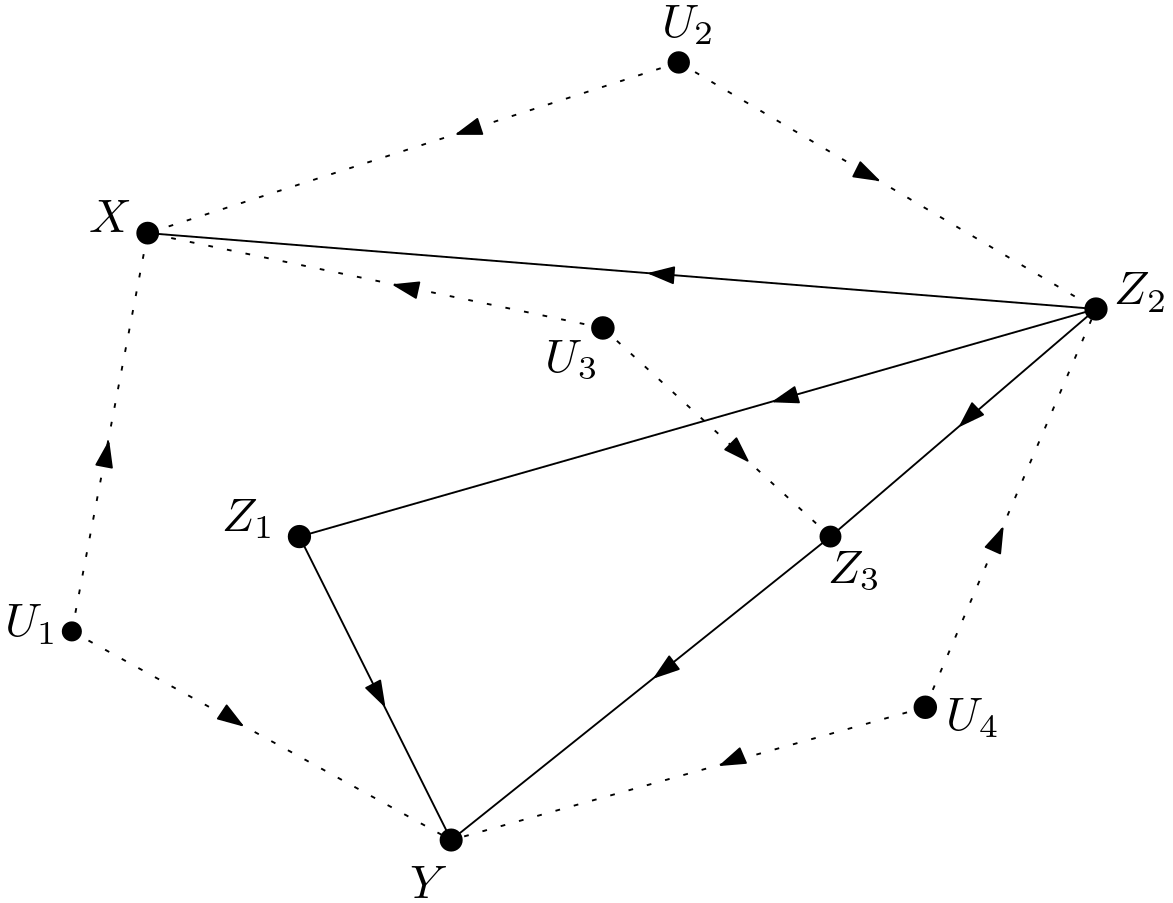
As can be seen in the Figure 3, there are the following unblocked backdoor paths between $X$ and $Y$: \begin{equation} \begin{array}{l} X \leftarrow U_{1} \rightarrow Y \newline X \leftarrow U_{2} \rightarrow Z_{2} \rightarrow Z_{1} \rightarrow Y \newline X \leftarrow U_{2} \rightarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \newline X \leftarrow U_{3} \rightarrow Z_{3} \rightarrow Y \newline X \leftarrow U_{3} \rightarrow Z_{3} \leftarrow Z_{2} \rightarrow Z_{1} \rightarrow Y \newline X \leftarrow U_{3} \rightarrow Z_{3} \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y\newline X \leftarrow Z_{2} \rightarrow Z_{1} \rightarrow Y \newline X \leftarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \newline X \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y \end{array} \end{equation} Hence, $X$ and $Y$ are not d-separated in the DAG $G_{\underline{X}}$. This implies that \begin{equation} p\left(y|do\left(x\right)\right) \neq p\left(y|x\right) \end{equation} The other choice is the removal of the intervention. Can the intervention on $X$ be removed, i.e. \begin{equation} p\left(y|do\left(x\right)\right) \stackrel{?}{=} p\left(y\right) \end{equation} This equality is possible if $X$ and $Y$ are d-separated in the DAG $G_{\overline{X}}$.
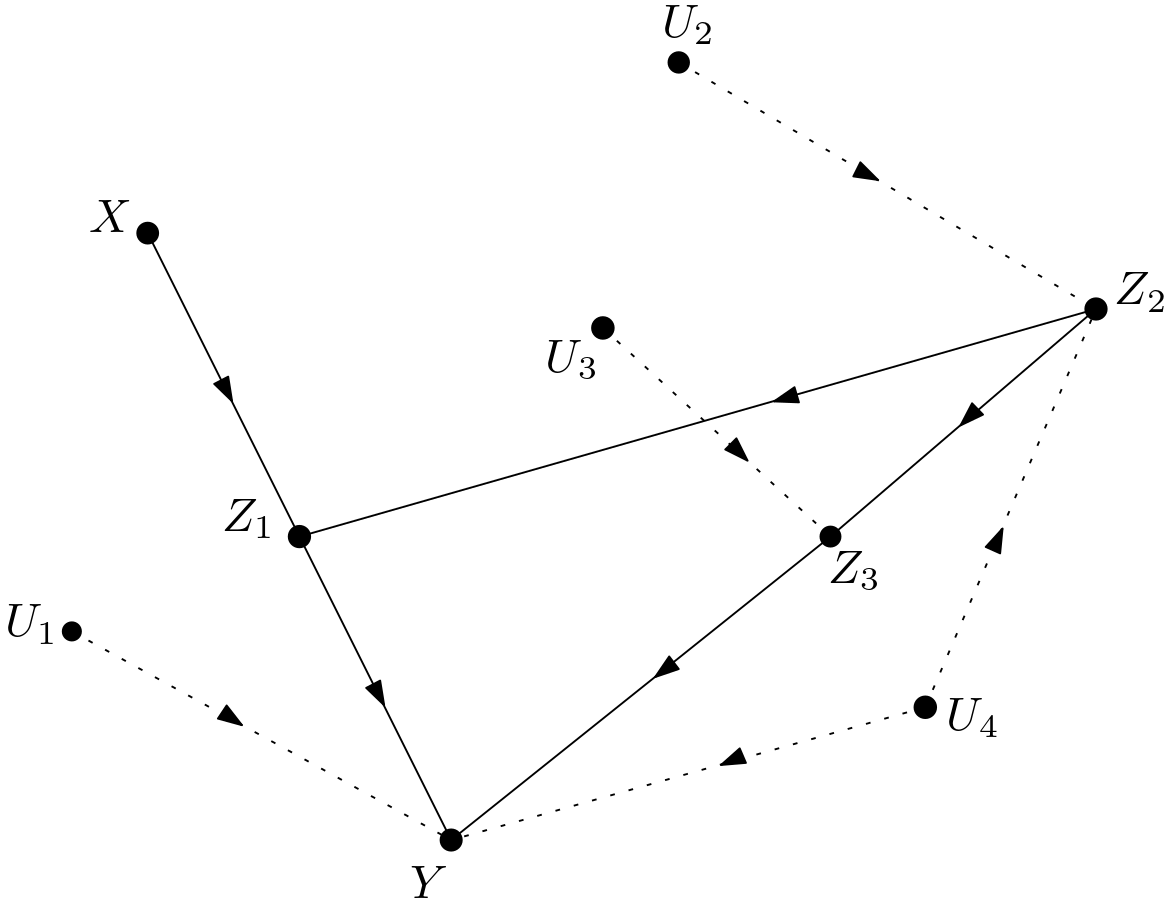
From the Figure 4, it can be detected that the path $X \rightarrow Z_{1} \rightarrow Y$ between $X$ and $Y$ is unblocked. Hence, $X$ and $Y$ are not d-separated in the DAG $G_{\overline{X}}$. This implies that \begin{equation} p\left(y|do\left(x\right)\right) \neq p\left(y\right) \end{equation} As a result, a solution for the causal effect of $X$ on $Y$ couldn’t be found by means of the simple application of the rules of the do-calculus.
Topology Guided Causal Effect Calculation
The idea behind the topology guided causal effect calculation is detecting sub-graphs of the DAG under investigation in such a way that these subgraphs identify causal effects which can be combined to obtain the target causal effect. There are such subgraphs in the DAG shown in the Figure 2. In the Figure 5, the red subgraph is an identifying DAG.
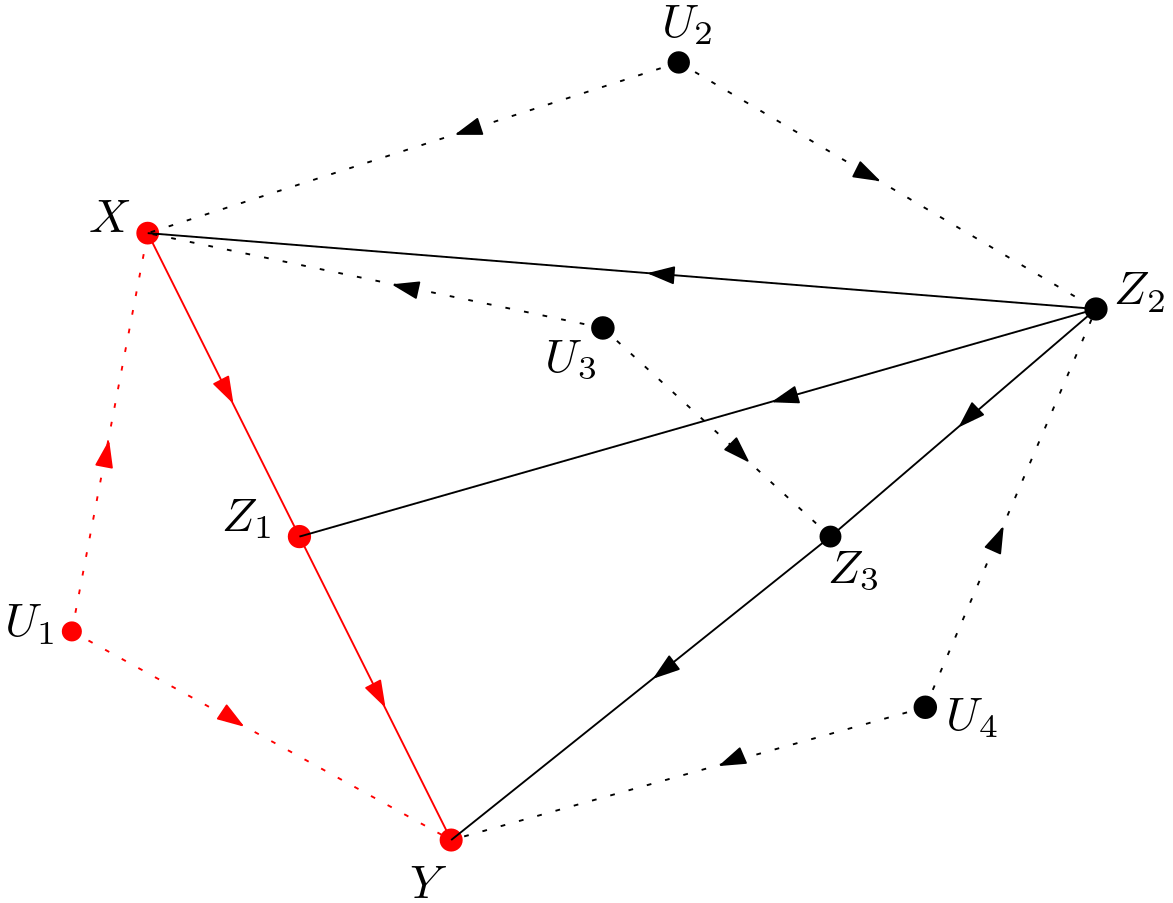
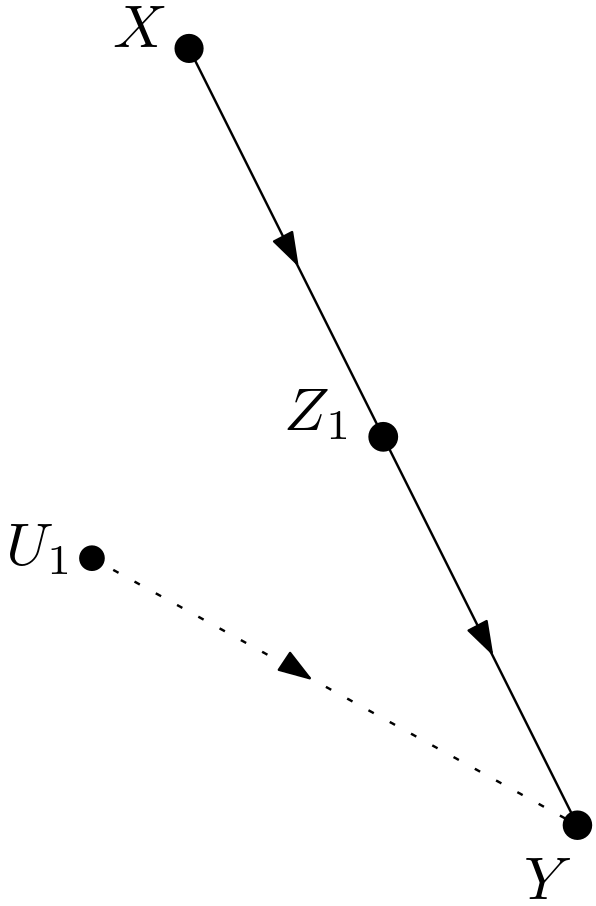
Considering that this subgraph can prospectively be used for the calculation of the causal quantity $p\left(y|do\left(x\right)\right)$, let the causal quantity be expanded as in the following total probability form: \begin{equation} p\left(y|do\left(x\right)\right) = \sum_{z_{1}} p\left(y,z_{1}|do\left(x\right)\right) \end{equation} $p\left(y,z_{1}|do\left(x\right)\right)$ can be identified by the subgraph. In this identification, the follow-ing form of the joint distribution is used: \begin{equation} p\left(y,z_{1}|do\left(x\right)\right)=p\left(y|z_{1},do\left(x\right)\right)p\left(z_{1}|do\left(x\right)\right) \end{equation} But, can this identification be used in the DAG of Figure 2? This identification can be used in the original DAG only if the dependencies in the manipulated subgraph are similar to those in the manipulated original DAG. The manipulated subgraph is shown in the Figure 6.
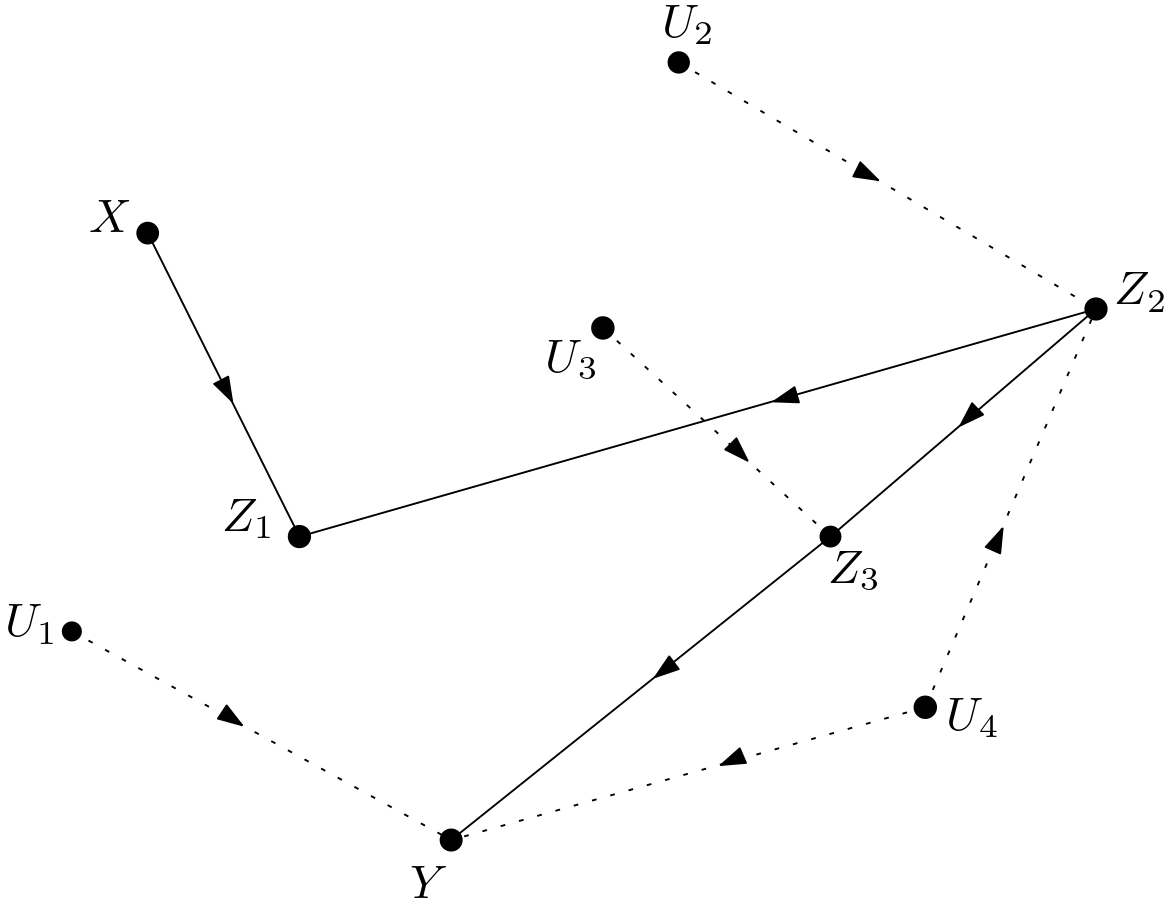
The manipulated original DAG is shown in the Figure 7.

In the manipulated subgraph, there is only one path from $X$ to $Z_{1}$ as $X \rightarrow Z_{1}$. In the manipulated original DAG, there is also only one path from $X$ to $Z_{1}$ as $X \rightarrow Z_{1}$. It is obvious that the manipulated subgraph and the manipulated original DAG share similar dependencies for $p\left(z_{1}|do\left(x\right)\right)$. As to $p\left(y|z_{1},do\left(x\right)\right)$, in the Figure 6, there is only one path from $X$ to $Y$ as $X \rightarrow Z_{1} \rightarrow Y$. In the Figure 7, there are additional two paths from $X$ to $Y$. They are $X\rightarrow Z_{1} \leftarrow Z_{2} \rightarrow Z_{3} \rightarrow Y$ and $X\rightarrow Z_{1} \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y$. These paths are unblocked to conditioning on $Z_{1}$. The manipulated subgraph and the manipulated original graph do not share similar dependencies for $p\left(y|z_{1},do\left(x\right)\right)$. After the examination of dependency similarity, it can be stated that the identification of $p\left(y, z_{1}| do\left(x\right)\right)$ in the subgraph cannot be used in the original DAG. The paths $X\rightarrow Z_{1} \leftarrow Z_{2} \rightarrow Z_{3} \rightarrow Y$ and $X\rightarrow Z_{1} \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y$ can be blocked by conditioning on $Z_{2}$. In order to attain conditioning on $Z_{2}$, it is a good idea to start with the total probability rule over the two variables $Z_{1}$ and $Z_{2}$: \begin{equation} p\left(y|do\left(x\right)\right) = \sum_{z_{1}} \sum_{z_{2}} p\left(y,z_{1}, z_{2}|do\left(x\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(y|do\left(x\right)\right) = \sum_{z_{1}} \sum_{z_{2}} p\left(y,z_{1}|z_{2},do\left(x\right)\right)p\left(z_{2}|do\left(x\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(y|do\left(x\right)\right) = \sum_{z_{1}} \sum_{z_{2}} p\left(y|z_{1},z_{2},do\left(x\right)\right) p\left(z_{1}|z_{2},do\left(x\right)\right) p\left(z_{2}|do\left(x\right)\right) \label{double_total_sum} \end{equation} There is now a conditioning on $Z_{2}$ in $p\left(y|z_{1},z_{2},do\left(x\right)\right)$ as can be detected from the equation (\ref{double_total_sum}).
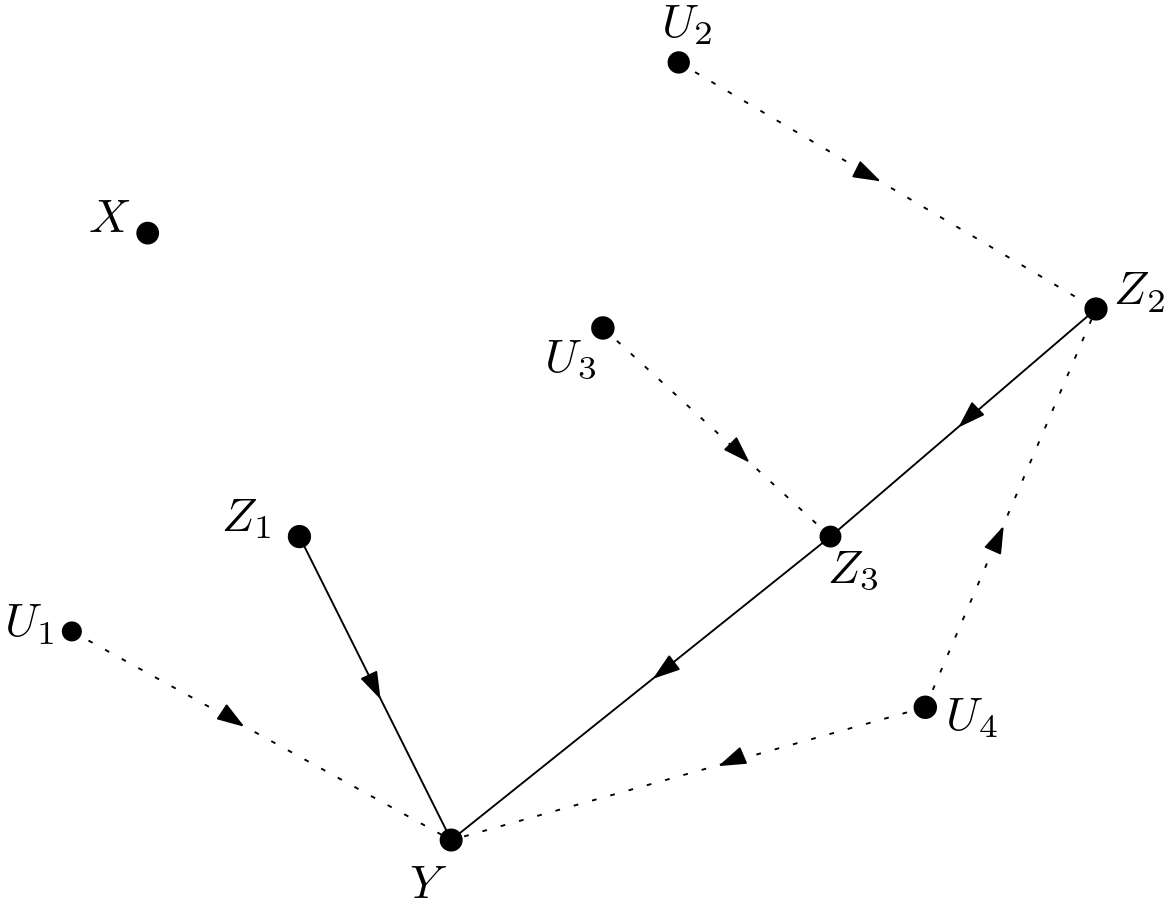
Let $p\left(z_{1}|z_{2},do\left(x\right)\right)$ be calculated first. From the Figure 2, the backdoor paths from $X$ to $Z_{1}$ can be listed as follows: \begin{equation} \begin{array}{l} 1) \, X \leftarrow U_{1} \rightarrow Y \leftarrow Z_{1} \newline 2) \, X \leftarrow U_{2} \rightarrow Z_{2} \rightarrow Z_{1} \newline 3) \, X \leftarrow U_{2} \rightarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \leftarrow Z_{1} \newline 4) \, X \leftarrow U_{2} \rightarrow Z_{2} \leftarrow U_{4} \rightarrow Y \leftarrow Z_{1} \newline 5) \, X \leftarrow U_{3} \rightarrow Z_{3} \rightarrow Y \leftarrow Z_{1} \newline 6) \, X \leftarrow U_{3} \rightarrow Z_{3} \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y \leftarrow Z_{1} \newline 7) \, X \leftarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \leftarrow Z_{1} \newline 8) \, X \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y \leftarrow Z_{1} \newline \end{array} \end{equation} The first one is blocked due to the collider $U_{1} \rightarrow Y \leftarrow Z_{1}$. The second one is blocked due to conditioning on $Z_{2}$. The third one is blocked due to conditioning on $Z_{2}$ or the collider $Z_{3} \rightarrow Y \leftarrow Z_{1}$. The fourth one is blocked due to conditioning on $Z_{2}$ or the collider $U_{4} \rightarrow Y \leftarrow Z_{1}$. The fifth one is blocked due to the collider $Z_{3} \rightarrow Y \leftarrow Z_{1}$. The sixth one is blocked due to conditioning on $Z_{2}$ or the collider $U_{4} \rightarrow Y \leftarrow Z_{1}$. The seventh one is blocked due to conditioning on $Z_{2}$ or the collider $Z_{3} \rightarrow Y \leftarrow Z_{1}$. The last one is blocked due to conditioning on $Z_{2}$ or the collider $U_{4} \rightarrow Y \leftarrow Z_{1}$. Since all the backdoor paths from $X$ to $Z_{1}$ are blocked, the following equality can safely be written: \begin{equation} p\left(z_{1}|z_{2},do\left(x\right)\right)=p\left(z_{1}|z_{2},x\right) \end{equation} Let $p\left(y|z_{1},z_{2},do\left(x\right)\right)$ be dealt with. In the calculation of this causal quantity, the know-how from the subgraph shown in red in the Figure 5 is to be utilized. Can the observation of $Z_{1}$ be replaced with the intervention on $Z_{1}$? In other words, \begin{equation} p\left(y|z_{1},z_{2},do\left(x\right)\right) \stackrel{?}{=} p\left(y|do\left(z_{1}\right),z_{2},do\left(x\right)\right) \end{equation} This is possible if $Y$ and $Z_{1}$ are conditionally d-separated given $Z_{2}$ and $X$ in $G_{\overline{X}\underline{Z_{1}}}$. $G_{\overline{X}\underline{Z_{1}}}$ is displayed in the Figure 8.
The paths $Z_{1} \leftarrow Z_{2} \rightarrow Z_{3} \rightarrow Y$ and $Z_{1} \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y$ are both blocked by conditioning on $Z_{2}$. Hence, $Y$ and $Z_{1}$ are conditionally d-separated given $Z_{2}$ and $X$ in $G_{\overline{X}\underline{Z_{1}}}$, which implies the following: \begin{equation} p\left(y|z_{1},z_{2},do\left(x\right)\right) = p\left(y|do\left(z_{1}\right),z_{2},do\left(x\right)\right) \end{equation} Can the intervention on $X$ be removed? In other words, is $p\left(y|do\left(z_{1}\right),z_{2},do\left(x\right)\right)$ equal to $p\left(y|do\left(z_{1}\right),z_{2}\right)$? This is possible if $Y$ and $X$ are conditionally d-separated given $Z_{1}$ and $Z_{2}$ in the graph $G_{\overline{Z_{1}} \, \overline{X\left(Z_{2}\right)}}$. $X\left(Z_{2}\right)$ denotes the set of $X$ nodes which are not ancestors of $Z_{2}$ in $G_{\overline{X}}$. If the Figure 4 is inspected, then it can be determined that \begin{equation} X\left(Z_{2}\right)=X \end{equation} Therefore, the graph $G_{\overline{Z_{1}} \, \overline{X}}$ is needed. It is shown in the Figure 9.
From this figure, it is clear that $Y$ and $X$ are conditionally d-separated given $Z_{1}$ and $Z_{2}$. Hence, the following equality can safely be written: \begin{equation} p\left(y|do\left(z_{1}\right),z_{2},do\left(x\right)\right)=p\left(y|do\left(z_{1}\right),z_{2}\right) \label{simplification2} \end{equation} Now, $p\left(y|do\left(z_{1}\right),z_{2}\right)$ is to be worked on. The experience from the subgraph shown in red in the Figure 5 is going to be utilized again. The intervention in $p\left(y|do\left(z_{1}\right),z_{2}\right)$ is to be replaced by an observation of $Z_{1}$. This is possible if $Y$ and $Z_{1}$ are conditionally d-separated given $Z_{2}$ in $G_{\underline{Z_{1}}}$. The graph $G_{\underline{Z_{1}}}$ is displayed in the Figure 10.
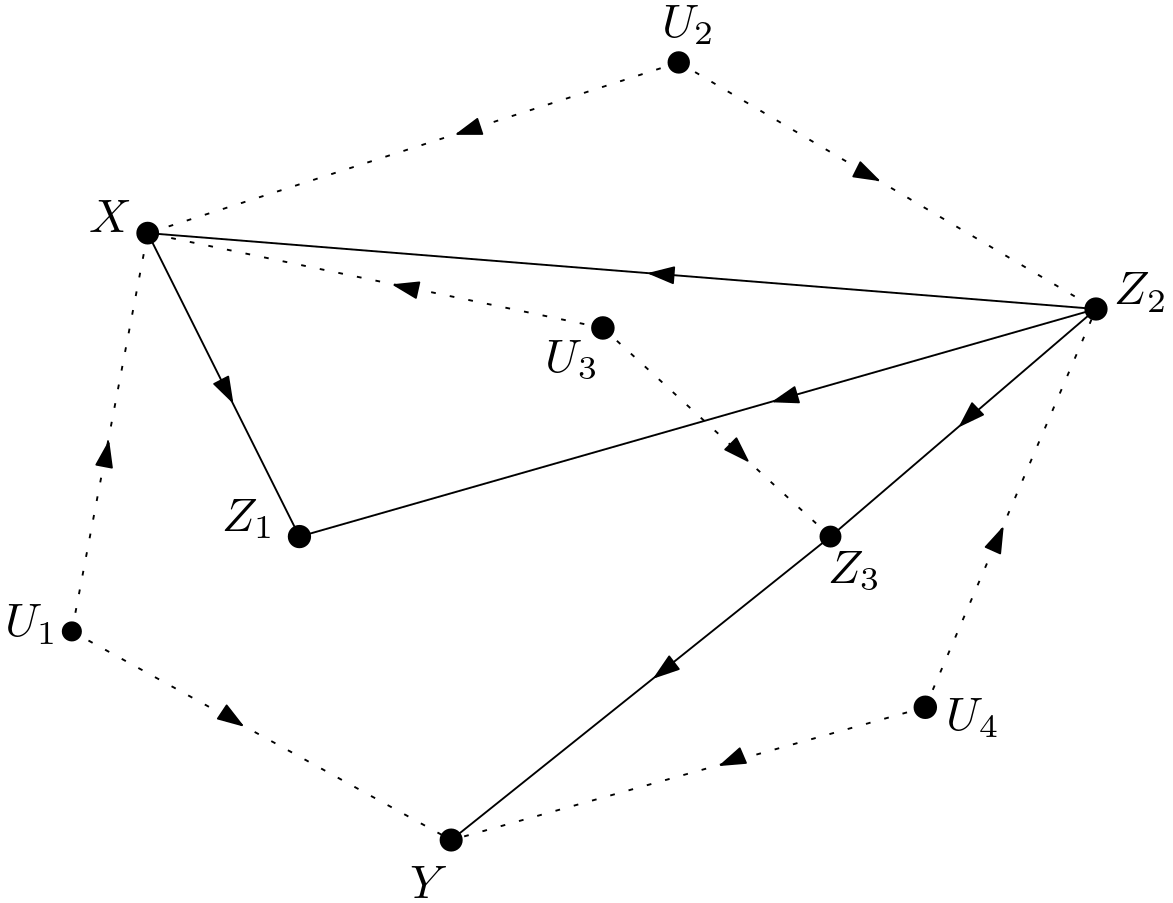
The backdoors from $Z_{1}$ to $Y$ in $G_{\underline{Z_{1}}}$ are as follows: \begin{equation} \begin{array}{l} 1) \, Z_{1} \leftarrow X \leftarrow U_{2} \rightarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \newline 2) \, Z_{1} \leftarrow X \leftarrow U_{2} \rightarrow Z_{2} \leftarrow U_{4} \rightarrow Y \newline 3) \, Z_{1} \leftarrow X \leftarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \newline 4) \, Z_{1} \leftarrow X \leftarrow U_{3} \rightarrow Z_{3} \rightarrow Y \newline 5) \, Z_{1} \leftarrow X \leftarrow U_{3} \rightarrow Z_{3} \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y \newline 6) \, Z_{1} \leftarrow X \leftarrow U_{1} \rightarrow Y \end{array} \label{backdoor_z1_y} \end{equation} Path 1 and path 3 are blocked due to conditioning on $Z_{2}$. Path 2 is unblocked due to condition-ing on $Z_{2}$. Path 4 is unblocked. Path 5 is blocked due to conditioning on $Z_{2}$ or the collider $U_{3} \rightarrow Z_{3} \leftarrow Z_{2}$. Path 6 is unblocked. Conditioning on $X$ blocks path 2, path 4 and path 6 without disturbing the states of the paths 1, 3 and 5. Hence, in order to attain conditioning on $X$, $p\left(y|do\left(z_{1}\right),z_{2}\right)$ should be written as a total probability sum over all possible values of $X$: \begin{equation} p\left(y|do\left(z_{1}\right),z_{2}\right)=\sum_{x^{\prime}} p\left(y, x^{\prime}|do\left(z_{1}\right),z_{2}\right) \Rightarrow \end{equation} \begin{equation} p\left(y|do\left(z_{1}\right),z_{2}\right)=\sum_{x^{\prime}} p\left(y|x^{\prime}, do\left(z_{1}\right),z_{2}\right)p\left(x^{\prime}| do\left(z_{1}\right),z_{2}\right) \label{total_sum_on_X} \end{equation} Let $p\left(x^{\prime}| do\left(z_{1}\right),z_{2}\right)$ be examined first. Can the intervention on $Z_{1}$ be removed? The removal is possible if $X$ and $Z_{1}$ are conditionally d-separated given $Z_{2}$ in $G_{\overline{Z_{1}\left(Z_{2}\right)}}$. $Z_{1}\left(Z_{2}\right)$ represents the set of $Z_{1}$ nodes which are not ancestors of $Z_{2}$ in $G_{\overline{Z}_{1}}$. $G_{\overline{Z}_{1}}$ is given in the Figure 11. It is evident from this figure that \begin{equation} Z_{1}\left(Z_{2}\right)=Z_{1} \Rightarrow G_{\overline{Z_{1}\left(Z_{2}\right)}}=G_{\overline{Z}_{1}} \end{equation} The backdoor paths from $X$ to $Z_{1}$ are as follows: \begin{equation} \begin{array}{l} 1) \, X \leftarrow U_{1} \rightarrow Y \leftarrow Z_{1} \newline 2) \, X \leftarrow U_{2} \rightarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \leftarrow Z_{1} \newline 3) \, X \leftarrow U_{2} \rightarrow Z_{2} \leftarrow U_{4} \rightarrow Y \leftarrow Z_{1} \newline 4) \, X \leftarrow Z_{2} \rightarrow Z_{3} \rightarrow Y \leftarrow Z_{1} \newline 5) \, X \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y \leftarrow Z_{1} \newline 6) \, X \leftarrow U_{3} \rightarrow Z_{3} \rightarrow Y \leftarrow Z_{1} \newline 7) \, X \leftarrow U_{3} \rightarrow Z_{3} \leftarrow Z_{2} \leftarrow U_{4} \rightarrow Y \leftarrow Z_{1} \end{array} \end{equation}
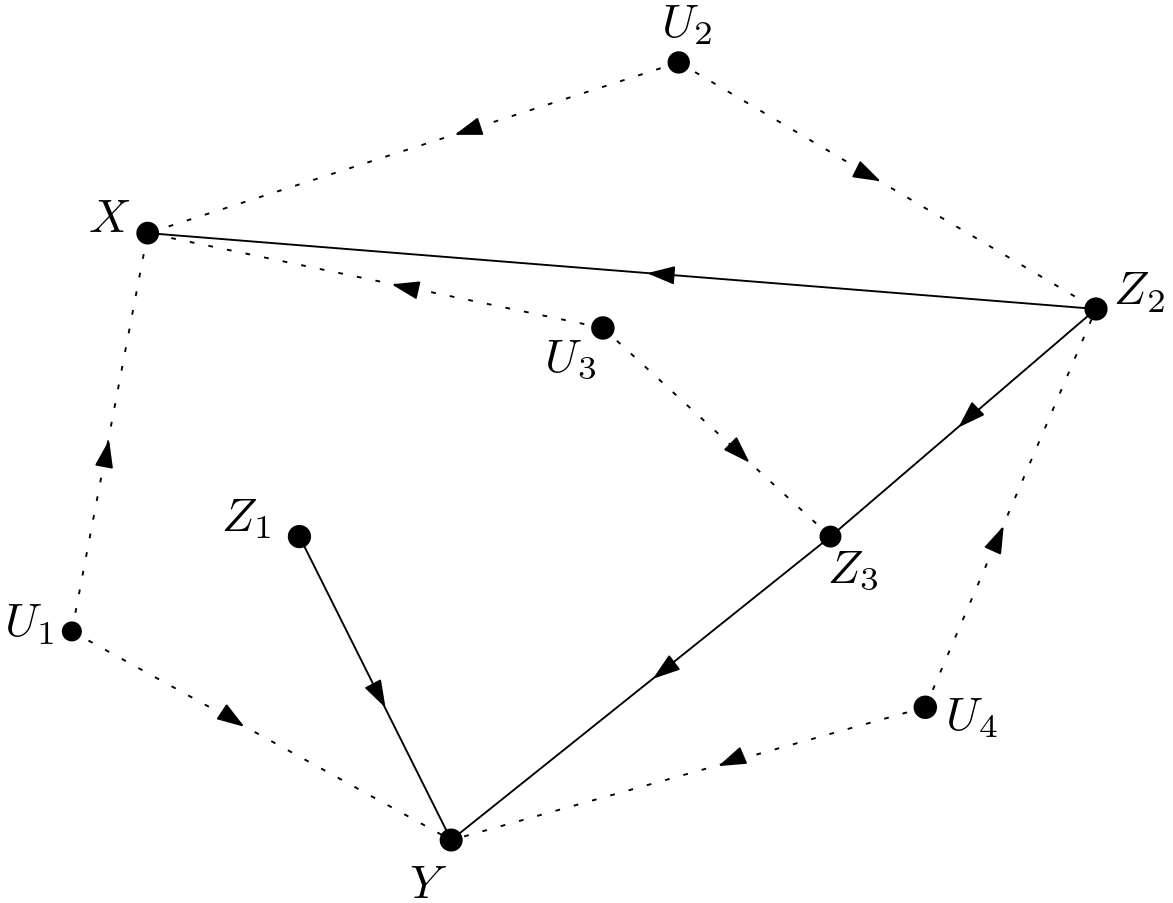
The first path is blocked due to the collider $U_{1} \rightarrow Y \leftarrow Z_{1}$. The second path is blocked due to conditioning on $Z_{2}$ or the collider $Z_{3} \rightarrow Y \leftarrow Z_{1}$. The third path is blocked due to the collider $U_{4} \rightarrow Y \leftarrow Z_{1}$. The fourth path is blocked due to conditioning on $Z_{2}$ or the collider $Z_{3} \rightarrow Y \leftarrow Z_{1}$. The fifth path is blocked due to conditioning on $Z_{2}$ or the collider $U_{4} \rightarrow Y \leftarrow Z_{1}$. The sixth path is blocked due to the collider $Z_{3} \rightarrow Y \leftarrow Z_{1}$. The seventh path is blocked due to the collider $U_{3} \rightarrow Z_{3} \leftarrow Z_{2}$ or conditioning on $Z_{2}$ or the collider $U_{4} \rightarrow Y \leftarrow Z_{1}$. Since all the backdoor paths from $X$ to $Z_{1}$ in $G_{\overline{Z}_{1}}$ are conditionally blocked given $Z_{2}$, $X$ and $Z_{1}$ are conditionally d-separated given $Z_{2}$ in $G_{\overline{Z}_{1}}$. Therefore, the intervention on $Z_{1}$ in $p\left(x^{\prime}| do\left(z_{1}\right),z_{2}\right)$ can be removed: \begin{equation} p\left(x^{\prime}| do\left(z_{1}\right),z_{2}\right)=p\left(x^{\prime}| z_{2}\right) \end{equation} As to $p\left(y|x^{\prime}, do\left(z_{1}\right),z_{2}\right)$, remembering the reasoning that led to the expansion in the equation (\ref{total_sum_on_X}), it is already known that $Z_{1}$ and $Y$ are conditionally d-separated given $X$ and $Z_{2}$. Hence, the intervention on $Z_{1}$ can be replaced with the observation of $Z_{1}$: \begin{equation} p\left(y|x^{\prime}, do\left(z_{1}\right),z_{2}\right)=p\left(y|x^{\prime}, z_{1}, z_{2}\right) \end{equation} As a result, the following equation can be written: \begin{equation} p\left(y|do\left(z_{1}\right),z_{2}\right)=\sum_{x^{\prime}} p\left(y|x^{\prime}, z_{1}, z_{2}\right)p\left(x^{\prime}| z_{2}\right) \end{equation} Hence, $p\left(y|z_{1}, z_{2}, do\left(x\right)\right)$ in the expansion in the equation (\ref{double_total_sum}) has been shown to satisfy the following equality: \begin{equation} p\left(y|z_{1}, z_{2}, do\left(x\right)\right)=\sum_{x^{\prime}}p\left(y|x^{\prime},z_{1},z_{2}\right)p\left(x^{\prime}|z_{2}\right) \end{equation} Now, it is the turn of $p\left(z_{2}|do\left(x\right)\right)$ in the expansion given in the equation (\ref{double_total_sum}). Can the intervention on $X$ be removed? The removal is possible if $X$ and $Z_{2}$ are d-separated in the graph $G_{\overline{X}}$. $G_{\overline{X}}$ is given in the Figure 4. The paths from $X$ to $Z_{2}$ are listed below: \begin{equation} \begin{array}{l} 1) \, X \rightarrow Z_{1} \leftarrow Z_{2} \newline 2) \, X \rightarrow Z_{1} \rightarrow Y \leftarrow Z_{3} \leftarrow Z_{2} \newline 3) \, X \rightarrow Z_{1} \rightarrow Y \leftarrow U_{4} \rightarrow Z_{2} \end{array} \end{equation} The first path is blocked since it is a collider and $Z_{1}$ is not conditioned on. The second path is blocked by the collider $Z_{1} \rightarrow Y \leftarrow Z_{3}$. The third path is also blocked due to the collider $Z_{1} \rightarrow Y \leftarrow U_{4}$. Therefore, $X$ and $Z_{2}$ are d-separated in the graph $G_{\overline{X}}$. This d-separation implies the following equality: \begin{equation} p\left(z_{2}|do\left(x\right)\right)=p\left(z_{2}\right) \end{equation} So, finally, all the post-intervention probabilities in the equation (\ref{double_total_sum}) have been written in terms of pre-intervention probabilities. They are wrapped up as follows: \begin{equation} p\left(y|z_{1}, z_{2}, do\left(x\right)\right)=\sum_{x^{\prime}}p\left(y|x^{\prime},z_{1},z_{2}\right)p\left(x^{\prime}|z_{2}\right) \end{equation} \begin{equation} p\left(z_{1}|z_{2},do\left(x\right) \right)=p\left(z_{1}|z_{2},x \right) \end{equation} \begin{equation} p\left(z_{2}|do\left(x\right)\right)=p\left(z_{2}\right) \end{equation} The causal effect of $X$ on $Y$ has been proven to satisfy the following: \begin{equation} p\left(y|do\left(x\right)\right) = \sum_{z_{1}} \sum_{z_{2}} p\left(y|z_{1},z_{2},do\left(x\right)\right) p\left(z_{1}|z_{2},do\left(x\right)\right)p\left(z_{2}|do\left(x\right)\right) \Rightarrow \end{equation} \begin{equation} p\left(y|do\left(x\right)\right) = \sum_{z_{1}} \sum_{z_{2}}\sum_{x^{\prime}}p\left(y|x^{\prime},z_{1},z_{2}\right)p\left(x^{\prime}|z_{2}\right)p\left(z_{1}|z_{2},x \right)p\left(z_{2}\right) \end{equation}
Conclusion
A causal effect which cannot be calculated using the backdoor criterion or simple application of the rules of the do-calculus has been demonstrated to be calculated by means of the topology of the graph. A subgraph of the problem graph is known to be an identifying graph. The know-how for this subgraph has been used to calculate the causal effect under investigation.
References
[1] Judea Pearl, Causality: Models, Reasoning and Inference, Cambridge University Press, 2009.