Introduction
In this article, a lemma is to be proven. This lemma is used in the proof of a theorem in the article given in the reference [1]. Although the lemma is proven in [1], I could not understand it and I am going to prove it myself.
The Theorem And The Lemma And The Proof
The theorem is about finding an admissible sequence and is as follows:
Theorem If there is an admissible sequence $Z_{1}^{*}, … , Z_{n}^{*}$, then for every minimally admissible subsequence $Z_{1}, … , Z_{k-1}$, there is an admissible set $Z_{k}$.
The proof of this theorem is based on two lemmas the first of which is the following:
Lemma For any DAG $G$ and any two disjoint subsets of nodes $X$ and $Y$, let the ancestor-set of $\left(X,Y\right)$, denoted $A\left(X,Y\right)$, be the set of nodes which have a descendant in either $X$ or $Y$.
The following two separation conditions hold for any two sets of nodes $W$ and $Z$:
\begin{equation} \left ( Y\text{ d-separated from } X|Z, W \cap A\left(X,Y \right )\right)_{G} \text{ whenever } \left ( Y \text{ d-separated from } X | Z \right )_{G} \label{lemma11} \end{equation}
\begin{equation} \left ( Y\text{ d-separated from } X|W \cap A\left(X,Y \right )\right)_{G} \text{ whenever } \left ( Y \text{ d-separated from } X | W \right )_{G} \label{lemma12} \end{equation} What is the meaning of the equation \eqref{lemma11}? If there is a conditional d-separation between $X$ and $Y$, augmenting the condition set with a variable or variables from $A\left(X,Y\right)$ does not destroy the d-separation and maintain it. What is the meaning of the equation \eqref{lemma12}? It is known that $X$ and $Y$ are conditionally d-separated given $W$. If $W \cap A \left(X,Y\right)=\emptyset$, then the independence of $X$ and $Y$ can be destroyed because it is not known if $X$ and $Y$ are d-separated. But a nonempty intersection will imply variables from the set $W$ and maintain the independence. So, conditioning on variables from $A\left(X,Y\right)$ does not harm d-separation.
Let lemma 1’s first part given in the equation \eqref{lemma11} be proven. It is known that $\left(Y \text{ d-separated from } X|Z\right)_{G}$. It is to be proven that $\left(Y \text{ d-separated from } X|Z, w\right)_{G}$ is still true if $w$ is an element of $A\left(X,Y\right)$.
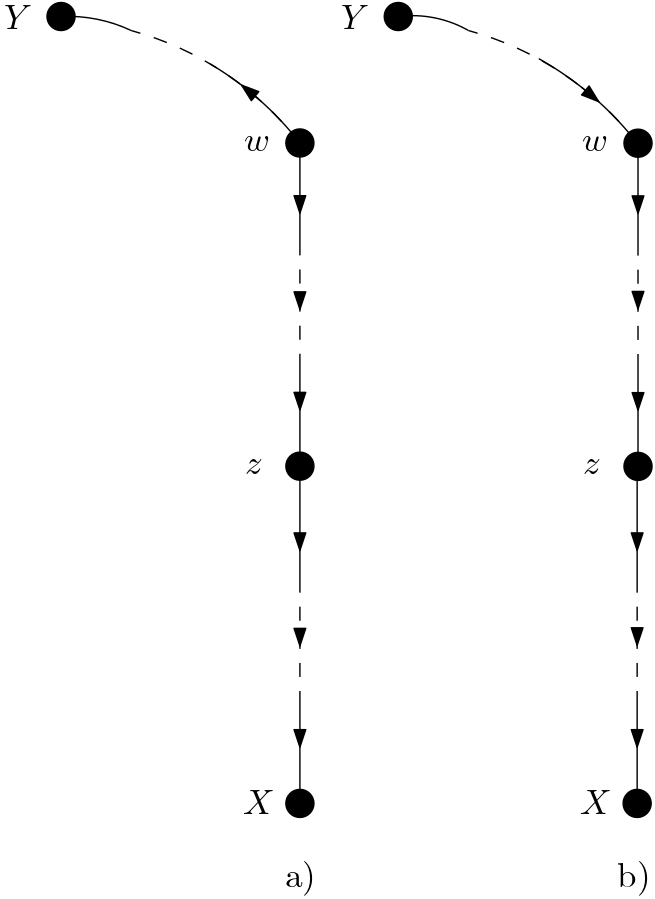
Let the first probable setting be described. $w$ is an ancestor of only $X$. Since $w$ is an ancestor of $X$, there must be a causal path from $w$ to $X$. $z$ is on the causal path from $w$ to $X$. Within this setting there are two possibilities for $Y$. The first possibility is that the blocked path between $X$ and $Y$ contains $w$. As shown in the Figure 1a, $w$ can be the center node of a fork. Conditioning on $w$ blocks this fork and does not harm the conditional d-separation of $X$ and $Y$ given $z$. $w$ can be the intermediate node of a chain as in the Figure 1b. Conditioning on $w$ blocks this chain and does not change the conditional d-separation of $X$ and $Y$ given $z$.
The second possibility is that $w$ is not on the blocked path between $X$ and $Y$. There are four cases for this possibility. These cases are shown in the Figure 2.
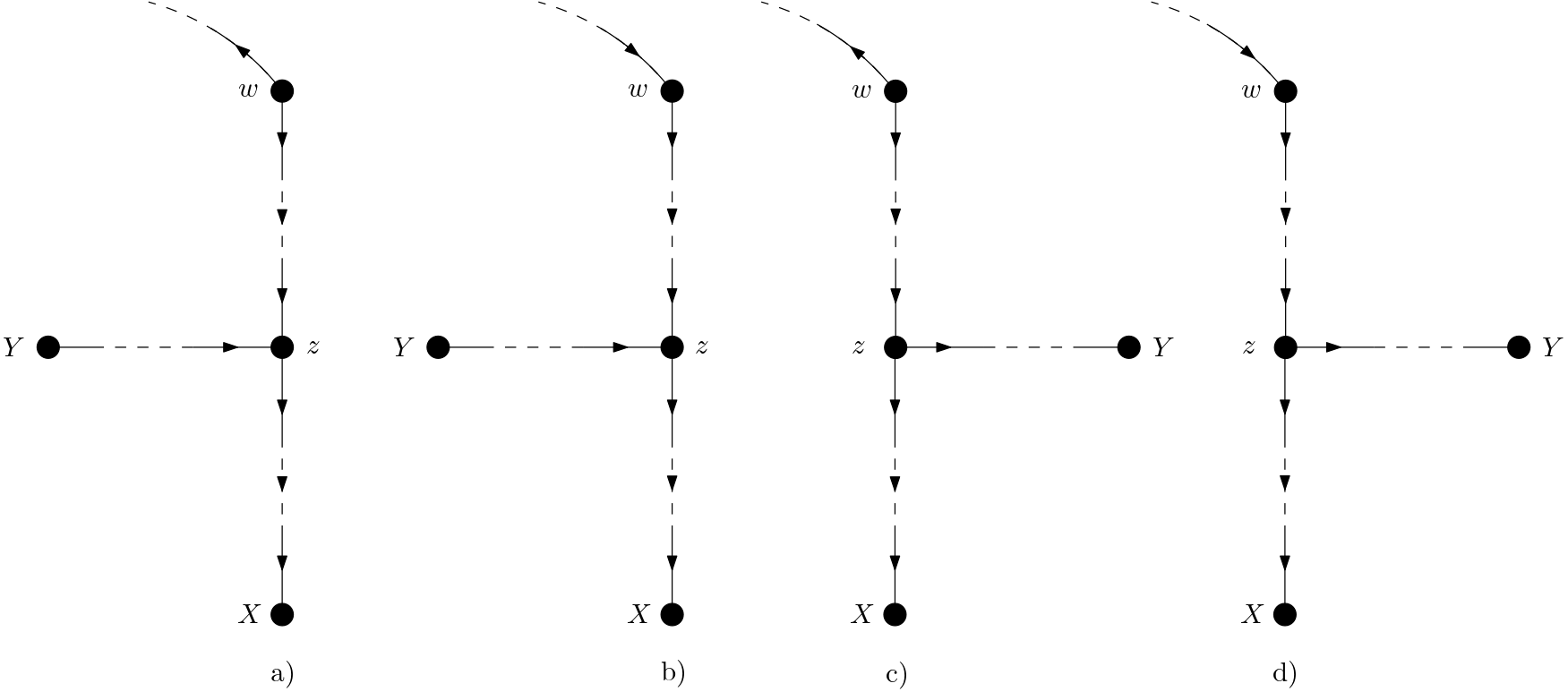
In none of the cases shown in the Figure 2, conditioning on $w$ changes the fact that the path between $X$ and $Y$ is blocked because conditioning on $w$ only blocks the causal path from $w$ to $X$.
For the cases shown in the Figure 1 and the Figure 2, can’t a path blocked by a collider whose colliding node is $w$ be opened by conditioning on $w$? No, because $z$ is a descendant of $w$ and it is already known that conditioning on $z$ d-separates $X$ and $Y$. If there were such a collider, then conditioning on $z$ which is a descendant of the collider node $w$ would open the collider and d-connect $X$ and $Y$. But this is a contradiction with the already known fact that conditioning on $z$ d-separates $X$ and $Y$.
The first probable setting can be adapted to the case where $w$ is an ancestor of only $Y$. Nothing changes in the logic of the proof, the same arguments are valid as can be easily confirmed.
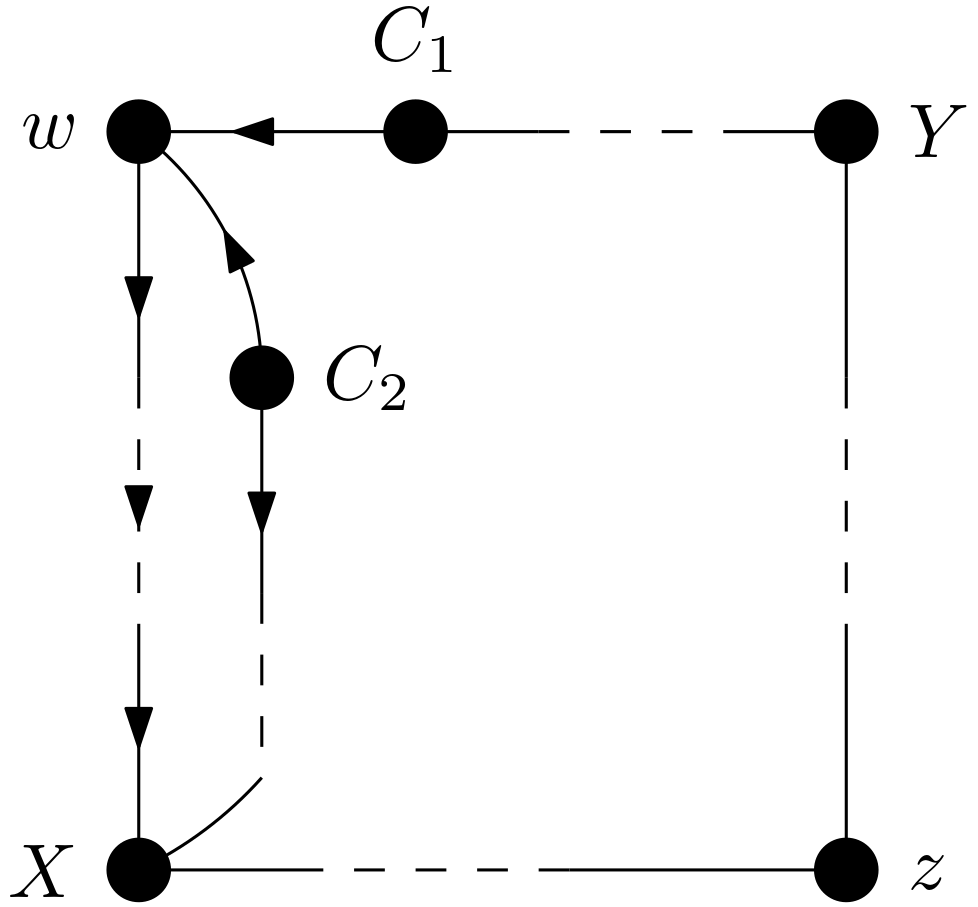
Let the second probable setting be described. $w$ is an ancestor of only $X$. Therefore, there is a causal path from $w$ to $X$. $z$ is not on the causal path from $w$ to $X$ this time. In this setting, there are two possibilities for $Y$. The first possibility is that $w$ is on a path between $X$ and $Y$. This path does not contain $z$. Let this path be called $P$. Since it is known that $\left(Y \text{ d-separated from } X|Z\right)_{G}$, $P$ is known to be blocked. If also $w$ is conditioned on, can $P$ be unblocked? Unblocking can occur if $P$ is blocked due to a collider whose collider node is $w$. Can such a collider exist? In the Figure 3, such a collider which is $C_{1} \rightarrow w \leftarrow C_{2}$ is shown. The causal path $C_{1} \rightarrow w \rightarrow … \rightarrow X$ is unblocked before $w$ is conditioned on in addition to the conditioning on $z$. And this makes $X$ and $Y$ d-connected. But this is in conflict with the known fact that $\left(Y \text{ d-separated from } X|Z\right)_{G}$. Due to this contradiction, such a collider cannot exist.
The second possibility of this case is that $w$ is not on a path between $X$ and $Y$. It should be obvious that conditioning on $w$ does not affect the conditional d-separation of $X$ and $Y$ given $z$ since $w$ does not interfere with any paths between $X$ and $Y$.
The second probable setting can be adapted to the case where $w$ is an ancestor of only $Y$. Nothing changes in the logic of the proof, the same arguments are valid as can be easily confirmed.
Let the third probable setting be described. $w$ is an ancestor of both $X$ and $Y$. The four possibilities are shown in the Figure 4. In the Figure 4a, $z$ is on the causal paths from $w$ to $X$ and $Y$. In the Figure 4b, $z$ is on the causal path from $w$ to $X$. In the Figure 4c, $z$ is on the causal path from $w$ to $Y$. In the Figure 4d, $z$ is not on any of the causal paths from $w$ to $X$ and $w$ to $Y$.
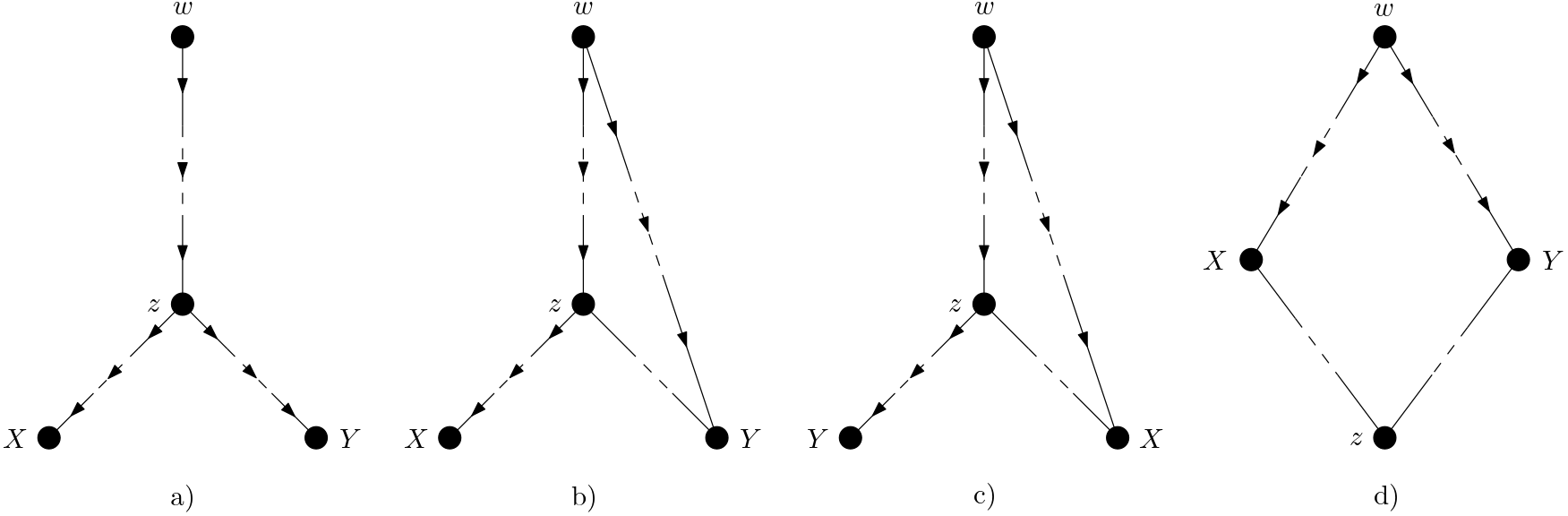
For the cases in a), b) and c), can conditioning also on $w$ make $X$ and $Y$ d-connected while conditioning on $z$ d-separates $X$ and $Y$? This could happen if there were a path between $X$ and $Y$ and this path were blocked by a collider whose collider node were $w$. If there were such a collider, conditioning on $z$ would open this collider and the path blocked by this collider since $z$ is a descendant of $w$. But this will cause a contradiction to the already known fact that $X$ and $Y$ are conditionally d-separated given $z$. So, such a collider cannot exist. As to the case in d), can conditioning also on $w$ d-connect $X$ and $Y$ while $z$ is conditioned on? If there were a collider whose collider node were $w$ and this collider blocked a path between $X$ and $Y$, conditioning on $w$ would make $X$ and $Y$ d-connected while $z$ is conditioned-on. But, can there be such a collider? Such a collider is shown in the Figure 5.
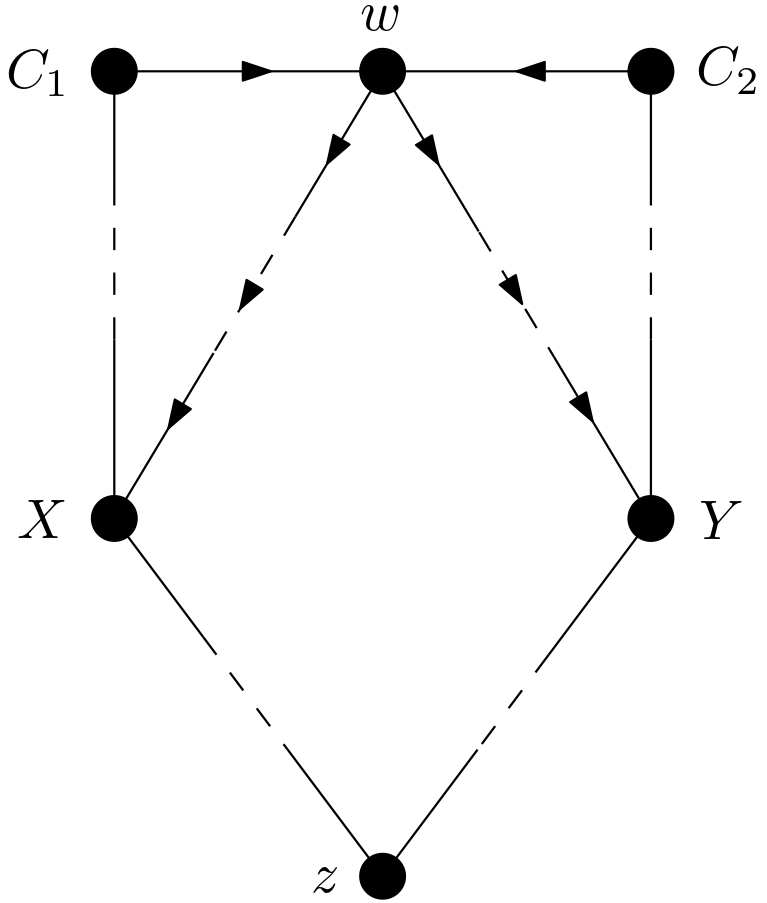
It is assumed that conditioning on $w$ d-connects $X$ and $Y$ through the path $X —– … —– \ C_{1} \rightarrow w \leftarrow C_{2} \ —– … —– \ Y$. Then, both of the paths $X —– … —– \ C_{1} \rightarrow w$ and $w \leftarrow C_{2} \ —– … —– \ Y$ are assumed to be unblocked. But then, before conditioning on $w$, $X$ and $Y$ will be d-connected by means of either $X —– … —– \ C_{1} \rightarrow w \rightarrow … \rightarrow Y$ or $X \leftarrow … \leftarrow w \leftarrow C_{2} \ —– … —– \ Y$. These d-connections will be in contradiction with the already known fact that $X$ and $Y$ are conditionally d-separated given $z$. As a result, such a collider cannot exist.
Now, let lemma 1’s second part given in the equation \eqref{lemma12} be proven. In fact, there is not much to prove. It is known that $\left(Y \text{ d-separated from }X|W \right)_{G}$. $W \cap A\left(X,Y\right)$ contains a variable from $W$ if the intersection is nonempty. Then, $Y$ will be d-separated from $X$ due to the fact that $\left(Y \text{ d-separated from }X|W \right)_{G}$. If $W \cap A\left(X,Y\right) =\emptyset$, then $Y$ can be d-connected to $X$ since it is not known for sure if $Y \text{ d-separated from } X$.
Conclusion
It has been proven that conditioning on ancestors of two disjoint sets of variables which are conditionally d-separated given another set $Z$ does not harm this d-separation.
References
[1] Judea Pearl and James Robins. Probabilistic evaluation of sequential plans from causal models with hidden variables. In Proceedings of the Eleventh conference on Uncertainty in artificial intelligence, pages 444-453, 1995.