Introduction
In this article, it is explained which variables cause statistical variations in a counterfactual within the causality framework of Judea Pearl. After the explanation, the counterfactual interpretation of the backdoor criterion is elaborated on. The statistical variations in a counterfactual and the counterfactual interpretation of the backdoor criterion are written about on page 102 of [1]. However, in my opinion, there should be more explanation.
The Problem
There is a directed acyclic graph (DAG). Two of the variables in this DAG are $X$ and $Y$. The reasons for the statistical variations in the counterfactual $Y_{X=x}$ are to be determined. In other words, the answer to the question which variables cause statistical variations in the counterfactual $Y_{X=x}$ is to be explained. Then, the counterfactual interpretation of the backdoor criterion is to be examined in a detailed manner.
The Explanation
If there is a flow of information between two variables in a DAG, then these two variables can affect each other statistically. This fact answers the question which variables cause statistical variations in the counterfactual $Y_{X=x}$. There must be a flow of information between $Z$ and $Y_{X=x}$ for $Z$ to cause statistical variations in $Y_{X=x}$. The flow of information is possible when $Z$ and $Y_{X=x}$ are d-connected. Therefore, if a variable blocks this flow of information, then there will be no statistical variation in $Y_{X=x}$. Which variables block the flow of information to $Y_{X=x}$ the most or from maximum number of variables? These variables are the parents of $Y_{X=x}$. So, if the parents of $Y_{X=x}$ are conditioned on, then there will be no statistical variation in $Y_{X=x}$. In other words, assume that all the parents of $Y_{X=x}$ are conditioned on except one, then the statistical variations in $Y_{X=x}$ will be transmitted by that one parent.
Let the DAG in the Figure 4.4a of [1] be drawn in the Figure 1. Let this DAG be called $G$.
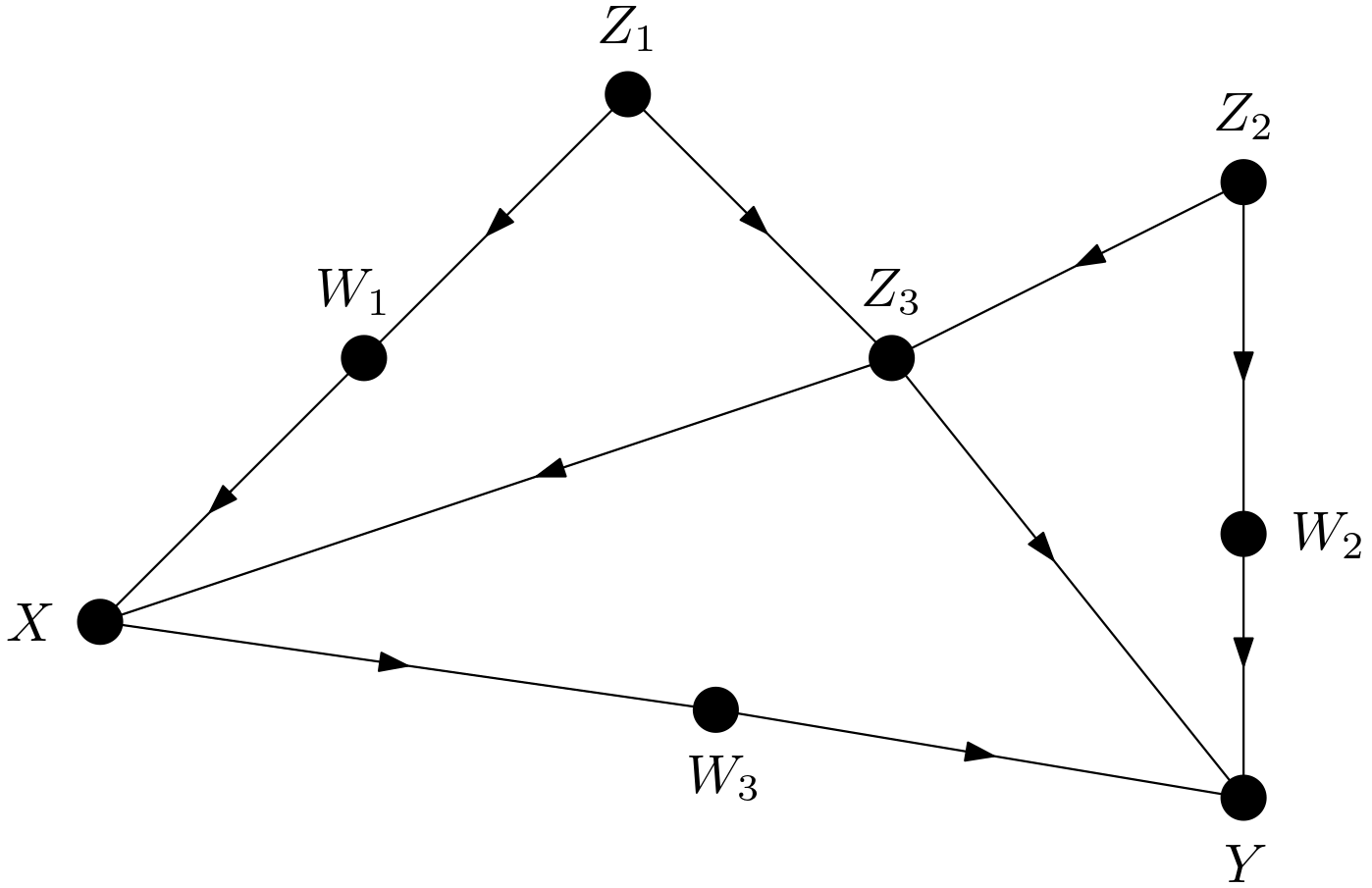
Now, let the variables causing statistical variations in $Y_{X=x}$ be determined. The DAG corresponding to this counterfactual is $G_{\overline{X}}$. It is presented in the Figure 2.
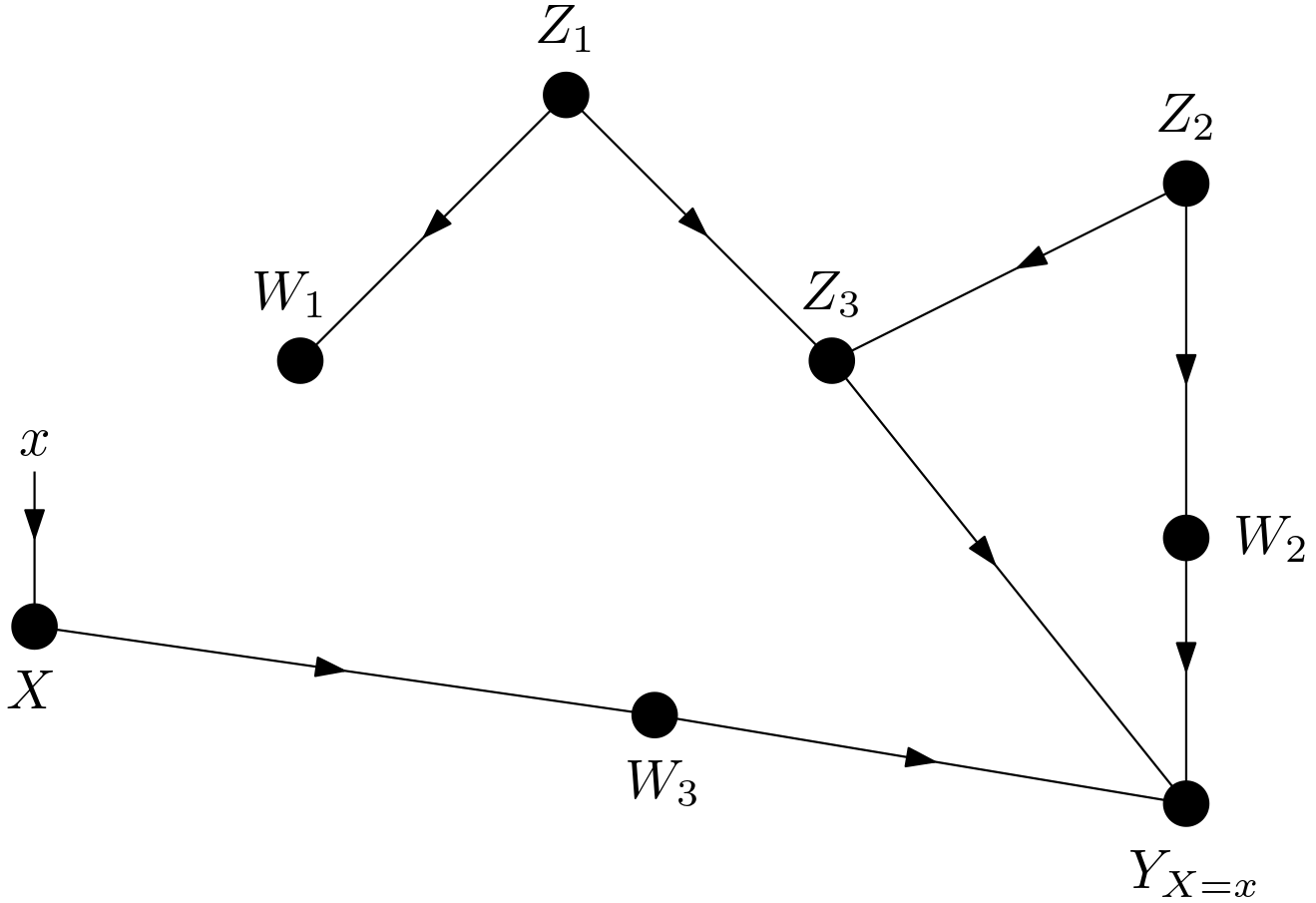
The variables which are d-connected to $Y_{X=x}$ in the DAG $G_{\overline{X}}$ are to be determined. $W_{1}$ is d-connected to $Y_{X=x}$ by means of the path $W_{1} \leftarrow Z_{1} \rightarrow Z_{3} \rightarrow Y_{X=x}$. Hence, $W_{1}$ can create a statistical variation in $Y_{X=x}$. $Z_{1}$ is d-connected to $Y_{X=x}$ by means of the path $Z_{1} \rightarrow Z_{3} \rightarrow Y_{X=x}$. So, $Z_{1}$ can create a statistical variation in $Y_{X=x}$. $Z_{3}$ is a parent of $Y_{X=x}$, which means that it can also create a statistical variation in $Y_{X=x}$. $Z_{2}$ is d-connected to $Y_{X=x}$ by means of the paths $Z_{2} \rightarrow Z_{3} \rightarrow Y_{X=x}$ and $Z_{2} \rightarrow W_{2} \rightarrow Y_{X=x}$. That’s why $Z_{2}$ can create a statistical variation in $Y_{X=x}$. $W_{2}$ is a parent of $Y_{X=x}$ and it can create a statistical variation in $Y_{X=x}$. $W_{3}$ is a parent of $Y_{X=x}$. Hence, $W_{3}$ is expected to create a statistical variation in the counterfactual. However, $W_{3}$ is a special parent of the counterfactual. It is on the causal path from $X$ to the counterfactual $Y_{X=x}$. Since $X$ is constant at $x$, any variation in $W_{3}$ is in fact due to a variation of $U_{W_{3}}$. Hence, $U_{W_{3}}$ rather than $W_{3}$ can actually create a statistical variation in $Y_{X=x}$.
As to the exogenous variables in the DAG, $U_{W_{1}}$ cannot create a statistical variation in $Y_{X=x}$ since it is d-separated from the counterfactual due to the collider $U_{W_{1}} \rightarrow W_{1} \leftarrow Z_{1}$. $U_{Z_{1}}$ is equal to $W_{1}$. $U_{Z_{3}}$ can create a statistical variation in $Y_{X=x}$ because it is d-connected to the counterfactual by means of the path $U_{Z_{3}} \rightarrow Z_{3} \rightarrow Y_{X=x}$. $U_{Z_{2}}$ is equal to $Z_{2}$. $U_{W_{2}}$ can create a statistical variation in $Y_{X=x}$ since it is d-connected to the counterfactual by the path $U_{W_{2}} \rightarrow W_{2} \rightarrow Y_{X=x}$. $U_{W_{3}}$ was mentioned in the previous paragraph. There is no $U_{X}$ since $X$ is intervened on. $U_{Y}$ is a parent of $Y_{X=x}$. Hence, it can create a statistical variation in the counterfactual.
The Counterfactual Interpretation Of The Backdoor Criterion
It is particularly important to examine the causal path from $X$ to $Y_{X=x}$ while studying how statistical variations are created in the counterfactual. The reason is that this path can cause some difficulties while understanding the counterfactual interpretation of the backdoor criterion. In the DAG given in the Figure 2, the causal path from $X=x$ to $Y_{X=x}$ contains only one intermediate variable which is $W_{3}$. In order to examine a more general case, assume that there is a new DAG in which the causal path from $X$ to $Y_{X=x}$ is as shown in the Figure 3.

$X$ is constant at $x$. Hence, any variation in $W_{1}$ is due to $U_{W_{1}}$. Any variation in $W_{2}$ is due to the variation in $W_{1}$ and $U_{W_{2}}$. The variation in $W_{1}$ is due to $U_{W_{1}}$. Then, any variation in $W_{2}$ is due to $U_{W_{1}}$ and $U_{W_{2}}$. Any variation in $W_{3}$ is due the variation in $W_{2}$ and $U_{W_{3}}$. The variation in $W_{2}$ is due to $U_{W_{1}}$ and $U_{W_{2}}$. Hence, any variation in $W_{3}$ is due to $U_{W_{1}}$, $U_{W_{2}}$ and $U_{W_{3}}$. Any variation in $Y_{X=x}$ is due to the variation in $W_{3}$ and its other parents in the rest of the DAG. The variation in $W_{3}$ is due to $U_{W_{1}}$, $U_{W_{2}}$ and $U_{W_{3}}$. Therefore, any variation in $Y_{X=x}$ is due to $U_{W_{1}}$, $U_{W_{2}}$, $U_{W_{3}}$ and the counterfactual’s other parents in the DAG. This analysis can easily be broadened to the case of a causal path from $X$ to $Y_{X=x}$ with any number of intermediate variables. As a result, the parents of intermediate variables on the causal path from $X$ to $Y_{X=x}$ causes or transmits statistical variation to $Y_{X=x}$.
Now, let the counterfactual interpretation of the backdoor criterion be examined. The counterfactual interpretation requires the knowledge of the variables which can transmit statistical variation to the counterfactual. The transmission of statistical variation to the counterfactual has been studied so far. Hence, there is no problem with making the interpretation. When the variables satisfying the backdoor condition for the ordered pair $\left(X, Y\right)$ are conditioned on, the backdoor paths from $X$ to $Y$ are blocked. This means that the backdoor paths from $X$ to $Y_{X=x}$ are also blocked. This also means that the backdoor paths from $X$ to the parents of $Y_{X=x}$ are blocked. The parents on the causal paths from $X$ to $Y_{x=x}$ are excluded from the parents which are on the blocked backdoor paths. So, there can be no statistical variation transmission from $X$ to the parents on the blocked backdoor paths, which implies that $X$ and $Y_{X=x}$ are d-separated by these blocked backdoor paths.
As to the causal paths from $X$ to $Y_{X=x}$, the parents of the intermediate variables on the causal paths are in fact already d-separated from $X$. Let some examples be given from the causal path given in the Figure 3. $U_{W_{1}}$ is d-separated from $X$ due to the collider $X \rightarrow W_{1} \leftarrow U_{W_{1}}$. $U_{W_{2}}$ is d-separated from $X$ due to the collider $W_{1} \rightarrow W_{2} \leftarrow U_{W_{2}}$. $U_{W_{3}}$ is d-separated from $X$ due to the collider $W_{2} \rightarrow W_{3} \leftarrow U_{W_{3}}$. Although $Y_{X=x}$ is not an intermediate variable, it should be mentioned that $U_{Y}$ is also d-separated from $X$ due to the collider $W_{3} \rightarrow Y_{X=x} \leftarrow U_{Y}$. So, a parent of an intermediate variable is d-separated from $X$ due to the collider whose collider node is the intermediate variable, whose colliding nodes are the parent and the previous intermediate node. It has been shown that the parents of the intermediates nodes transmit statistical variations from $X$ to the counterfactual. And it has just been shown that these parents are d-separated from $X$. Hence, $X$ cannot transmit any statistical variation to $Y_{X=x}$ through these parents. $X$ cannot transmit statistical variation to $Y_{X=x}$ through $U_{Y}$, either.
As a result, there is no way for $X$ to transmit or cause statistical variation to $Y_{X=x}$ if the backdoor criterion is satisfied. This result implies the conditional independence of $X$ and $Y_{X_x}$ given the set $Z$ of variables satisfying the backdoor condition: \begin{equation} P\left(Y_{X=x}|Z, X\right)=P\left(Y_{X=x}|Z\right) \end{equation}
Conclusion
It has been studied how the statistical variation in a counterfactual are caused. Then, the counterfactual interpretation of the backdoor criterion has been elaborated on.
References
[1] Judea Pearl, Madelyn Glymour, Nicholas P. Jewell, “Causal Inference In Statistics A Primer”, Wiley, 2016.