Introduction
In this article, interventional expectations and counterfactual expectations are to be studied within the causal inference framework of Judea Pearl. The SCM of the example is from the page 99 of [1].
The Example
The structural causal model (SCM) of this example is from the page 99 of [1]. It is as follows: \begin{gather} X=U_{1} \notag \newline Z=2X+U_{2} \label{SCM1} \newline Y=3Z \notag \end{gather} However, tha data set is different. It is assumed that $U_{1}$ and $U_{2}$ take values from the set $\left \lbrace 0, \frac{1}{2}, 1\right \rbrace$. There are 9 possible $\left(u_{1},u_{2}\right)$ tuples. Let they be equally probable. The data set that is generated by the SCM is shown in the Table 1. \begin{array}{cccccc} u_{1} & u_{2} & P\left(u_{1},u_{2}\right) & x & z & y \newline 0 & 0 & \frac{1}{9} & 0 & 0 & 0 \newline 0 & \frac{1}{2} & \frac{1}{9} & 0 & \frac{1}{2} & \frac{3}{2} \newline 0 & 1 & \frac{1}{9} & 0 & 1 & 3 \newline \frac{1}{2} & 0 & \frac{1}{9} & \frac{1}{2} & 1 & 3 \newline \frac{1}{2} & \frac{1}{2} & \frac{1}{9} & \frac{1}{2} & \frac{3}{2} & \frac{9}{2} \newline \frac{1}{2} & 1 & \frac{1}{9} & \frac{1}{2} & 2 & 6 \newline 1 & 0 & \frac{1}{9} & 1 & 2 & 6 \newline 1 & \frac{1}{2} & \frac{1}{9} & 1 & \frac{5}{2} & \frac{15}{2} \newline 1 & 1 & \frac{1}{9} & 1 & 3 & 9 \newline \notag \end{array}
Table 1: The data set generated by the SCM in the equation \eqref{SCM1}.
Now, let the following interventional expectation be calculated:
\begin{equation}
E\left [Y | do\left(X=1\right), Z=2 \right ] = ?
\end{equation}
When the intervention $do\left(X=1\right)$ is applied, the SCM in the equation
\eqref{SCM1} is changed to the following new SCM:
\begin{gather}
X=1 \notag \newline
Z=2+U_{2} \label{SCM1Interven1} \newline
Y=3Z \notag
\end{gather}
The data set created by the SCM in the equation \eqref{SCM1Interven1} is presented
in the Table 2.
\begin{array}{ccccc}
u_{2} & P\left(u_{2}\right) & x & z & y \newline
0 & \frac{1}{3} & 1 & 2 & 6 \newline
\frac{1}{2} & \frac{1}{3} & 1 & \frac{5}{2} & \frac{15}{2} \newline
1 & \frac{1}{3} & 1 & 3 & 9 \newline
\notag
\end{array}
Table 2: The data set created by the SCM in the equation \eqref{SCM1Interven1}.
When the condition $Z=2$ is imposed, the data in the Table 2 is filtered with the $Z=2$ condition and only the first row remains. Therefore, the interventional expectation is found as follows: \begin{equation} E\left [Y | do\left(X=1\right), Z=2 \right ] = 6 \label{intervenExpect1Res1} \end{equation} Let this result be also found using the rules of do-calculus which are given on page 85 of [2]. First, $P\left(Y|do(X=1), Z=2\right)$ is to be found. The DAG of the SCM in the equation \eqref{SCM1} is shown in the Figure 1.
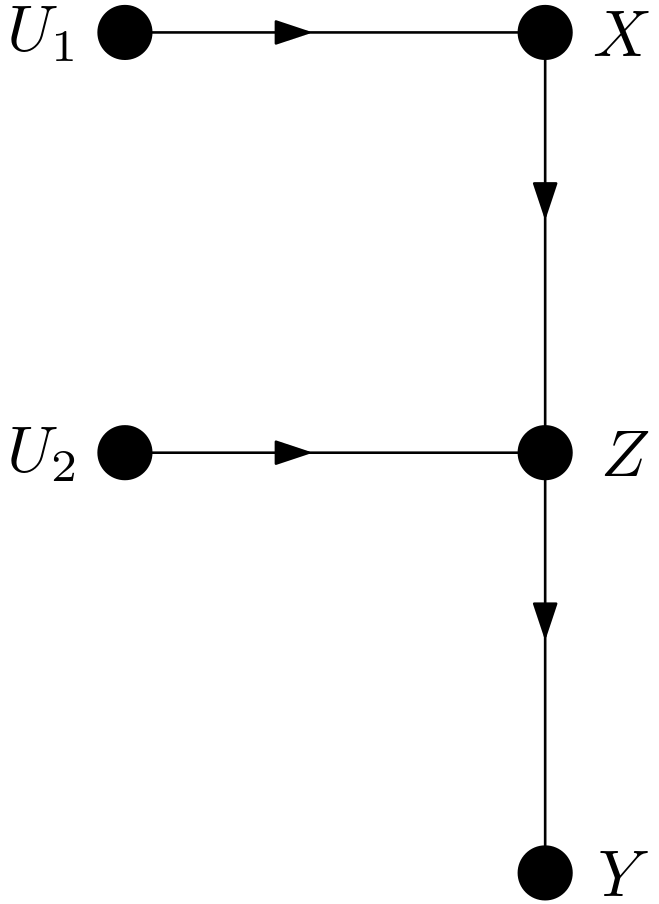
Figure 1: The data set created by the SCM in the equation \eqref{SCM1Interven1}.
Can the intervention on $X$ in $P\left(Y|do(X=1), Z=2\right)$ be replaced with observing $X$? This replacement is possible if \begin{equation} \left(\left(Y \text{ d-separated from } X\right) | Z\right) \text{ in } G_{\underline{X}} \label{doCalc1} \end{equation} according to the second rule of do-calculus. $G_{\underline{X}}$ is presented in the Figure 2.
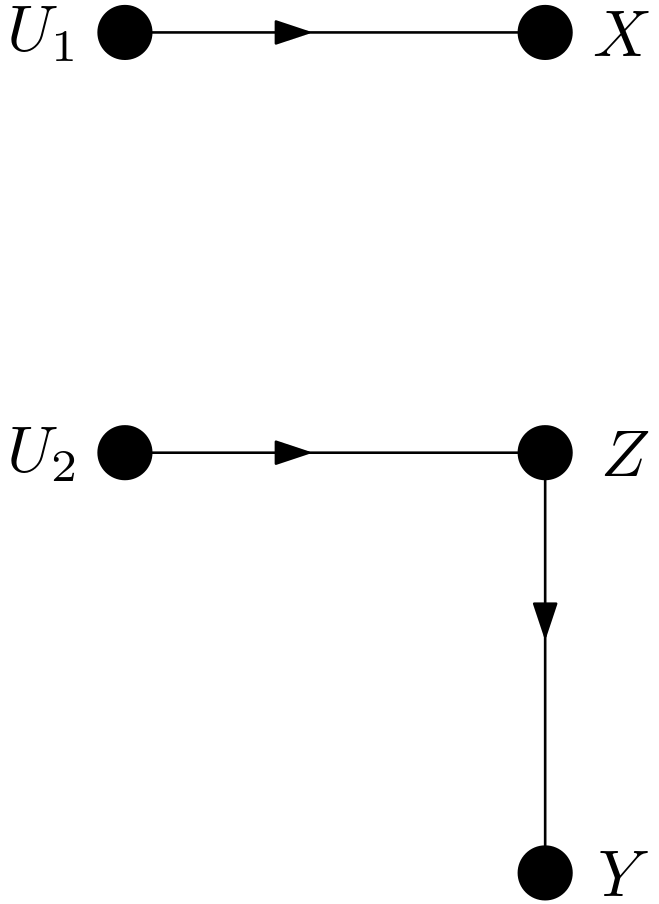
Figure 2: The DAG $G_{\underline{X}}$.
It is easily seen that $Y$ is conditionally d-separated from $X$ given $Z$, which means that the condition in the equation \eqref{doCalc1} is satisfied. Therefore, the following equality can be written: \begin{equation} P\left(Y|do\left(X=1\right),Z=2\right)= P\left(Y|X=1,Z=2\right) \end{equation} If the data set in the Table 1 is considered, then the following equality can be written: \begin{equation} P\left(Y|X=1, Z=2\right)= \begin{cases} 1 & \text{if } Y=6 \newline 0 & \text{otherwise} \end{cases} \Rightarrow P\left(Y|do\left(X=1\right), Z=2\right)= \begin{cases} 1 & \text{if } Y=6 \newline 0 & \text{otherwise} \end{cases} \end{equation} Therefore, the interventional expectation $E\left[Y|do\left(X=1\right),Z=2\right]$ is expressed as follows: \begin{equation} E\left[Y|do\left(X=1\right),Z=2\right]= \sum_{y} P\left(Y=y|do\left(X=1\right),Z=2\right)y= \sum_{y} P\left(Y=y|X=1,Z=2\right)y=1\times 6 \Rightarrow \end{equation} \begin{equation} E\left[Y|do\left(X=1\right),Z=2\right]=6 \label{intervenExpect1Res2} \end{equation} The same result as the one in the equation \eqref{intervenExpect1Res1} has been obtained. The second interventional expectation to be calculated is as follows: \begin{equation} E\left [Y | do\left(X=0\right), Z=2 \right ] = ? \end{equation} The SCM corresponding to the intervention $do\left(X=0\right)$ is obtained from the SCM in the equation \eqref{SCM1} as follows: \begin{gather} X=0 \notag \newline Z=U_{2} \label{SCM1Interven2} \newline Y=3Z \notag \end{gather} The data set created by the SCM in the equation \eqref{SCM1Interven2} is shown in the Table 3. \begin{array}{ccccc} u_{2} & P\left(u_{2}\right) & x & z & y \newline 0 & \frac{1}{3} & 0 & 0 & 0 \newline \frac{1}{2} & \frac{1}{3} & 0 & \frac{1}{2} & \frac{3}{2} \newline 1 & \frac{1}{3} & 0 & 1 & 3 \newline \notag \end{array}
Table 3: The data set created by the SCM in the equation \eqref{SCM1Interven2}.
When the condition $Z=2$ is imposed, the data set is filtered for $Z=2$ and no row remains. Hence, the interventional expectation is obtained as follows: \begin{equation} E\left [Y | do\left(X=0\right), Z=2 \right ] = 0 \label{intervenExpect2Res1} \end{equation} Let this interventional expectation be also calculated using the rules of do-calculus in the same way as the one for the first interventional expectation. Since $Y$ is conditionally d-separated from $X$ given $Z$, \begin{equation} P\left(Y|do\left(X=0\right), Z=2\right)= P\left(Y|X=0, Z=2\right) \end{equation} When the data set in the Table 1 is taken into account, the following can be concluded: \begin{equation} P\left(Y|X=0, Z=2\right)=0 \Rightarrow P\left(Y|do\left(X=0\right), Z=2\right)=0 \end{equation} Therefore, \begin{equation} E\left [Y | do\left(X=0\right), Z=2 \right ] = 0 \label{intervenExpect2Res2} \end{equation} is again reached just like the result in the equation \eqref{intervenExpect2Res1}.
Let the two interventional expectations be summed up as follows: \begin{gather} E\left [Y | do\left(X=1\right), Z=2 \right ] = 6 \newline E\left [Y | do\left(X=0\right), Z=2 \right ] = 0 \end{gather}
Now, let the first counterfactual expectation be dealt with. It is as follows: \begin{equation} E\left[Y_{X=1}|Z=2\right]=? \end{equation} Let the condition $Z=2$ be applied to the data set in the Table 1. The new data set is a subset in which $Z=2$. It is displayed in the Table 4. \begin{array}{cccccc} u_{1} & u_{2} & P\left(u_{1},u_{2}\right) & x & z & y \newline \frac{1}{2} & 1 & \frac{1}{2} & \frac{1}{2} & 2 & 6 \newline 1 & 0 & \frac{1}{2} & 1 & 2 & 6 \newline \notag \end{array}
Table 4: The data set which is the result of filtering the set in the Table 1 with the condition $Z=2$.
Let the antecedent $X=1$ be employed. From the SCM in the equation \eqref{SCM1}, the following SCM is obtained for the antecedent $X=1$: \begin{gather} X=1 \notag \newline Z=2+U_{2} \label{SCM1Counter1} \newline Y=3Z \notag \end{gather} According to the Table 4 and the SCM in the equation \eqref{SCM1Counter1}, the data set given in the Table 5 is generated. \begin{array}{ccccc} u_{2} & P\left(u_{2}\right) & x & z & y \newline 1 & \frac{1}{2} & 1 & 3 & 9 \newline 0 & \frac{1}{2} & 1 & 2 & 6 \newline \notag \end{array}
Table 5: The data set which is generated for the antecedent $X=1$ according to the Table 4 and the SCM in the equation \eqref{SCM1Counter1}.
The counterfactual expectation can then be calculated as follows: \begin{equation} E\left[Y_{X=1}|Z=2\right]=\frac{1}{2}\times 9+\frac{1}{2}\times 6 \Rightarrow E\left[Y_{X=1}|Z=2\right]=\frac{15}{2} \end{equation} Now, the following counterfactual expectation is to be calculated: \begin{equation} E\left[Y_{X=0}|Z=2\right]=? \end{equation} From the SCM in the equation \eqref{SCM1}, the following SCM is got for the antecedent $X=0$: \begin{gather} X=0 \notag \newline Z=U_{2} \label{SCM1Counter2} \newline Y=3Z \notag \end{gather} The data set generated according to Table 4 and the SCM in the equation \eqref{SCM1Counter2} is shown in the Table 6. \begin{array}{ccccc} u_{2} & P\left(u_{2}\right) & x & z & y \newline 1 & \frac{1}{2} & 0 & 1 & 3 \newline 0 & \frac{1}{2} & 0 & 0 & 0 \newline \notag \end{array}
Table 6: The data set which is generated for the antecedent $X=1$ according to the Table 4 and the SCM in the equation \eqref{SCM1Counter1}.
The counterfactual expectation can then be calculated as follows: \begin{equation} E\left[Y_{X=0}|Z=2\right]=\frac{1}{2}\times 3 + \frac{1}{2} \times 0 \Rightarrow E\left[Y_{X=0}|Z=2\right]=\frac{3}{2} \end{equation}
Conclusion
In this article, it has been shown how to calculate interventional expectations and counterfactual expectations within the causal inference framework of Judea Pearl by means of an example.
References
[1] Judea Pearl, Madelyn Glymour, Nicholas P. Jewell, Causal Inference In Statistics A Primer, 2016, Wiley.
[2] Judea Pearl, Causality: Models, Reasoning and Inference, Cambridge University Press, 2009.