Introduction
First of all, this article is best viewed in Chromium and Google Chrome browsers. Some characters are not rendered correctly in Firefox. In this article, the proof of theorem about the sequential backdoor criterion is elaborated on. The theorem is given on the page 121 of [1]. Its proof is also given in the same reference.
The Sequential Backdoor Criterion
The sequential backdoor criterion gives the conditions for $P\left(y|do\left(x_{1}\right), …,do\left(x_{n}\right)\right )$ to be identifiable. $P\left(y|do\left(x_{1}\right), …,do\left(x_{n}\right)\right )$ represents the effect of the unconditional plan $\left(do\left(x_{1}\right), …,do\left(x_{n}\right)\right)$ on the variable $Y$. The sequential backdoor theorem is quoted from the page 121 of [1] as follows:
The Sequential Backdoor Criterion Theorem: The probability \begin{equation} P\left(y|do\left(x_{1}\right), … , do\left(x_{n}\right)\right) \end{equation} is identifiable if, for every $1 \leq k \leq n$, there exists a set $Z_{k}$ of covariates satisfying the following (sequential back-door) conditions: \begin{equation} Z_{k} \subseteq N_{k} \end{equation} (i.e., $Z_{k}$ consists of nondescendants of $\left \lbrace X_{k}, X_{k+1}, … , X_{n} \right \rbrace$) and \begin{equation} \left ( \left ( Y \text{ d-separated from } X_{k} \right ) \big | X_{1}, … , X_{k-1}, Z_{1}, Z_{2}, … , Z_{k} \right ) \text{ in } G_{ \underline{X}_{k}, \overline{X}_{k+1}, … , \overline{X}_{n} } \label{theSecondCond} \end{equation} When these conditions are satisfied, the effect of the plan is given by
\begin{equation} P\left(y|do\left(x_{1}\right), … , do\left(x_{n}\right)\right)=\sum_{ z_{1}, … , z_{n}}P\left(y|z_{1}, … ,z_{n}, x_{1}, … , x_{n}\right) \times \prod_{k=1}^{n} P\left(z_{k}|z_{1}, … , z_{k-1}, x_{1}, … , x_{k-1}\right) \end{equation}
Some definitions related with the theorem are to be made. The problem has a directed acyclic graph (DAG) denoted by $G$. $G$ has a vertex set $V$. $V$ is composed of four disjoint sets as follows:
1- $X$ is the set of control variables.
2- $Z$ is the set of observed variables or the covariates.
3- $U$ is the set of unobserved variables or the latent variables.
4- $Y$ is the outcome variable.
The control variables are ordered, which means that every $X_{k}$ is a nondescendant of $X_{j}$ for $j>k$. The outcome is a descendant of $X_{n}$. $N_{k}$ represents the set of covariates which are nondescendants of any variable in $\left \lbrace X_{k} , X_{k+1} , … , X_{n} \right \rbrace$.
Elaboration On The Proof
As stated in [1], the first condition to be satisfied is the following: \begin{equation} P\left ( z_{k}|z_{1}, … , z_{k-1}, x_{1}, … , x_{k-1}, \hat{x}_{k}, \hat{x}_{k+1} , … , \hat{x}_{n} \right ) = P\left ( z_{k}|z_{1}, … , z_{k-1}, x_{1}, … , x_{k-1} \right ) \label{firstCond} \end{equation} It is indicated in [1] that the relation $Z_{k} \subseteq N_{k}$ implies $Z_{k} \subseteq N_{j}$ for all $j \geq k$ and then the equality in the equation (\ref{firstCond}) is valid due to the third rule of the do-calculus since there is not a directed path from any node in $\left \lbrace Z_{1}, … , Z_{k}, X_{1}, … , X_{k-1} \right \rbrace$ to any node in $\left \lbrace X_{k}, … , X_{n} \right \rbrace$.
Let this part be elaborated on. According to the third rule of the do-calculus, the equality in the equation (\ref{firstCond}) is valid if the following d-separation condition holds: \begin{equation} \left ( \left ( Z_{k} \text{ d-separated from } \left \lbrace X_{k}, … , X_{n} \right \rbrace \right ) \big | Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right ) \text{ in } G_{\overline{\left \lbrace X_{k}, … , X_{n} \right \rbrace \left ( Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right )}} \label{dSep1} \end{equation} $\left \lbrace X_{k}, … , X_{n} \right \rbrace \left ( Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right )$ is the set of $\left \lbrace X_{k}, … , X_{n} \right \rbrace$ which are not an-ces-tors of $\left \lbrace Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right \rbrace$. It is known that $Z_{k} \subseteq N_{k}$, which means that there are no directed paths from any element in $\left \lbrace X_{k}, …,X_{n} \right \rbrace$ to $Z_{k}$. Therefore, none of $\left \lbrace X_{k}, … , X_{n} \right \rbrace$ can be an ancestor of $Z_{k}$. $Z_{k-1} \subseteq N_{k-1}$ is also valid, which means that none of $\left \lbrace X_{k-1}, X_{k}, … , X_{n} \right \rbrace$ can be an ancestor of $Z_{k-1}$. Repeating the same reasoning for $k-2, k-3, … , 1$, it can be deduced that none of $\left \lbrace X_{k}, …,X_{n} \right \rbrace$ can be an ancestor of any element in $\left \lbrace Z_{1}, Z_{2}, … , Z_{k} \right \rbrace$. The control variables are in such an order that $X_{j}$ is a nondescendant of $X_{k}$ for $j<k$. Then, there are no directed paths from any element in $\left \lbrace X_{k}, … , X_{n} \right \rbrace$ to any element in $\left \lbrace X_{1}, … , X_{k-1} \right \rbrace$. This implies that no element in $\left \lbrace X_{k}, … , X_{n} \right \rbrace$ can be an ancestor of any element in $\left \lbrace X_{1}, … , X_{k-1} \right \rbrace$. Adding the conclusion stated just a few lines ago, it can be said that no element in $\left \lbrace X_{k}, … X_{n} \right \rbrace$ can be an ancestor of any element in $\left \lbrace Z_{1}, … , Z_{k}, X_{1}, … , X_{k-1} \right \rbrace$. This result is to be often used in the rest of the article. Therefore, let it be underlined as a particular equation: \begin{equation} \text{ There cannot be a directed path from any element in } \left \lbrace X_{k}, … , X_{n} \right \rbrace \text{ to any element } \text{ in } \left \lbrace Z_{1}, … , Z_{k}, X_{1}, … , X_{k-1} \right \rbrace . \label{directedPathReq} \end{equation} Then, the following equality can be written: \begin{equation} \left \lbrace X_{k}, … , X_{n} \right \rbrace \left ( Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right )=\left \lbrace X_{k}, … , X_{n} \right \rbrace \end{equation} The condition in the equation (\ref{dSep1}) can be simplified to the following one: \begin{equation} \left ( \left ( Z_{k} \text{ d-separated from } \left \lbrace X_{k}, … , X_{n} \right \rbrace \right ) \big | Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right ) \text{ in } G_{\overline{X}_{k}, \overline{X}_{k+1}, … \overline{X}_{n}} \label{dSep1Simplified} \end{equation} Now, let it be investigated if this condition holds. Let the d-separation of $Z_{k}$ and $X_{k}$ be first examined. The d-separation of $Z_{k}$ and the other variables $X_{k+1}, … , X_{n}$ will be similar. Since $Z_{k} \subseteq N_{k}$, $Z_{k}$ is a nondescendant of $X_{k}$. There cannot be a directed path from $X_{k}$ to $Z_{k}$. If $X_{k}$ and $Z_{k}$ were to be d-connected, then the following conditions related with the paths between $Z_{k}$ and $X_{k}$ would hold:
1) The paths between $Z_{k}$ and $X_{k}$ must include at least either a fork or a collider since there cannot be a directed path from $X_{k}$ to $Z_{k}$. A chain may or may not exist in addition to a fork or a collider. All these paths must be unblocked.
2) The middle nodes of the forks cannot be from the set $\left \lbrace Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right \rbrace $ since these are conditioned on in the equation (\ref{dSep1Simplified}).
3) The edge nodes of the forks cannot be from the set $\left \lbrace X_{k}, … , X_{n} \right \rbrace$ since the condition in the equation (\ref{dSep1Simplified}) must hold in $G_{\overline{X}_{k}, \overline{X}_{k+1}, … \overline{X}_{n}}$ in which no edges can enter $\left \lbrace X_{k}, … , X_{n} \right \rbrace$.
4) The collider nodes must be from the set $\left \lbrace Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right \rbrace$ since these nodes are conditioned on in the equation (\ref{dSep1Simplified}) and unblock the colliders.
5) The inner nodes in a chain cannot be from the set $\left \lbrace Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right \rbrace$ since they are conditioned on and block the chains.
6) The inner nodes of the chains cannot be from the set $\left \lbrace X_{k}, … , X_{n} \right \rbrace$ since no edges can enter them in the graph $G_{\overline{X}_{k}, \overline{X}_{k+1}, … \overline{X}_{n}}$.
From the condition 2 and the condition 3, it can be deduced that the middle nodes of the forks must be from the set $\left \lbrace X_{k}, … , X_{n} \right \rbrace$ and the edge nodes of the forks must be from the set $\left \lbrace Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right \rbrace$. But this is in conflict with the requirement given in (\ref{directedPathReq}). As a result, there cannot be an unblocked fork between $X_{k}$ and $Z_{k}$. From the condition 4 and the requirement in (\ref{directedPathReq}), it is determined that the parent nodes of colliders cannot be from the set $\left \lbrace X_{k}, … , X_{n} \right \rbrace$. The collider node and the parent nodes of the collider can be only from the set $\left \lbrace Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right \rbrace$ provided $Z_{k} \subseteq N_{k}$ and the order in the control variables are respected. From the conditions 5 and 6, it is concluded that the inner nodes of chains can only be $Z_{k}$ as an observable variable. An unobserved variable can also be an inner node. The initial node of a chain may be a variable from $\left \lbrace X_{k}, … , X_{n} \right \rbrace$ or a variable from $\left \lbrace Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right \rbrace$ or $Z_{k}$ or an unobserved variable. The last node of a chain may be a variable from $\left \lbrace Z_{1}, … , Z_{k-1}, X_{1}, … , X_{k-1} \right \rbrace$ or $Z_{k}$ or an unobserved variable. In any case, there must be at least an unobserved variable in a chain due to the equation (\ref{directedPathReq}), the conditions 5 and 6. As a result, there can be only colliders between $X_{k}$ and $Z_{k}$ if unobserved variables are excluded for the time being. The allowed collider is shown in the Figure 1.
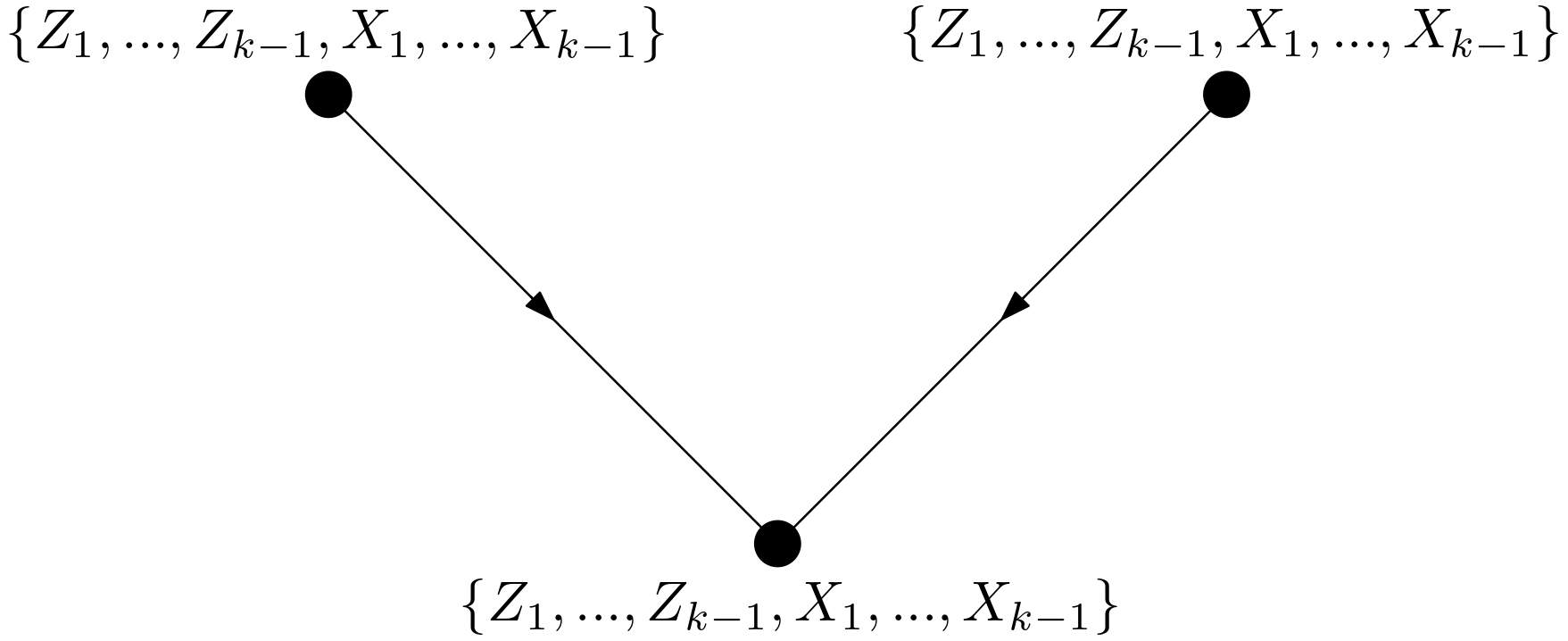
This collider can be connected to $X_{k}$ in either of the ways shown in the
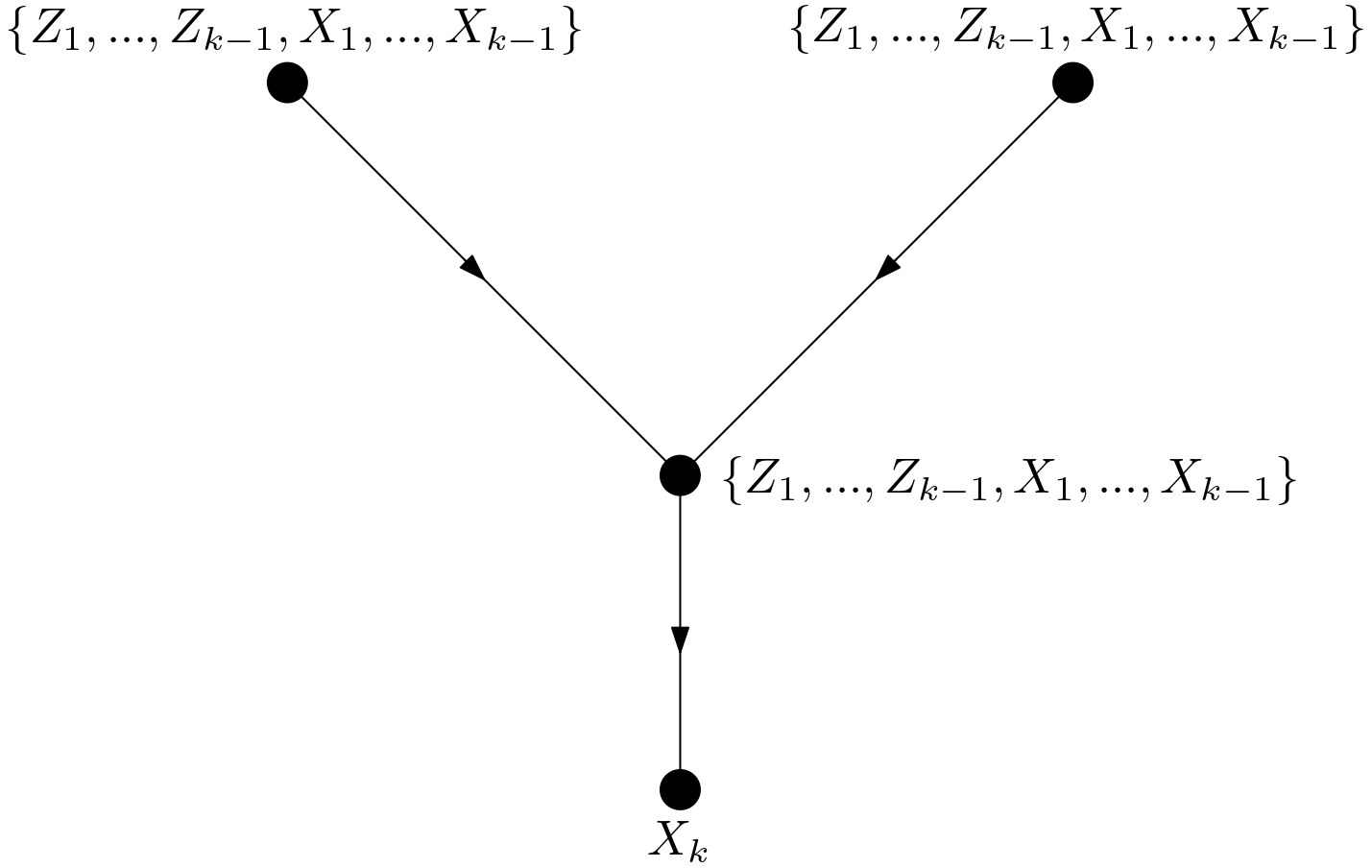
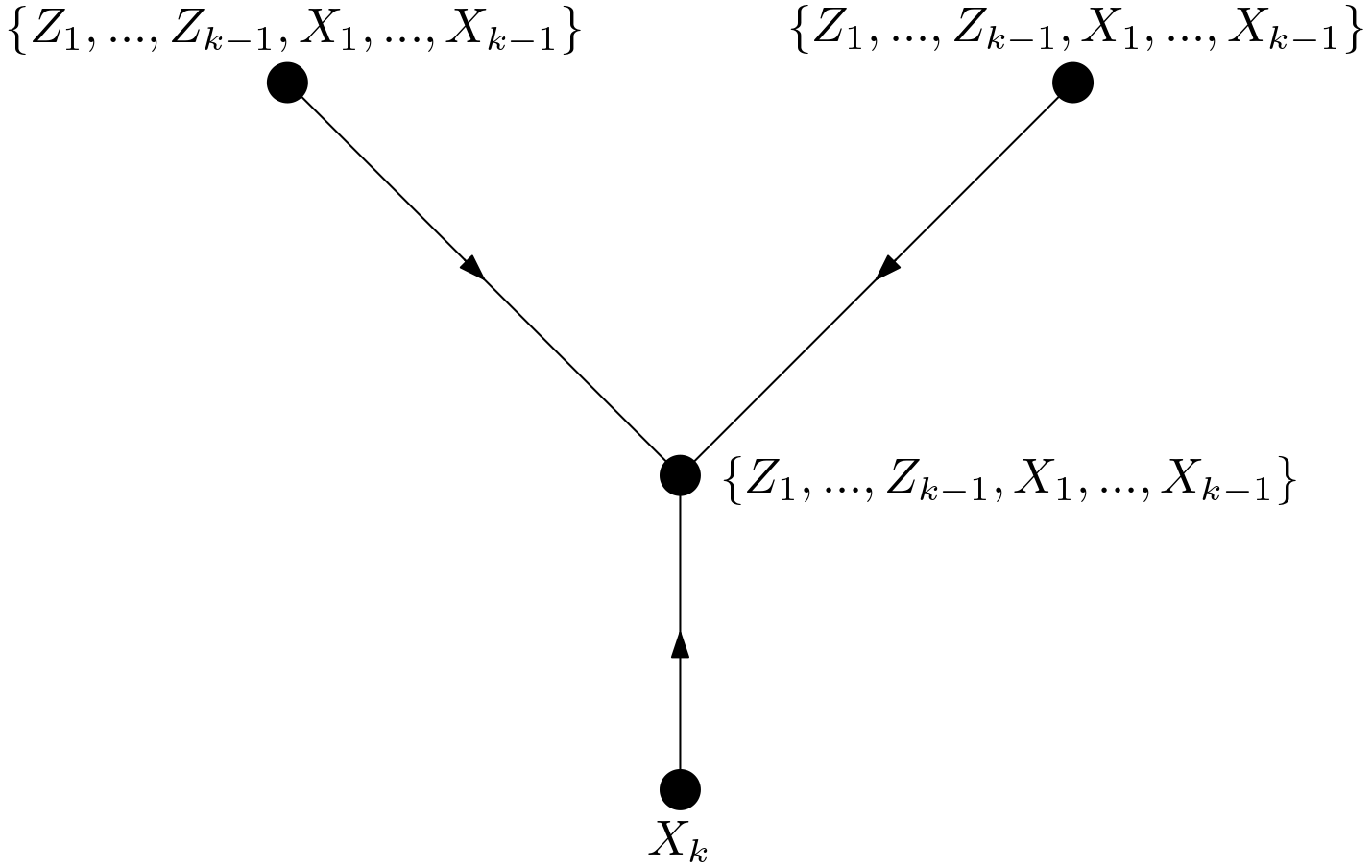
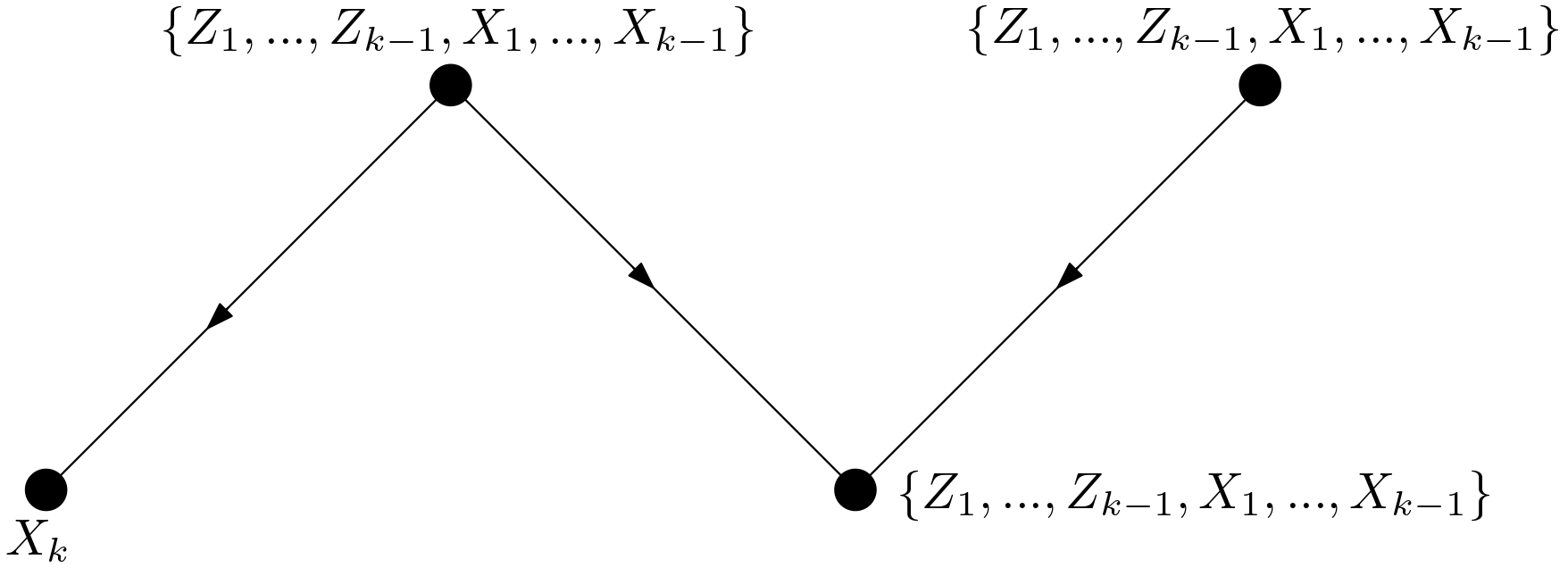
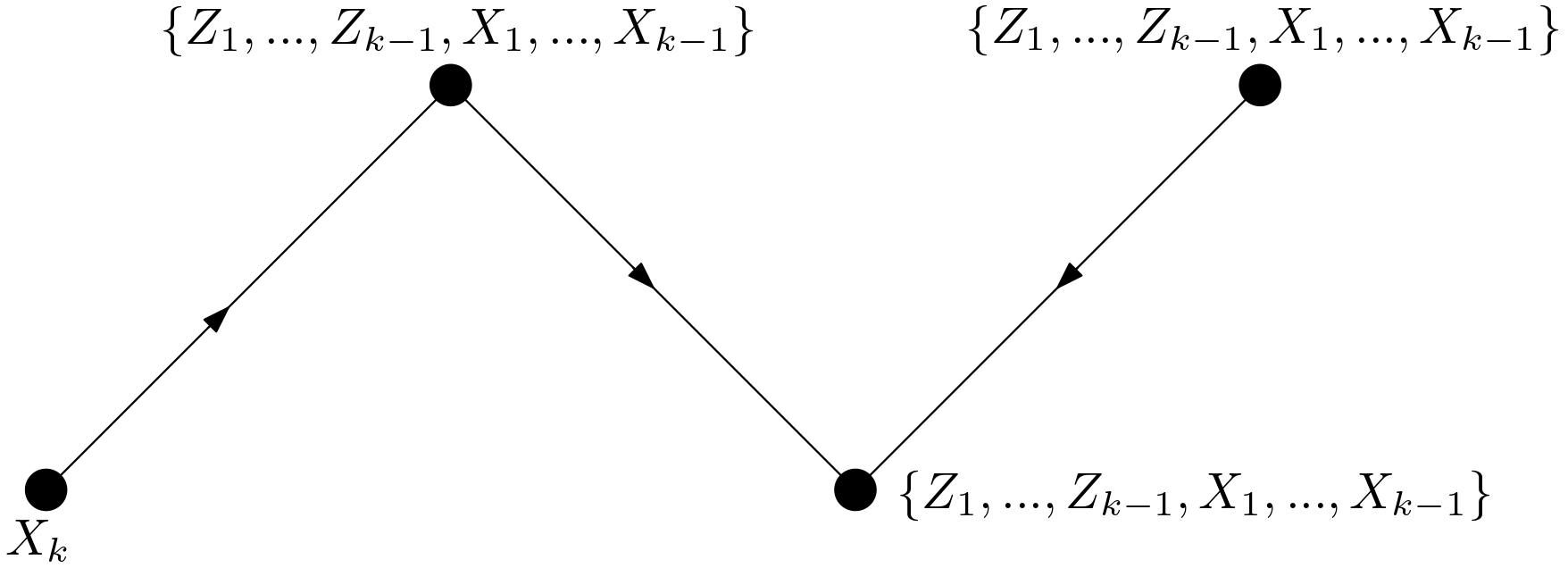
The connections in the Figures 2 and 4 are not allowed since no edges can enter $X_{k}$ in the graph $G_{\overline{X}_{k}, \overline{X}_{k+1}, … \overline{X}_{n}}$. The connections in the Figures 3 and 5 are not allowed due to the condition in the equation (\ref{directedPathReq}). Now that it has been shown that the collider in the Figure 1 cannot be connected to $X_{k}$, $Z_{k}$ and $X_{k}$ cannot be d-connected by means of a non-directed path which is made of only covariates. All the reasoning used to reach this conclusion for $Z_{k}$ and $X_{k}$ is valid also for the d-connection between $Z_{k}$ and $\left \lbrace X_{k+1}, … , X_{n} \right \rbrace$. Therefore, the d-separation condition in (\ref{dSep1}) has been proven for when the paths contain only covariates.
Now, let the cases when there are unobserved (latent) variables on the paths between $X_{k}$ and $Z_{k}$ be examined. Due to the requirement in the equation (\ref{directedPathReq}) and the conditions 2 and 3, the allowed forks with covariates and latent variables are shown in the Figure 6.

Due to the requirement in the equation (\ref{directedPathReq}) and the condition 4, the allowed colliders are given in the Figure 7.
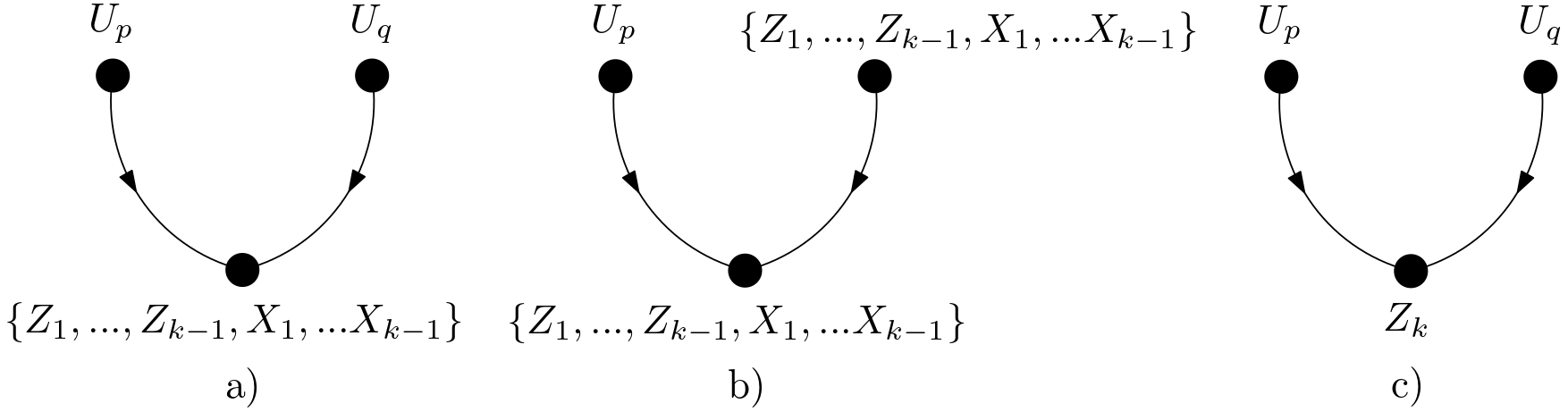
Due to the requirement in the equation (\ref{directedPathReq}) and the conditions 5 and 6, the allowed chains are shown in the Figure 8.

Since the d-separation of $Z_{k}$ and $\left \lbrace X_{k}, … , X_{n} \right \rbrace$ is examined, it is enough to go over the connections between the structures containing $\left \lbrace X_{k}, … , X_{n} \right \rbrace$ and the other allowed ones. As a reminder, the allowed structures are the ones in the Figure 1, Figure 6, Figure 7 and Figure 8.
There are two structures containing $\left \lbrace X_{k}, … , X_{n} \right \rbrace$, the one in 6a) and 8a). It is first to be examined if a valid connection can be made to the one in 6a). 6b), 6d) and 6e) cannot be connected to 6a) because the condition in the equation (\ref{directedPathReq}) is violated. The connection of 6c) to 6e) creates a blocked path due to a blocked collider. The connection of either of 7a), 7b) and 7c) to 6a) violates the condition in the equation (\ref{directedPathReq}). The connection of 8b) to 6a) creates a blocked collider and a violation of the condition in the equation (\ref{directedPathReq}). One possible connection of 8c) to 6a) creates a blocked collider and a copy of 8a). The other possible connection creates a blocked collider. One possible connection of 8d) to 6a) creates a blocked collider and the violation of the condition in the equation (\ref{directedPathReq}). The other possible connection violates the condition in the equation (\ref{directedPathReq}). One possible connection of 8e) to 6a) violates the condition the equation (\ref{directedPathReq}). The other possible connection creates a blocked collider and a violation of the condition in the equation (\ref{directedPathReq}). One possible connection of 8f) to 6a) violates the condition in the equation (\ref{directedPathReq}). The other possible connection creates a blocked collider. One possible connection of 8g) to 6a) creates a blocked collider and a copy of 8a). The other possible connection creates a blocked collider. Hence, it has been determined that none of the structures in the figures 6 and 8 can be connected to 6a) to yield an unblocked path that satisfies the condition in the equation (\ref{directedPathReq}).
Now, let the connection of 8a) to the structures in the Figures 6, 7 and 8 be examined. One possible connection of 6b) to 8a) violates the condition in the equation (\ref{directedPathReq}) and keeps 8a). The other possible connection violates the condition in the equation (\ref{directedPathReq}). One possible connection of 6c) to 8a) creates a blocked collider. The other possible connection forms a blocked collider and keeps 8a). One of the four possible connections of 6d) to 8a) creates a chain similar to 8a) and violates the condition in the equation (\ref{directedPathReq}). Another of the four possible connections creates an unblocked collider. The other one of the four possible connections creates a copy of 8a), keeps it and violates the condition in the equation (\ref{directedPathReq}). The last one of the four possible connections creates a blocked collider and keeps 8a). One possible connection of 8a) to 6e) violates the requirement in the equation (\ref{directedPathReq}). The other possible connection keeps 8a) and violates the condition in the equation (\ref{directedPathReq}). Two of the four possible connections of 8a) to 7a) are against the condition in the equation (\ref{directedPathReq}). The other two of the four possible connections keep 8a) and break the condition in the equation (\ref{directedPathReq}). One of the two possible connections of 8a) to 7b) disobeys the requirement in the equation (\ref{directedPathReq}). The other one also violates the condition in the equation (\ref{directedPathReq}) and keeps 8a). The connection of 8a) to 7c) yields the same results as the connection to 7a). One possible connection of 8a) to 8b) creates a blocked collider, keeps 8a) and 8b), creates a copy of 8c) and violates the condition in the equation (\ref{directedPathReq}). The other possible connection of 8a) to 8b) creates a blocked collider and violates the requirement in the equation (\ref{directedPathReq}). One of the four possible connections of 8a) to 8c) creates a blocked collider, keeps 8a) and 8c), creates a copy of 8a) and violates the condition in the equation (\ref{directedPathReq}). Another of the four possible connections of 8a) to 8c) creates a blocked collider, keeps 8a) and creates a chain similar to 8c). Another of the four possible connections of 8a) to 8c) creates a blocked collider, keeps 8c) and creates a chain similar to 8a). The last of the four possible connections of 8a) to 8c) creates a blocked collider. One of the four possible connections of 8a) to 8d) keeps 8a) and violates the condition in the equation (\ref{directedPathReq}). Another of the four possible connections of 8a) to 8d) keeps 8a), violates the condition in the equation (\ref{directedPathReq}), keeps 8d) and creates a chain made of three latent variables. Another of the four possible connections violates the requirement in the equation (\ref{directedPathReq}). The last of the four possible connections creates a blocked collider, keeps 8d) and violates the condition in the equation (\ref{directedPathReq}). The connection of 8a) to 8e) yields the same results as the connection to 8d). One of the four possible connections of 8a) to 8f) keeps 8a) and violates the condition in the equation (\ref{directedPathReq}). Another of the four possible connections of 8a) to 8f) creates a blocked collider, keeps 8a) and creates a chain similar to 8f). Another of the four possible connections of 8a) to 8f) violates the condition in the equation (\ref{directedPathReq}). The last one of the four possible connections of 8a) to 8f) creates a blocked collider. The connection of 8a) to 8g) yields the same results as the connection to 8c).
Therefore, it has been shown that $Z_{k}$ and $\left \lbrace X_{k}, … , X_{n} \right \rbrace $ cannot be d-connected by means of a non-directed path which contains latent variables. The elaboration for a non-directed path made of only covariates was made before this elaboration.
Since the condition in the equation (\ref{dSep1Simplified}) is the simplified form of the condition in the equation (\ref{dSep1}) which is to be satisfied for the validity of the equality in the equation (\ref{firstCond}), the elaboration on the proof of the condition in the equation (\ref{dSep1}) has now been completed.
The condition in the equation (\ref{theSecondCond}) is to be used in replacing
an intervention with an observation. The second rule of the do-calculus is in
action when replacing an intervention with an observation. Given that $G$ is
a directed acyclic graph associated with a causal model and $P$ is the probability
distribution induced by that model,
\begin{equation}
P\left ( y, | do\left(x \right ), do \left( z \right ),w \right ) =
P\left ( y, | do\left(x \right ), z, w \right ) \text{ if } \left (
\left ( Y \text{ d-separated from } Z \right ) |X, W \right )
\text{ in } G_{\overline{X} \underline{Z}}
\label{secondRule}
\end{equation}
is the second rule of the do-calculus [1].
Now, let the effect of the plan be calculated:
\begin{equation}
P \left ( y|do\left (x_{1} \right ), … , do \left (x_{n}\right )
\right ) = \sum_{z_{1}} P \left ( y,z_{1}|do\left (x_{1} \right ), …
, do \left (x_{n}\right ) \right ) \Rightarrow
\end{equation}
\begin{equation}
P \left ( y|do\left (x_{1} \right ), … , do \left (x_{n}\right )
\right ) = \sum_{z_{1}} P \left ( y|z_{1}, do\left (x_{1} \right ), …
, do \left (x_{n}\right ) \right ) P \left ( z_{1}|do\left (x_{1} \right
), … , do \left (x_{n}\right ) \right )
\label{effectPlan1}
\end{equation}
$P \left ( z_{1}|do\left (x_{1} \right ), … , do \left (x_{n}\right ) \right
)$ in the equation (\ref{effectPlan1}) can be written as $P\left (z_{1} \right )$
due to the condition in the equation (\ref{directedPathReq}). Therefore:
\begin{equation}
P \left ( y|do\left (x_{1} \right ), … , do \left (x_{n}\right )
\right ) = \sum_{z_{1}} P \left ( y|z_{1}, do\left (x_{1} \right ), …
, do \left (x_{n}\right ) \right ) P \left ( z_{1} \right )
\label{effectPlan2}
\end{equation}
Can $P \left ( y|z_{1}, do\left (x_{1} \right ), … , do \left (x_{n}\right )
\right )$ in the equation (\ref{effectPlan2}) be modified in the sense that the
intervention on $X_{1}$ is replaced with observing $X_{1}$? According to the
second rule of the do-calculus in the equation (\ref{secondRule}),
\begin{equation}
\left ( \left ( Y \text{ d-separated from } X_{1} \right )\big | Z_{1},
X_{2}, … , X_{n} \right ) \text{ in } G_{\underline{X}_{1},
\overline{X}_{2}…\overline{X}_{n}}
\label{doCalcExpansion1}
\end{equation}
is the condition to be satisfied for this replacement. Let the condition in the
equation (\ref{theSecondCond}) be rewritten:
\begin{equation}
\left(\left ( Y \text{ d-separated from } X_{k} \right )\big | X_{1},
… , X_{k-1}, Z_{1}, Z_{2}, … , Z_{k}\right) \text{ in }
G_{\underline{X}_{k}, \overline{X}_{k+1}, … , \overline{X}_{n}}
\end{equation}
For $k=1$, this condition states that
\begin{equation}
\left ( \left ( Y \text{ d-separated from } X_{1} \right )\big | Z_{1}
\right ) \text{ in } G_{\underline{X}_{1}, \overline{X}_{2}…
\overline{X}_{n}}
\label{condk=1}
\end{equation}
Is the condition in the equation (\ref{doCalcExpansion1}) the same as the one
in the equation (\ref{condk=1})? In the graph $G_{\underline{X}_{1},
\overline{X}_{2} … \overline{X}_{n}}$, there are no arrows entering $X_{2},
… X_{n}$. Therefore, they cannot be on a path between $Y$ and $X_{1}$. Then,
it does not affect the d-separability of $Y$ and $X_{1}$ whether $X_{2}, …
X_{n}$ are conditioned or not. This means that the condition in the equation
(\ref{doCalcExpansion1}) is the same as the one in the equation (\ref{condk=1}).
Hence, the expansion in the equation (\ref{effectPlan2}) can be
simplified to the following:
\begin{equation}
P \left ( y|do\left (x_{1} \right ), … , do \left (x_{n}\right )
\right ) = \sum_{z_{1}} P \left ( y|z_{1}, x_{1} ,do \left (x_{2} \right
) , … , do \left (x_{n} \right ) \right ) P \left ( z_{1} \right )
\end{equation}
After the simplification, the expansion continues and $P \left ( y|z_{1}, x_{1}
, … , do \left (x_{n} \right ) \right )$ is written using the total probabilty
rule with the expansion over $Z_{2}$:
\begin{equation}
P \left ( y|do\left (x_{1} \right ), … , do \left (x_{n}\right )
\right ) = \sum_{z_{1}} \left (\sum_{z_{2}} P \left ( y, z_{2}|z_{1},
x_{1}, do\left(x_{2} \right ), … , do \left (x_{n}\right ) \right )
\right ) P \left ( z_{1} \right ) \Rightarrow
\end{equation}
\begin{equation}
P \left ( y|do\left (x_{1} \right ), … , do \left (x_{n}\right )
\right ) = \sum_{z_{1}} \left (\sum_{z_{2}} P \left ( y| z_{2}, z_{1},
x_{1}, do\left ( x_{2}\right ), … , do \left (x_{n}\right ) \right )
P \left ( z_{2}| z_{1},x_{1} ,do \left (x_{2} \right ), … , do \left
(x_{n}\right ) \right ) \right ) P \left ( z_{1} \right )
\label{effectPlan3}
\end{equation}
$P \left ( z_{2}| z_{1},x_{1} ,do \left (x_{2} \right ), … , do \left (x_{n}
\right ) \right )$ in the equation (\ref{effectPlan3}) can be written as
$P \left ( z_{2}| z_{1},x_{1}\right )$ due to the requirement in the equation
(\ref{directedPathReq}). Therefore:
\begin{equation}
P \left ( y|do\left (x_{1} \right ), … , do \left (x_{n}\right )
\right ) = \sum_{z_{1}} \left (\sum_{z_{2}} P \left ( y| z_{2}, z_{1},
x_{1}, do\left ( x_{2}\right ), … , do \left (x_{n}\right ) \right )
P \left ( z_{2}| z_{1},x_{1} \right ) \right ) P \left ( z_{1} \right )
\Rightarrow
\end{equation}
\begin{equation}
P \left ( y|do\left (x_{1} \right ), … , do \left (x_{n}\right )
\right ) = \sum_{z_{1}} \sum_{z_{2}} P \left ( y| z_{2}, z_{1},
x_{1}, do\left ( x_{2}\right ), … , do \left (x_{n}\right ) \right )
P \left ( z_{2}| z_{1},x_{1} \right ) P \left ( z_{1} \right )
\label{effectPlan4}
\end{equation}
Can the intervention on $X_{2}$ in $P \left ( y| z_{2}, z_{1}, x_{1}, do\left
( x_{2}\right ), … , do \left (x_{n}\right ) \right )$ in the equation
(\ref{effectPlan4}) be replaced with observing $X_{2}$? This question can again
be answered using the second rule of the do-calculus given in the equation
(\ref{secondRule}). According to this rule, the following condition must be
satisfied for the replacement to be valid:
\begin{equation}
\left ( \left ( Y \text{ d-separated from } X_{2} \right )\big | Z_{2},
Z_{1},X_{1}, X_{3}, … , X_{n} \right ) \text{ in } G_{\underline{X}_{2},
\overline{X}_{3}…\overline{X}_{n}}
\label{doCalcExpansion2}
\end{equation}
The condition in the equation (\ref{theSecondCond}) implies the following for
$k=2$:
\begin{equation}
\left ( \left ( Y \text{ d-separated from } X_{2} \right )\big | X_{1},
Z_{1}, Z_{2} \right ) \text{ in } G_{\underline{X}_{2}, \overline{X}_{3}…
\overline{X}_{n}}
\label{condk=2}
\end{equation}
Since there are no arrows entering $X_{3}, … , X_{n}$ in the DAG
$G_{\underline{X}_{2}, \overline{X}_{3}… \overline{X}_{n}} $, a path on which
either of $X_{3}, … , X_{n}$ exists is not possible from $Y$ to $X_{2}$. Then,
the condition in the equation (\ref{doCalcExpansion2}) is the same as the one in
the equation (\ref{condk=2}). Hence, the replacement of the intervention on
$X_{2}$ with observing $X_{2}$ can be made to yield the following:
\begin{equation}
P \left ( y|do\left (x_{1} \right ), … , do \left (x_{n}\right )
\right ) = \sum_{z_{1}} \sum_{z_{2}} P \left ( y| z_{2}, z_{1},
x_{1}, do\left ( x_{2}\right ), … , do \left (x_{n}\right ) \right )
P \left ( z_{2}| z_{1},x_{1} \right ) P \left ( z_{1} \right ) \Rightarrow
\end{equation}
\begin{equation}
P \left ( y|do\left (x_{1} \right ), … , do \left (x_{n}\right )
\right ) = \sum_{z_{1}} \sum_{z_{2}} P \left ( y| z_{2}, z_{1},
x_{1}, x_{2},do \left ( x_{3} \right ) … , do \left (x_{n}\right )
\right ) P \left ( z_{2}| z_{1},x_{1} \right ) P \left ( z_{1} \right )
\end{equation}
Repating similar operations for $k=3,…,n$, the following expression which is free of interventions is obtained at last: \begin{equation} P \left ( y|do\left (x_{1} \right ), … , do \left (x_{n}\right ) \right ) = \sum_{z_{n}} … \sum_{z_{2}} \sum_{z_{1}} P \left (y|z_{1}, … , z_{n}, x_{1}, … , x_{n} \right ) \times P\left (z_{1} \right )P\left (z_{2}|z_{1}, x_{1} \right ) … P\left (z_{n}|z_{1}, x_{1}, z_{2}, x_{2}, … , z_{n-1}, x_{n-1} \right ) \end{equation}
Conclusion
Some elaboration has been made on the proof of the sequential backdoor criteriron.
References
[1] Judea Pearl, Causality: Models, Reasoning and Inference, Cambridge University Press, 2009.