Introduction
First of all, this article is best viewed in Chromium and Google Chrome browsers. Some characters are not rendered correctly in Firefox. In this article, a calculation of a direct controlled effect is made. The relations between the post-intervention and pre-inervention probabilities are explained in a detailed manner. The DAG of the causal model is the same as that of the causal model given in section 3.7 of [1].
The Controlled Direct Effect
It is assumed that there is a causal model with the features $X$, $Y$, $Z$ and $I$. The DAG of the causal model is given in the Figure 1.
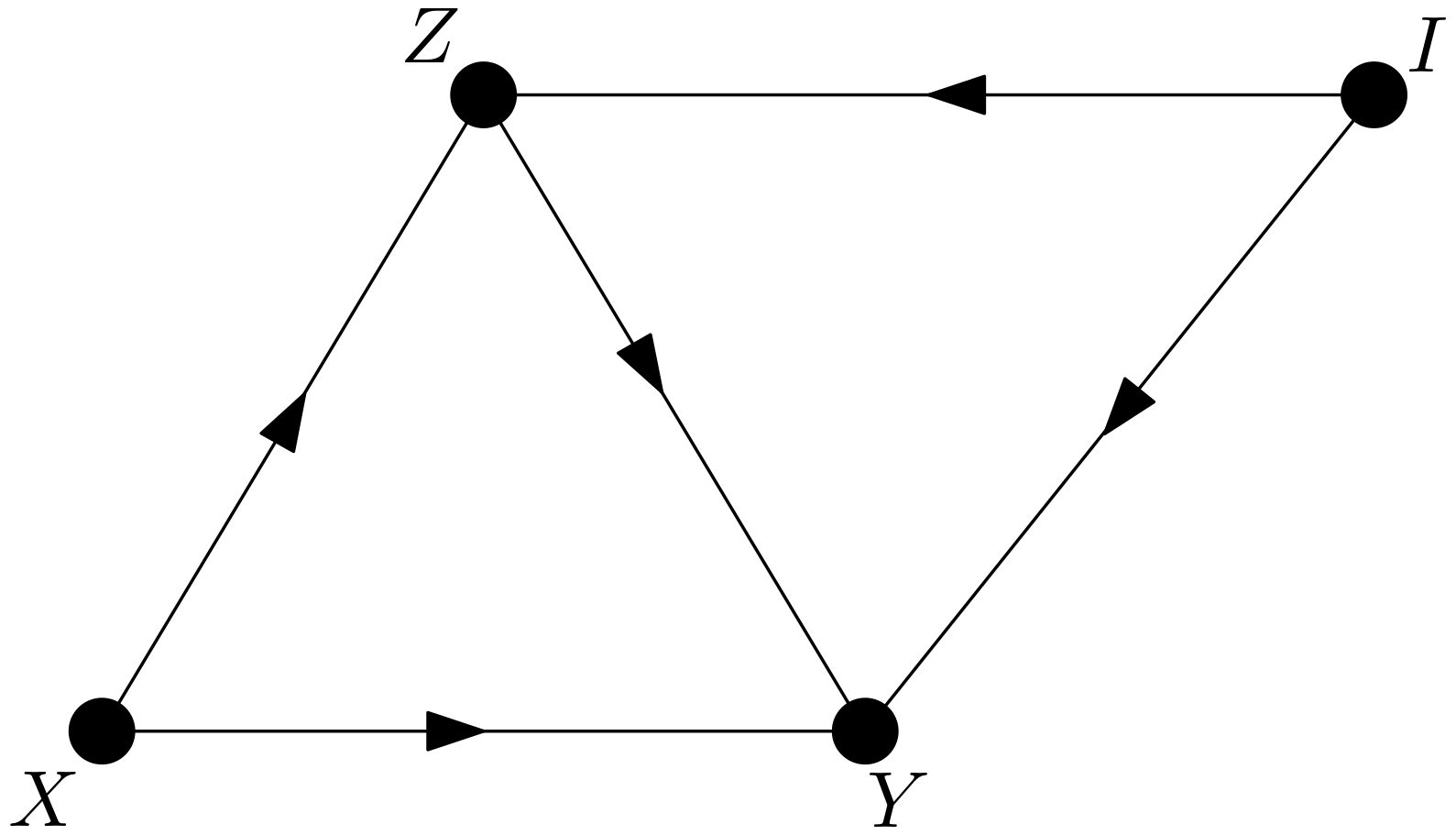
The aim is to calculate the controlled direct effect of $X$ on $Y$. There are two directed paths from $X$ to $Y$. One of them is $X \rightarrow Y$ and the other is $X \rightarrow Z \rightarrow Y$. $Z$ is a mediating variable. The controlled direct effect of $X$ on $Y$ is defined as follows: \begin{equation} CDE = p\left(y|do\left(x\right), do\left(z\right)\right)-p\left(y|do\left(x^{\prime}\right),do\left(z\right)\right) \end{equation} Let the intervention on $X$ in $p\left(y|do\left(x\right), do\left(z\right)\right)$ be dealt with first. The rules of do-calculus will be used in this task. Can the intervention be converted to an observation? That is the mean, is $p\left(y|do\left(x\right), do\left(z\right)\right)$ equal to $p\left(y|x, do\left(z\right)\right)$? For this equality to hold, $X$ and $Y$ must be conditionally independent given $Z$ in the graph $G_{\underline{X}\overline{Z}}$. $G_{\underline{X}\overline{Z}}$ is shown in the Figure 2.
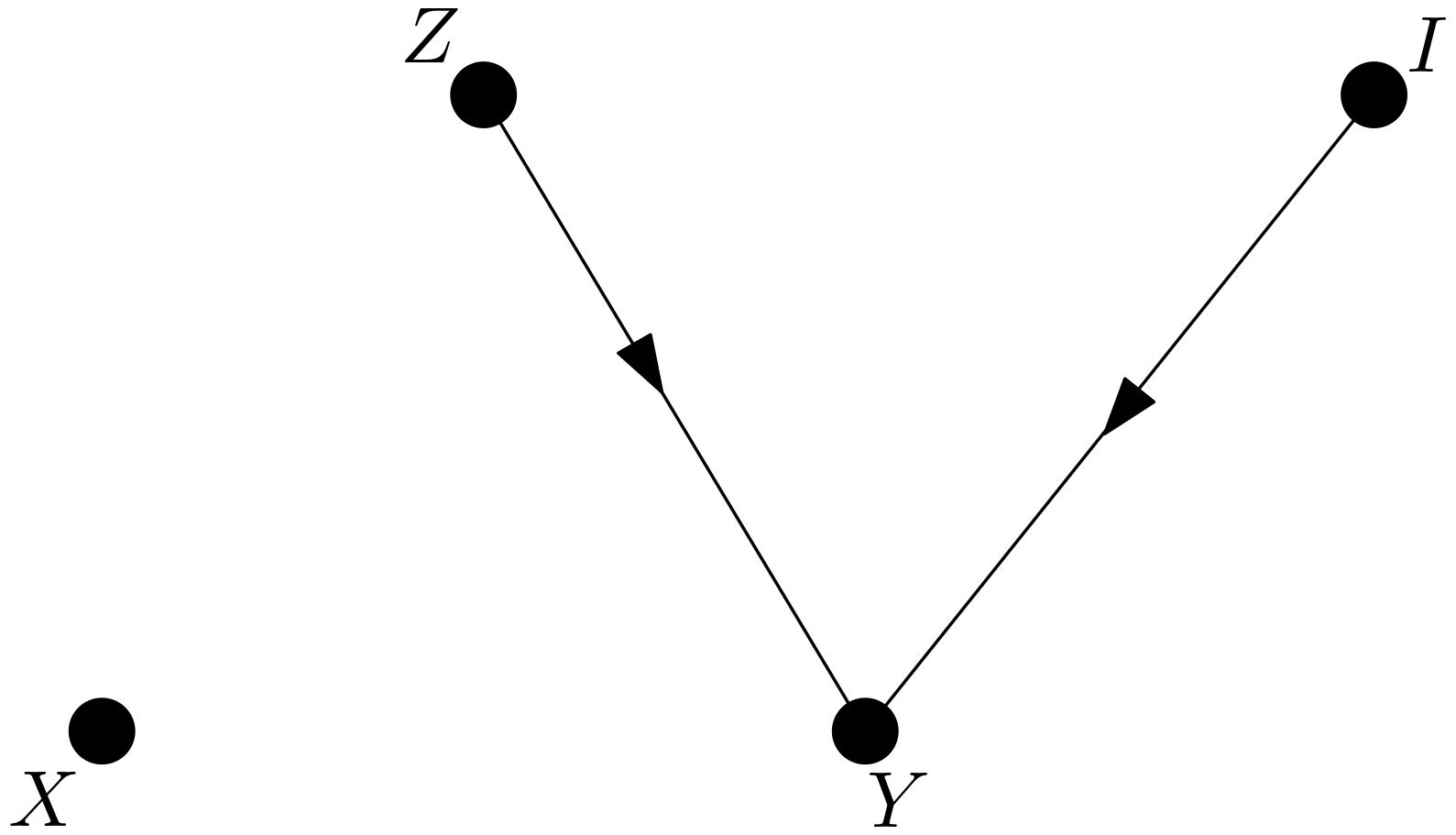
As can be seen from the Figure 2, $X$ and $Y$ are conditionally independent given $Z$. Therefore, the following equality can safely be written: \begin{equation} p\left(y|do\left(x\right), do\left(z\right)\right)=p\left(y|x, do\left(z\right)\right) \end{equation} Now, it is time to consider the intervention on $Z$. In calculating $p\left(y|x, do\left(z\right)\right)$, the manipulated graph is first drawn. It is $G_{\overline{Z}}$. The graph $G_{\overline{Z}}$ is shown in the Figure 3.
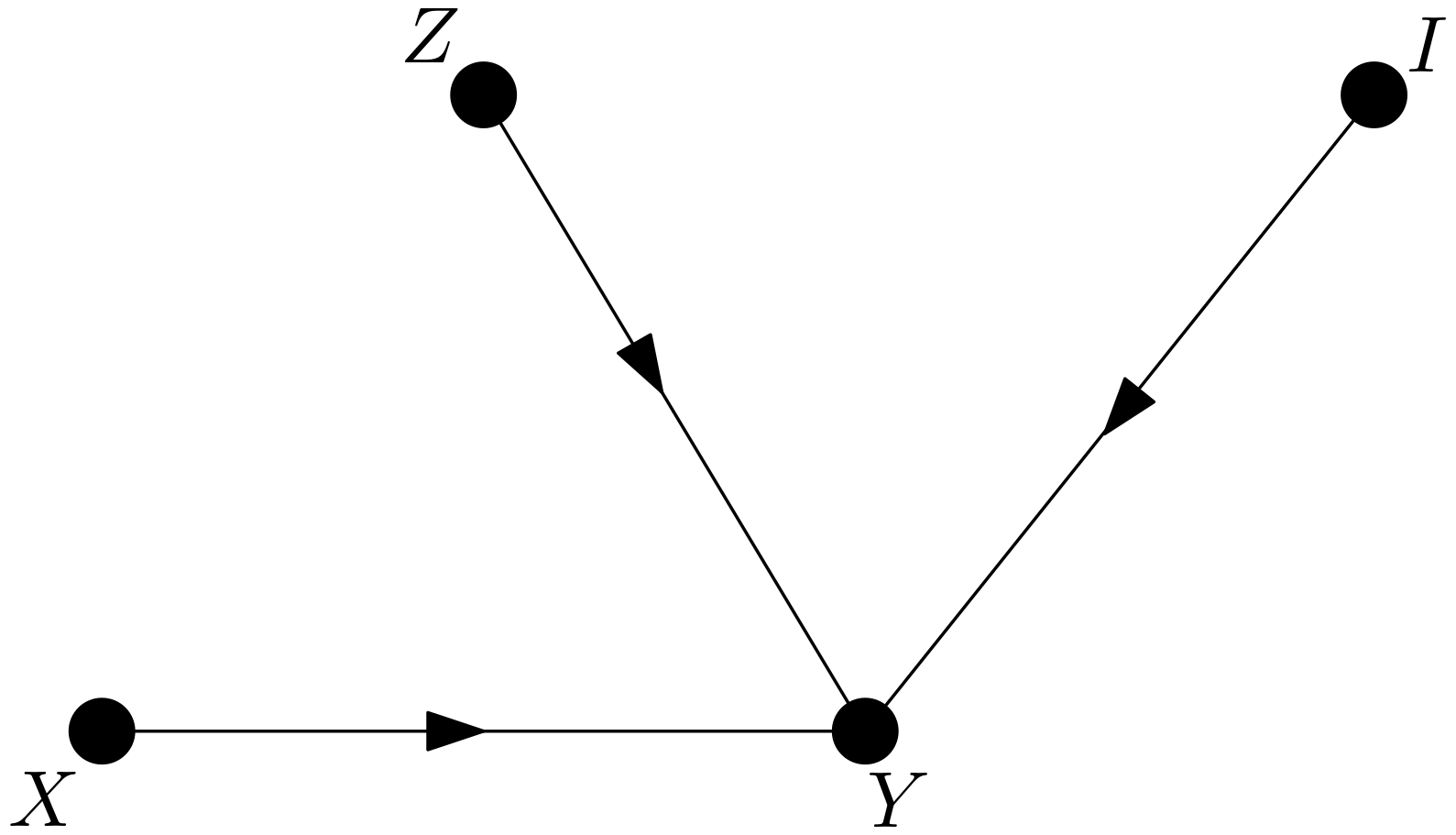
Let the probability distribution represented by this graph be denoted by $p_{m}$. $p\left(y|x, do\left(z\right)\right)$ can be written as follows, which is nothing but the law of total probability: \begin{equation} p\left(y|x, do\left(z\right)\right)=\sum_{i}p_{m}\left(y|x,z,i\right)p_{m}\left(i|x,z\right) \label{adjustment} \end{equation} Let $p_{m}\left(i|x,z\right)$ first be written in terms of pre-intervention probabilities. According to the graph in the Figure 3, $I$ and $X$ are d-separated due to the collider $X \rightarrow Y \leftarrow I$. $I$ and $Z$ are also d-separated due to the collider $Z \rightarrow Y \leftarrow I$. Then, $I$ must be independent of both of $X$ and $Z$, which implies the following equality: \begin{equation} p_{m}\left(i|x,z\right)=p_{m}(i) \end{equation} Due to the autonomous mechanisms in the causal model, removing the edges entering $Z$ from the original graph does not affect the mechanism generating $I$. Hence: \begin{equation} p_{m}(i) = p(i) \end{equation} Let $p_{m}\left(y|x,z,i\right)$ be examined now. First, the paths between $Y$ and $X$ in the original graph and in $G_{\overline{Z}}$ are to be considered. In the original graph, the paths between $Y$ and $X$ are $X \rightarrow Z \rightarrow Y$, $X \rightarrow Z \leftarrow I \rightarrow Y$ and $X \rightarrow Y$. $X \rightarrow Z \rightarrow Y$ is blocked due to conditioning on $Z$. $X \rightarrow Z \leftarrow I \rightarrow Y$ is blocked due to conditioning on $I$. The only connection between $Y$ and $X$ is the path $X \rightarrow Y$ in the original graph. It is the only connection between $Y$ and $X$ in $G_{\overline{Z}}$, as well. The mechanism represented by the edge $X \rightarrow Y$ in the original graph and the mechanism denoted by $X \rightarrow Y$ in $G_{\overline{Z}}$ are the same due to autonomy.
Second, the paths between $Y$ and $Z$ in the original graph and in $G_{\overline{Z}}$ are to be considered. In the original graph, the paths between $Y$ and $Z$ are $Y \leftarrow X \rightarrow Z$, $Y \leftarrow I \rightarrow Z$ and $Z \rightarrow Y$. The path $Y \leftarrow X \rightarrow Z$ is blocked due to conditioning on $X$. The path $Y \leftarrow I \rightarrow Z$ is blocked due to conditioning on $I$. The only connection between $Y$ and $Z$ is the path $Z \rightarrow Y$. It is the only connection between $Y$ and $Z$ in $G_{\overline{Z}}$, as well. The mechanism represented by the edge $Z \rightarrow Y$ in the original graph and the mechanism denoted by $Z \rightarrow Y$ in $G_{\overline{Z}}$ are the same due to autonomy.
Third, the paths between $Y$ and $I$ in the original graph and in $G_{\overline{Z}}$ are to be considered. In the original graph, the paths between $Y$ and $I$ are $Y \leftarrow X \rightarrow Z \leftarrow I$, $Y \leftarrow Z \leftarrow I$ and $I \rightarrow Y$. The path $Y \leftarrow X \rightarrow Z \leftarrow I$ is blocked due to conditioning on $X$. The path $Y \leftarrow Z \leftarrow I$ is blocked due to conditioning on $Z$. The only connection between $Y$ and $I$ is the path $I \rightarrow Y$. It is the only connection between $Y$ and $I$ in $G_{\overline{Z}}$, as well. The mechanism represented by the edge $I \rightarrow Y$ in the original graph and the mechanism denoted by $I \rightarrow Y$ in $G_{\overline{Z}}$ are the same due to autonomy.
The previous three explanations imply the following equality: \begin{equation} p_{m}\left(y|x,z,i\right) = p\left(y|x,z,i\right) \end{equation} The expression in the equation (\ref{adjustment}) can now be written in terms of pre-intervention probabilities: \begin{equation} p\left(y|x, do\left(z\right)\right)=\sum_{i}p\left(y|x,z,i\right)p\left(i\right) \end{equation} Therefore, the controlled direct effect of $X$ on $Y$ is expressed in terms of pre-intervention probabilities as follows: \begin{equation} CDE = \sum_{i}p\left(y|x,z,i\right)p\left(i\right)-\sum_{i}p\left(y|x^{\prime},z,i\right)p\left(i\right) \Rightarrow \end{equation} \begin{equation} CDE = \sum_{i}\left[p\left(y|x,z,i\right)-p\left(y|x^{\prime},z,i\right)\right]p\left(i\right) \label{cde_expansion} \end{equation} This expression is in compliance with the backdoor criterion. There is no backdoor path from $X$ to $Y$, which implies that there is no need to make an adjustment for the intervention on $X$. There are two backdoor paths from $Z$ to $Y$. The first one is $Z \leftarrow X \rightarrow Y$. This path is blocked due to conditioning on $X$. The second one is $Y \leftarrow I \rightarrow Z$. This path can be blocked by conditioning on $I$, which means that an adjustment for $I$ must be made. This adjustment is just the one implemented in the equation (\ref{cde_expansion}).
Conclusion
A calculation for a direct controlled effect has been made. The relations between the post-intervention and pre-inervention probabilities have been explained in a detailed way.
References
[1] Judea Pearl, Madelyn Glymour, Nicholas P. Jewell, Causal Inference In Statistics A Primer, John Wiley and Sons Ltd., 2016.