Introduction
In this article, the calculation of causal effects of conditional interventions is demonstrated on an example. The causal model in this example is the one in the study question 3.5.1 in [1].
The Conditional Intervention
The directed acyclic graph (DAG) of the causal model is given in the Figure 1.
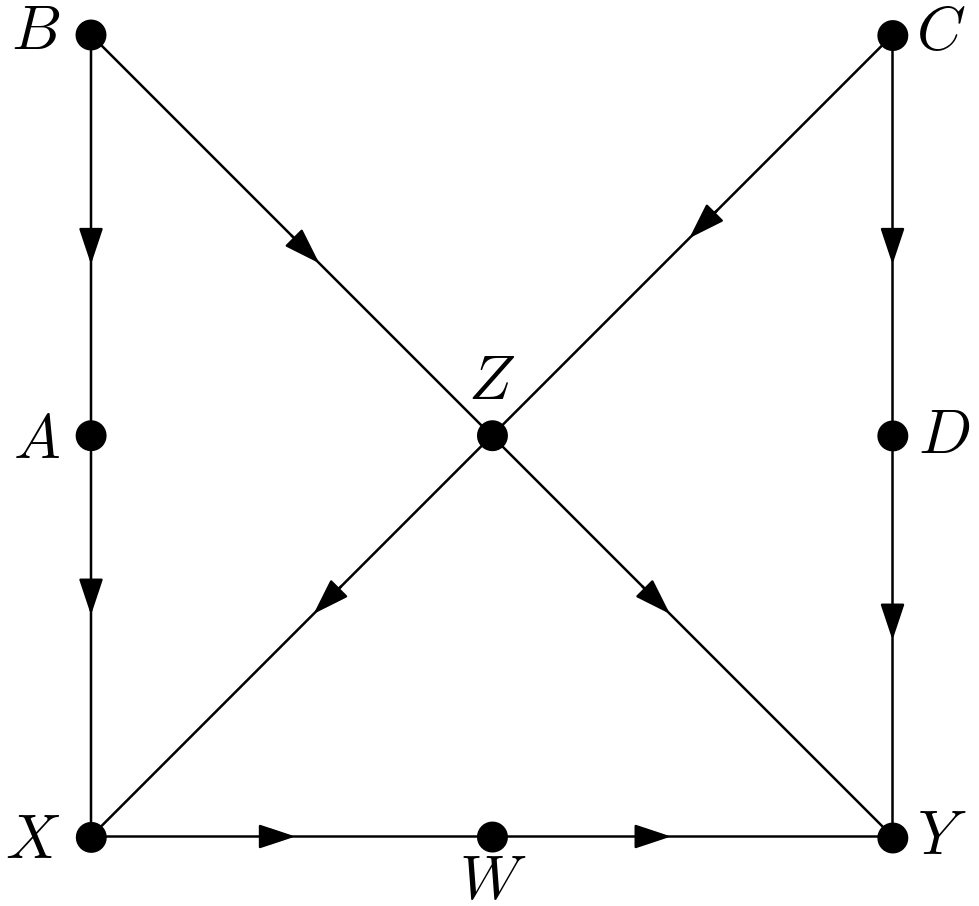
The $z$-specific causal effect of $X$ on $Y$ is to be calculated in a detailed manner. The adjective “$z$-specific” means that the causal effect of $X$ on $Y$ is to be found for a specific $z$ value of $Z$.
The backdoor criterion is to be used to find the minimal adjustment sets. All of the adjustment sets must contain $Z$ since an intervention conditioned on $Z$ is being done. The backdoors from $X$ to $Y$ are as follows: \begin{equation} 1) X \leftarrow Z \rightarrow Y \end{equation} \begin{equation} 2) X \leftarrow Z \leftarrow C \rightarrow D \rightarrow Y \end{equation} \begin{equation} 3) X \leftarrow A \leftarrow B \rightarrow Z \rightarrow Y \end{equation} \begin{equation} 4) X \leftarrow A \leftarrow B \rightarrow Z \leftarrow C \rightarrow D \rightarrow Y \end{equation} The first, the second and the third ones are blocked by conditioning on $Z$. Con-di-tion-ing on $Z$ unblocks the collider in the fourth one. Hence, one of $A, B, C$ and $D$ must also be conditioned on to block the fourth backdoor. As a result, the minimal adjustment sets are as follows: \begin{equation} 1) A, Z \ 2) B, Z \ 3) C, Z \ 4) D, Z \end{equation}
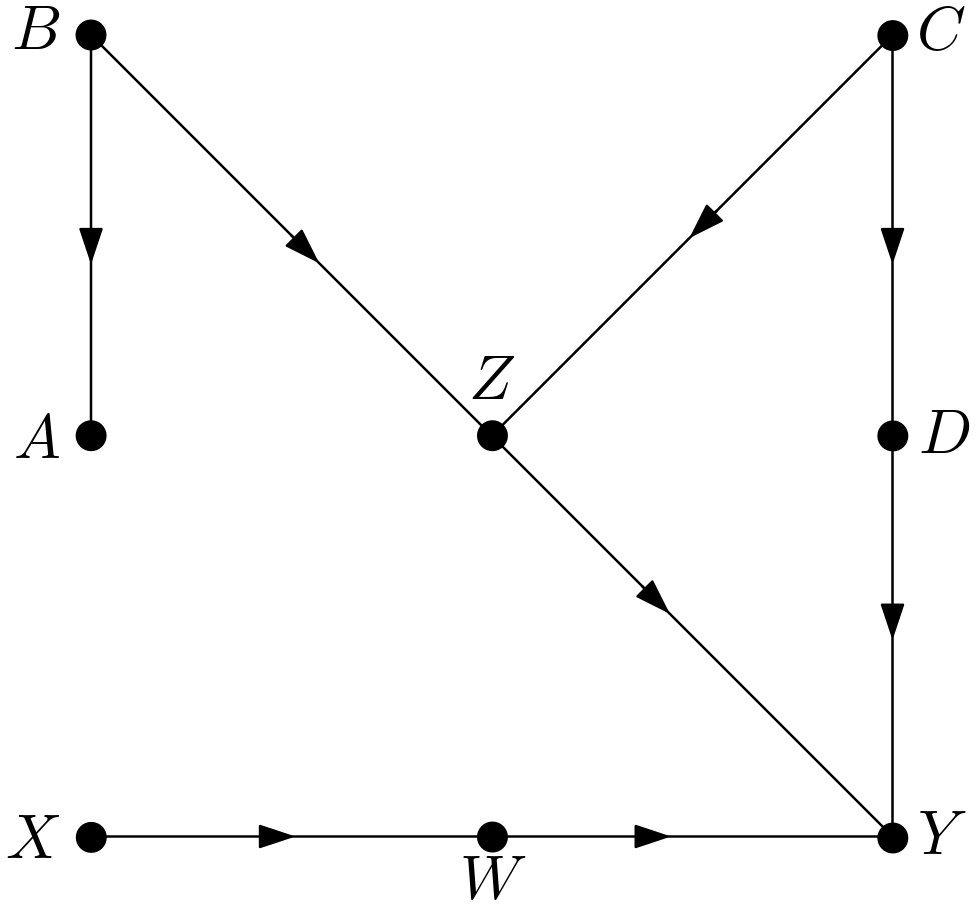
Let the $z$-specific causal effect of $X$ on $Y$ be calculated using the first adjustment set. This causal quantity can be calculated as follows: \begin{equation} p\left(y|do\left(x\right), z\right)=\sum_{a} p_{m} \left(y|x, z, a\right)p_{m}\left(a|x,z\right) \label{adjustment1} \end{equation} $p_{m}$ denotes the manipulated probability distribution which is valid for the ma-nip-u-lated graph shown in the Figure 2. Let $p_{m} \left(y|x, z, a\right)$ be examined. In the manipulated graph, the edges entering $X$ are all removed. Hence, there are no backdoor paths from $X$ to $Y$ in the manipulated graph. All of the backdoor paths from $X$ to $Y$ are blocked in the original graph. In addition, removing the edges entering $X$ does not change the rest of the mechanisms in the graph due to the autonomy property. Therefore, the following equality can be written: \begin{equation} p_{m} \left(y|x, z, a\right)=p \left(y|x, z, a\right) \end{equation} As to $p_{m}\left(a|x,z\right)$, first of all, it can be seen from the manipulated graph that $A$ and $X$ are conditionally independent given $Z$. Hence, the following equality is true: \begin{equation} p_{m}\left(a|x,z\right)=p_{m}\left(a|z\right) \end{equation} Let the reasons of this conditional independence be stated. The path $A \leftarrow B \rightarrow Z \rightarrow Y \leftarrow W \leftarrow X$ is blocked by conditioning on $Z$ or by the collider $W \rightarrow Y \leftarrow Z$. The path $A \leftarrow B \rightarrow Z \leftarrow C \rightarrow D \rightarrow Y \leftarrow W \leftarrow X$ is blocked by the collider $D \rightarrow Y \leftarrow W$.
For the calculation of $p_{m}\left(a|z\right)$, the paths between $A$ and $Z$ in the manipulated graph must be compared to the paths between $A$ and $Z$ in the original graph. In both of the graphs, the path $A \leftarrow B \rightarrow Z$ is unblocked. In the original graph, the path $A \rightarrow X \leftarrow Z$ is blocked since there is no conditioning on $X$. In the manipulated graph, this path is removed, which means that there is not a connection between $A$ and $Z$ through this path, either. In the original graph, the path $A \rightarrow X \rightarrow W \rightarrow Y \leftarrow Z$ is blocked due to the collider $W \rightarrow Y \leftarrow Z$. In the manipulated graph, the path $A \rightarrow X$ is removed, which means that there is no connection between $A$ and $Z$ through $A \rightarrow X \rightarrow W \rightarrow Y \leftarrow Z $. In the original graph, $A \rightarrow X \rightarrow W \rightarrow Y \leftarrow D \leftarrow C \rightarrow Z$ is blocked due to the collider $W \rightarrow Y \leftarrow D$. In the manipulated graph, the path $A \rightarrow X$ is removed, which means that there is not a connection between $A$ and $Z$ through $A \rightarrow X \rightarrow W \rightarrow Y \leftarrow D \leftarrow C \rightarrow Z$. After comparing all of the paths between $A$ and $Z$, it has been determined they are in the same states from the perspective of being blocked. With the autonomy of the mechanisms in the model added, the following is valid: \begin{equation} p_{m}\left(a|z\right)=p\left(a|z\right) \end{equation} The expression written in terms of the post-intervention probabilities in the equa-tion (\ref{adjustment1}) can now be written in terms of the pre-intervention probabilities as follows: \begin{equation} p\left(y|do\left(x\right), z\right)=\sum_{a} p \left(y|x, z, a\right)p\left(a|z\right) \end{equation}
Let the $z$-specific causal effect of $X$ on $Y$ be calculated using the second adjustment set. The adjustment expression is as follows: \begin{equation} p \left(y|do\left(x\right),z\right) = \sum_{b} p_{m}\left(y|x,z,b\right)p_{m} \left(b|x,z\right) \label{adjustment2} \end{equation} In order to calculate $p_{m}\left(y|x,z,b\right)$, the manipulated graph and the original graph are compared with the conditions on $X$, $Z$ and $B$. In the manipulated graph, the directed edges entering $X$ are removed and in this way, all of the backdoors from $X$ to $Y$ disappear. In the original graph, conditioning on $Z$ and $B$ blocks all of the backdoor paths from $X$ to $Y$. Hence, along with the inclusion of the autonomy of the mechanisms, $p_{m}\left(y|x,z,b\right)$ must be equal to $p\left(y|x,z,b\right)$: \begin{equation} p_{m}\left(y|x,z,b\right)=p\left(y|x,z,b\right) \end{equation} As for $p_{m} \left(b|x,z\right)$, it can be seen in the manipulated graph that $B$ and $X$ are conditionally d-separated given $Z$. This implies the following equality: \begin{equation} p_{m} \left(b|x,z\right)=p_{m} \left(b|z\right) \end{equation} The reasons of this conditional d-separation are to be mentioned. The path $B \rightarrow Z \rightarrow Y \leftarrow W \leftarrow X$ is blocked by either conditioning on $Z$ or the collider $Z \rightarrow Y \leftarrow W$. The path $B \rightarrow Z \leftarrow C \rightarrow D \rightarrow Y \leftarrow W \leftarrow X$ is blocked by the collider $D \rightarrow Y \leftarrow W$. What is $p_{m} \left(b|z\right)$? In order to answer this question, the paths between $B$ and $Z$ in the manipulated graph must be compared to the ones between $B$ and $Z$ in the original graph. In the original graph, the path $B \rightarrow A \rightarrow X \leftarrow Z$ is blocked by the collider $A \rightarrow X \leftarrow Z$. In the manipulated graph, $A \rightarrow X$ and $Z \rightarrow X$ are removed. Hence, this path does not exist in the original graph and the manipulated graph and the original graph are the same from the perspective of the path $B \rightarrow A \rightarrow X \leftarrow Z$. The path $B \rightarrow A \rightarrow X \rightarrow W \rightarrow Y \leftarrow Z$ in the original graph is blocked by the collider $W \rightarrow Y \leftarrow Z$. Since $A \rightarrow X$ is removed in the manipulated graph, this path does not exist in the manipulated graph. Therefore, the two graphs are the same from the perspective of the path $B \rightarrow A \rightarrow X \rightarrow W \rightarrow Y \leftarrow Z$. In the original graph, the path $B \rightarrow A \rightarrow X \rightarrow W \rightarrow Y \leftarrow D \leftarrow C \rightarrow Z$ is blocked by the collider $W\rightarrow Y\leftarrow D$. The path $A \rightarrow X$ is removed in the manipulated graph. Hence, the two graphs are the same as each other from the perspective of this path. Since the manipulated and the original graph are the same as each other from the perspectives of the paths between $B$ and $Z$ and the mechanisms in both of the graphs are the same due to autonomy, $p_{m}\left(b|z\right)$ must be equal to $p\left(b|z\right)$: \begin{equation} p_{m}\left(b|z\right)=p\left(b|z\right) \end{equation} Now, the post-intervention probabilities in the equation (\ref{adjustment2}) can be written in terms of pre-intervention probabilities to obtain the following result: \begin{equation} p\left(y|do\left(x\right),z\right)=\sum_{b} p\left(y|x,z,b\right)p\left(b|z\right) \end{equation}
Let the $z$-specific causal effect of $X$ on $Y$ be calculated using the third ad-just-ment set. The adjustment equation can be written as follows: \begin{equation} p\left(y|do\left(x\right),z\right)=\sum_{c} p_{m}\left(y|x,z,c\right)p_{m}\left(c|x,z\right) \label{adjustment3} \end{equation} $p_{m}\left(y|x,z,c\right)$ is to be converted to a pre-intervention probability. In order to achieve this conversion, the manipulated graph and the original graph is examined for the backdoors from $X$ to $Y$. In the manipulated graph, $A \rightarrow X$ and $Z \rightarrow X$ are removed. Hence, there are no backdoor paths from $X$ to $Y$ in the manipulated graph. In the original graph, all of the backdoor paths from $X$ to $Y$ are blocked due to conditining on $Z$ and $C$. The manipulated and the original graph are the same as each other from the perspective of backdoors. The mechanisms in the manipulated graph are the same as the ones in the original graph due to autonomy. Then, the following equality can be written: \begin{equation} p_{m}\left(y|x,z,c\right) = p\left(y|x,z,c\right) \end{equation} It is the turn of $p_{m}\left(c|x,z\right)$. From the manipulated graph in the Figure 2, it can be discovered that $C$ and $X$ are conditionally independent given $Z$: \begin{equation} p_{m}\left(c|x,z\right)=p_{m}\left(c|z\right) \end{equation} The path $C \rightarrow Z \rightarrow Y \leftarrow W \leftarrow X$ is blocked by $Z$ or the collider $Z \rightarrow Y \leftarrow W$. The path $C \rightarrow D \rightarrow Y \leftarrow W \leftarrow X$ is blocked by the collider $D \rightarrow Y \leftarrow W$. That’s why $C$ and $X$ are conditionally independent given $Z$. How can $p_{m}\left(c|z\right)$ be expressed in terms of pre-intervention probabilities? In order to answer this question, the paths between $C$ and $Z$ in the manipulated graph and the original graph must be compared. The path $C \rightarrow D \rightarrow Y \leftarrow Z$ is blocked by the collider $D \rightarrow Y \leftarrow Z$ in the original graph. This path is also blocked by the same collider in the manipulated graph, as well. The path $C \rightarrow D \rightarrow Y \leftarrow W \leftarrow X \leftarrow Z$ is blocked by the collider $D \rightarrow Y \leftarrow W$ in the original graph. The path $X \leftarrow Z$ is removed in the manipulated graph. Hence, the same situation exists for the two graphs from the perspective of this path. The path $C \rightarrow D \rightarrow Y \leftarrow W \leftarrow X \leftarrow A \leftarrow B \rightarrow Z$ is blocked by the collider $D \rightarrow Y \leftarrow W$. The path $X \leftarrow A$ is removed in the manipulated graph. Therefore, the two graphs are equivalent two each other from the perspective of this path. The autonomy and the fact that the paths between $C$ and $Z$ have been observed to be in the same states of being blocked imply the following equality: \begin{equation} p_{m}\left(c|z\right)=p\left(c|z\right) \end{equation}
As a result, the adjustment formula in the equation (\ref{adjustment3}) can be written in terms of the pre-intervention probabilities as follows: \begin{equation} p\left(y|do\left(x\right),z\right)=\sum_{c} p\left(y|x,z,c\right)p\left(c|z\right) \end{equation}
The $z$ specific causal effect of $X$ on $Y$ is to be calculated using the last adjustment set. The adjustment equation is given by the following: \begin{equation} p\left(y|do\left(x\right),z\right)=\sum_{d}p_{m}\left(y|x,z,d\right)p_{m}\left(d|x,z\right) \label{adjustment4} \end{equation} In order to convert $p_{m}\left(y|x,z,d\right)$ to an expression in terms of the pre-intervention probabilities, the backdoor paths between $X$ and $Y$ in the manipulated and the original graph must be compared. In the manipulated graph, all of the paths entering $X$ are removed. Hence, there are no backdoor paths from $X$ to $Y$ in the manipulated graph. In the original graph, due to conditioning on $Z$ and $D$, all of the backdoor paths from $X$ to $Y$ are blocked. With the autonomy in mind, it can be concluded that the two graphs are the same as each other when the paths between $X$ and $Y$ are considered. Hence, the following equality can safely be written: \begin{equation} p_{m}\left(y|x,z,d\right)=p\left(y|x,z,d\right) \end{equation}
As to $p_{m}\left(d|x,z\right)$, the first thing to notice is that $X$ and $D$ are conditionally independent given $Z$. In the manipulated graph, the path $D \rightarrow Y \leftarrow W \leftarrow X$ is blocked by the collider $D \rightarrow Y \leftarrow W$ and the path $D \leftarrow C \rightarrow Z \rightarrow Y \leftarrow W \leftarrow X$ is blocked by $Z$ or the collider $Z \rightarrow Y \leftarrow W$. From these observations, it can be seen that $X$ and $D$ are conditionally independent given $Z$: \begin{equation} p_{m}\left(d|x,z\right)=p_{m}\left(d|z\right) \end{equation} In order to write $p_{m}\left(d|z\right)$ in terms of the pre-intervention probabilities, the paths between $D$ and $Z$ must be examined in both of the manipulated and the original graphs. In the original graph, $D \leftarrow C \rightarrow Z$ is not blocked. In the manipulated graph, this path is not blocked, either. The path $D \rightarrow Y \leftarrow Z$ is blocked since the collision node $Y$ is not conditioned on in the original graph. In the manipulated graph, the same situation is valid. In the original graph, $D \rightarrow Y \leftarrow W \leftarrow X \leftarrow Z$ is blocked by the collider $D\rightarrow Y \leftarrow W$. The path $Z \rightarrow X$ is removed in the manipulated graph. Hence, there is not a dependence between $D$ and $Z$ through this path in the manipulated graph, either. In the original graph, the path $D \rightarrow Y \leftarrow W \leftarrow X \leftarrow A \leftarrow B \rightarrow Z$ is blocked by the collider $D \rightarrow Y \leftarrow W$. In the manipulated graph, the path $A \rightarrow X$ is removed. Hence, there is not a dependence between $D$ and $Z$ through this path in the manipulated graph, either. With the autonomy in mind, these observations imply the following equality: \begin{equation} p_{m}\left(d|z\right)=p\left(d|z\right) \end{equation}
The relation in the equation (\ref{adjustment4}) can now be written in terms of the pre-intervention probabilities: \begin{equation} p\left(y|do\left(x\right),z\right)=\sum_{d}p\left(y|x,z,d\right)p\left(d|z\right) \end{equation}
Conclusion
A conditional intervention problem has been solved in a detailed manner.
References
[1] Judea Pearl, Madelyn Glymour, Nicholas P. Jewell, Causal Inference In Statistics A Primer, John Wiley and Sons Ltd., 2016.