Introduction
In this article, the constant error carrousel is examined. The constant error carrousel is the basic building block of a long short term memory cell discovered by [1].
Definition
The constant error carrousel is a structure to achieve constant error gradient as its name implies. It contains a single unit connected to itself. The unrolled form of the CEC is given in the Figure 1. $w$ and $g$ are to be found in the following section.
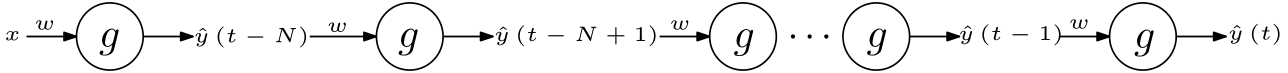
$g$ is the activation function of the CEC. It must be the identity function, $g\left(x\right)=x$, and the coefficient $w$ must be $1$ for keeping the error gradient constant. $\hat{y}\left(t\right)$ is the output at time $t$. $y$ is the target to be reached.
Derivation
The activation function of the CEC and the value of the constant $w$ is to be found in this section. \begin{equation} \hat{y}\left(t-N+1\right)=g\left(w\hat{y}\left(t-N\right)\right) \Rightarrow \text{loss}\left(t-N+1\right)=\frac{1}{2} \left(y-\hat{y}\left(t-N+1\right)\right)^{2} \Rightarrow \end{equation} \begin{equation} \frac{\partial \text{loss}\left(t-N+1\right)}{\partial w}=\left(y-\hat{y}\left(t-N+1\right)\right)\left(-1\right)\frac{\partial \hat{y}\left(t-N+1\right)}{\partial w} \Rightarrow \end{equation} \begin{equation} \frac{\partial \text{loss}\left(t-N+1\right)}{\partial w}=\left(y-\hat{y}\left(t-N+1\right)\right)\left(-1\right)\frac{\partial g\left(w\hat{y}\left(t-N\right)\right)}{\partial w} \Rightarrow \end{equation} \begin{equation} \frac{\partial \text{loss}\left(t-N+1\right)}{\partial w}=\left(y-\hat{y}\left(t-N+1\right)\right)\left(-1\right)\frac{\partial g\left(w\hat{y}\left(t-N\right)\right)}{\partial \left(w\hat{y}\left(t-N\right)\right)}\frac{\partial \left(w\hat{y}\left(t-N\right)\right)}{\partial w} \Rightarrow \end{equation} \begin{equation} \frac{\partial \text{loss}\left(t-N+1\right)}{\partial w}=\left(y-\hat{y}\left(t-N+1\right)\right)\left(-1\right)g^{\prime}\left(\hat{y}\left(t-N\right)\right)\hat{y}\left(t-N\right) \end{equation} The error gradient at time $t-N+1$ has been calculated. Now, let it be calculated for the instant $t-N+2$. \begin{equation} \hat{y}\left(t-N+2\right)=g\left(w\hat{y}\left(t-N+1\right)\right) \Rightarrow \text{loss}\left(t-N+2\right)=\frac{1}{2} \left(y-\hat{y}\left(t-N+2\right)\right)^{2} \Rightarrow \end{equation} \begin{equation} \frac{\partial \text{loss}\left(t-N+2\right)}{\partial w}=\left(y-\hat{y}\left(t-N+2\right)\right)\left(-1\right)\frac{\partial \hat{y}\left(t-N+2\right)}{\partial w} \Rightarrow \end{equation} \begin{equation} \frac{\partial \text{loss}\left(t-N+2\right)}{\partial w}=\left(y-\hat{y}\left(t-N+2\right)\right)\left(-1\right)\frac{\partial g\left(w\hat{y}\left(t-N+1\right)\right)}{\partial w} \Rightarrow \end{equation} \begin{equation} \frac{\partial \text{loss}\left(t-N+2\right)}{\partial w}=\left(y-\hat{y}\left(t-N+2\right)\right)\left(-1\right)\frac{\partial g\left(w\hat{y}\left(t-N+1\right)\right)}{\partial \left(w\hat{y}\left(t-N+1\right)\right)}\frac{\partial \left(w\hat{y}\left(t-N+1\right)\right)}{\partial w} \Rightarrow \end{equation} \begin{equation} \frac{\partial \text{loss}\left(t-N+2\right)}{\partial w}=\left(y-\hat{y}\left(t-N+2\right)\right)\left(-1\right)g^{\prime}\left(\hat{y}\left(t-N+1\right)\right)\hat{y}\left(t-N+1\right) \end{equation} The aim is to make the error gradients at these two instants to be equal: \begin{equation} \frac{\partial \text{loss}\left(t-N+1\right)}{\partial w}=\frac{\partial \text{loss}\left(t-N+2\right)}{\partial w} \Rightarrow \end{equation} \begin{equation} \left(y-\hat{y}\left(t-N+1\right)\right)\left(-1\right)g^{\prime}\left(\hat{y}\left(t-N\right)\right)\hat{y}\left(t-N\right)= \end{equation} \begin{equation} \left(y-\hat{y}\left(t-N+2\right)\right)\left(-1\right)g^{\prime}\left(\hat{y}\left(t-N+1\right)\right)\hat{y}\left(t-N+1\right) \Rightarrow \end{equation} \begin{equation} \left(y-\hat{y}\left(t-N+1\right)\right)g^{\prime}\left(\hat{y}\left(t-N\right)\right)\hat{y}\left(t-N\right)= \end{equation} \begin{equation} \left(y-w\hat{y}\left(t-N+1\right)\right)g^{\prime}\left(w\hat{y}\left(t-N\right)\right)w\hat{y}\left(t-N\right) \Rightarrow \end{equation} \begin{equation} \left(y-\hat{y}\left(t-N+1\right)\right)g^{\prime}\left(\hat{y}\left(t-N\right)\right)=\left(y-w\hat{y}\left(t-N+1\right)\right)g^{\prime}\left(w\hat{y}\left(t-N\right)\right)w \label{constantGrad} \end{equation} The equation (\ref{constantGrad}) is satisfied if $g$ is chosen to be the identity function and $w$ to be equal to $1$. If $g$ is the identity function, then its derivative is $1$. After replacing $w$ with $1$, the following equality is obtained: \begin{equation} \left(y-\hat{y}\left(t-N+1\right)\right)=\left(y-\hat{y}\left(t-N+1\right)\right) \end{equation}
Conclusion
The activation function and the $w$ coefficient for the constant error carrousel (CEC) which is the basic building block of an LSTM cell have been derived.
References
[1] Sepp Hochreiter and Jurgen Schmidhuber. Long Short-Term Memory. Neural Computation, 9(8):1735–1780, November 1997.